正确率40.0%某堆雪在融化过程中,其体积$${{V}}$$(单位:$${{m}^{3}{)}}$$与融化时间$${{t}}$$(单位:$${{h}{)}}$$近似满足函数关系$$V ( t )=H \bigg( 1 0-\frac{1} {1 0} t \bigg)^{3} ( H$$为常数$${{)}}$$,其图象如图所示.记此堆雪从融化开始到结束的平均融化速度为$${{v}{¯}{,}}$$那么瞬时融化速度等于$${{v}{¯}}$$的时刻是图中的()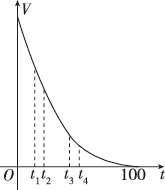
C
A.$${{t}_{1}}$$
B.$${{t}_{2}}$$
C.$${{t}_{3}}$$
D.$${{t}_{4}}$$
2、['瞬时变化率']正确率60.0%一质点运动的方程为$$s=5-3 t^{2},$$若该质点在时间段$$[ 1, ~ 1+\Delta t ]$$内相应的平均速度为$$- 3 \Delta t-6,$$则该质点在$${{t}{=}{1}}$$时的瞬时速度是()
D
A.$${{−}{3}}$$
B.$${{3}}$$
C.$${{6}}$$
D.$${{−}{6}}$$
3、['瞬时变化率']正确率60.0%已知函数$${{f}{(}{x}{)}}$$满足$$f ( 1 )=-1, \, \, f^{\prime} ( 1 )=2.$$则函数$$y=f ( x ) \cdot\mathrm{e}^{x}$$在$${{x}{=}{1}}$$处的瞬时变化率为()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{e}}$$
D.$${{2}{e}}$$
4、['简单复合函数的导数', '瞬时变化率']正确率60.0%随着科学技术的发展,放射性同位素技术已经广泛应用于医学、航天等众多领域,并取得了显著的经济效益,假设在某放射性同位素的衰变过程中,其含量$${{N}}$$(单位:贝克)与时间$${{t}}$$(单位:天)满足函数关系$$N ( t )=N_{0} 2^{-\frac{t} {2 4}} \,,$$其中$${{N}_{0}}$$为$${{t}{=}{0}}$$时该放射性同位素的含量.已知$${{t}{=}{{2}{4}}}$$时,该放射性同位素含量的瞬时变化率为$$- 8 \mathrm{l n} 2,$$则$$N ( 9 6 )=$$()
C
A.$${{1}{2}}$$
B.$${{1}{2}{{l}{n}}{2}}$$
C.$${{2}{4}}$$
D.$${{2}{4}{{l}{n}}{2}}$$
5、['瞬时变化率']正确率60.0%质点沿直线运动的路程$${{s}}$$$${{(}}$$单位:$${{m}{)}}$$与时间$${{t}}$$$${{(}}$$单位:$${{s}{)}}$$的关系式是$${{s}{=}{^{5}\sqrt {t}}{,}}$$则质点在$${{t}{=}{4}{s}}$$时的瞬时速度为()
B
A.$$\frac{1} {2 \sqrt{2^{3}}} \mathrm{m / s}$$
B.$$\frac{1} {1 0 \sqrt{2^{3}}} \mathrm{m} / \mathrm{s}$$
C.$${\frac{2} {5}} \sqrt{2^{3}} \, \mathrm{m / s}$$
D.$${\frac{1} {1 0}} \sqrt{2^{3}} \mathrm{m / s}$$
6、['瞬时变化率']正确率60.0%若某物体做直线运动,路程$${{S}}$$$${{(}}$$单位:$${{m}{)}}$$与时间$${{t}}$$$${{(}}$$单位:$${{s}{)}}$$的关系由函数$$S ( t )=k \cdot\mathrm{e}^{-\frac{t} {2}}$$表示.当$${{t}{=}{2}{s}}$$时,该物体的瞬时速度$${{v}}$$为$$- \frac{2} {\mathrm{e}} ~ \mathrm{m / s},$$则当$${{t}{=}{6}{s}}$$时,该物体行驶的路程为()
D
A.$$2 \mathrm{e}^{-6} \mathrm{~ m}$$
B.$$4 \mathrm{e}^{-6} \mathrm{~ m}$$
C.$$\mathrm{2 e^{-3} ~ m}$$
D.$$4 \mathrm{e}^{-3} \ \mathrm{m}$$
7、['导数的几何意义', '瞬时变化率']正确率60.0%一个质量$$m=5 ~ \mathrm{k g}$$的物体做直线运动,运动距离$${{s}}$$$${{(}}$$单位:$${{m}{)}}$$与时间$${{t}}$$(单位:$${{s}{)}}$$的关系可用函数$$s ( t )=t+\frac{1} {2} t^{2}$$表示,并且物体的动能$$E_{k}={\frac{1} {2}} m v^{2} ( m$$为物体质量$${,{v}}$$为物体运动速度$${{)}}$$,则物体开始运动后第$${{7}{s}}$$时的动能是()
A
A.$${{1}{6}{0}{J}}$$
B.$${{1}{6}{5}{J}}$$
C.$${{1}{7}{0}{J}}$$
D.$${{1}{7}{5}{J}}$$
8、['函数图象的识别', '导数的几何意义', '瞬时变化率']正确率40.0%如图所示,一质点$$P \left( \begin{matrix} {x, \ y} \\ \end{matrix} \right)$$在$${{x}{O}{y}}$$平面上沿曲线运动,速度大小不变,其在$${{x}}$$轴上的投影点$$Q \ ( \textbf{x}, \textbf{0} )$$的运动速度$$V=V \left( t \right)$$的图象大致为()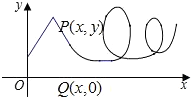
B
A.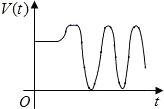
B.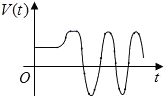
C.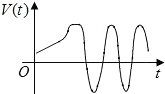
D.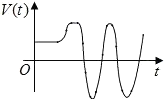
正确率60.0%$${{−}}$$个物体的运动方程为$$s=1-t+t^{2},$$其中$${{s}}$$的单位是米,$${{t}}$$的单位是秒,那么物体在$${{5}}$$秒末的瞬时速度是()
D
A.$${{6}}$$米$${{/}}$$秒
B.$${{7}}$$米$${{/}}$$秒
C.$${{8}}$$米$${{/}}$$秒
D.$${{9}}$$米$${{/}}$$秒
10、['导数的概念', '基本初等函数的导数', '瞬时变化率', '导数的几何意义']正确率60.0%已知某质点的位移$${{s}}$$与移动时间$${{t}}$$满足$$s=t^{2} \cdot e^{t-2}$$,则质点在$${{t}{=}{2}}$$的瞬时速度是()
C
A.$${{4}}$$
B.$${{6}}$$
C.$${{8}}$$
D.$${{1}{6}}$$
1. 首先计算平均融化速度 $$ \overline{v} $$:雪完全融化时 $$ V(t) = 0 $$,解得 $$ t = 100 $$ 小时。初始体积 $$ V(0) = H \times 10^3 = 1000H $$,平均速度为 $$ \overline{v} = \frac{1000H - 0}{100} = 10H $$。瞬时速度为 $$ V'(t) = -3H \times \frac{1}{10} \left(10 - \frac{t}{10}\right)^2 $$。设瞬时速度等于平均速度,即 $$ -3H \times \frac{1}{10} \left(10 - \frac{t}{10}\right)^2 = 10H $$,解得 $$ t = 50 $$ 小时,对应图中的 $$ t_2 $$。答案为 B。
2. 瞬时速度为平均速度的极限,当 $$ \Delta t \to 0 $$ 时,$$ -3 \Delta t - 6 \to -6 $$。答案为 D。
3. 计算 $$ y = f(x) \cdot e^x $$ 的导数:$$ y' = f'(x) \cdot e^x + f(x) \cdot e^x $$。在 $$ x = 1 $$ 处,$$ y'(1) = f'(1) \cdot e + f(1) \cdot e = 2e - e = e $$。答案为 C。
4. 首先求导数 $$ N'(t) = N_0 \cdot 2^{-\frac{t}{24}} \cdot (-\frac{1}{24} \ln 2) $$。当 $$ t = 24 $$ 时,$$ N'(24) = -8 \ln 2 $$,解得 $$ N_0 = 192 $$。代入 $$ t = 96 $$,得 $$ N(96) = 192 \times 2^{-4} = 12 $$。答案为 A。
5. 路程函数 $$ s = t^{1/5} $$,瞬时速度 $$ v = \frac{ds}{dt} = \frac{1}{5} t^{-4/5} $$。在 $$ t = 4 $$ 时,$$ v = \frac{1}{5} \times 4^{-4/5} = \frac{1}{10 \sqrt{2^3}} $$。答案为 B。
6. 速度函数为 $$ v(t) = S'(t) = -\frac{k}{2} e^{-t/2} $$。当 $$ t = 2 $$ 时,$$ v(2) = -\frac{k}{2} e^{-1} = -\frac{2}{e} $$,解得 $$ k = 4 $$。路程 $$ S(6) = 4 e^{-3} $$。答案为 D。
7. 速度函数 $$ v(t) = s'(t) = 1 + t $$。当 $$ t = 7 $$ 时,$$ v(7) = 8 $$,动能 $$ E_k = \frac{1}{2} \times 5 \times 8^2 = 160 $$。答案为 A。
8. 由于质点速度大小不变,投影点 $$ Q $$ 的速度 $$ V(t) $$ 会随曲线斜率变化而变化,表现为非匀速运动,且速度方向会反转。选项中只有 B 符合这种变化规律。
9. 速度函数 $$ v(t) = s'(t) = -1 + 2t $$。当 $$ t = 5 $$ 时,$$ v(5) = 9 $$。答案为 D。
10. 计算导数 $$ s'(t) = 2t e^{t-2} + t^2 e^{t-2} $$。在 $$ t = 2 $$ 时,$$ s'(2) = 4 + 4 = 8 $$。答案为 C。
.jpg)