.jpg)
正确率80.0%若$$f ( x )=\operatorname{l n} (-x )，$$则$$f^{\prime} (-2 0 2 4 )=$$（）
A
A.$$- \frac1 {2 0 2 4}$$
B.$${{−}{{2}{0}{2}{4}}}$$
C.$$\frac{1} {2 0 2 4}$$
D.$${{2}{0}{2}{4}}$$
2、['简单复合函数的导数'， '二项式系数和与各项的系数和']正确率40.0%若$$( 3 x-1 )^{5}=a_{0}+a_{1} x+a_{2} x^{2}+\dots$$$${{+}{{a}_{5}}{{x}^{5}}{，}}$$则$$a_{1}+2 a_{2}+3 a_{3}+4 a_{4}+5 a_{5}=$$（）
D
A.$${{8}{0}}$$
B.$${{1}{2}{0}}$$
C.$${{1}{8}{0}}$$
D.$${{2}{4}{0}}$$
3、['简单复合函数的导数'， '导数的四则运算法则'， '基本初等函数的导数']正确率60.0%已知函数$$f ( x )=2^{x}+\operatorname{l o g}_{2} x，$$则$$f^{\prime} ( 1 )=$$（）
B
A.$${{3}}$$
B.$$2 \mathrm{l n} 2+\frac{1} {\mathrm{l n} 2}$$
C.$$2 \mathrm{l n} 2+1$$
D.$$2+\frac{1} {\mathrm{l n} 2}$$
4、['简单复合函数的导数'， '导数的四则运算法则']正确率80.0%函数$$f ( x )=( x+2 a ) ( x-a )^{2}$$的导函数为（）
C
A.$$f^{\prime} ( x )=2 ( x^{2}-a^{2} )$$
B.$$f^{\prime} ( x )=2 ( x^{2}+a^{2} )$$
C.$$f^{\prime} ( x )=3 ( x^{2}-a^{2} )$$
D.$$f^{\prime} ( x )=3 ( x^{2}+a^{2} )$$
5、['简单复合函数的导数'， '导数与单调性'， '导数与极值']正确率40.0%设函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=x l n x$$，则$${{f}{（}{x}{）}}$$的极小值点为（）
D
A.$${{x}{=}{e}}$$
B.$$x=l n 2$$
C.$${{x}{=}{{e}^{2}}}$$
D.$$x=\frac{1} {e}$$
6、['简单复合函数的导数'， '导数的四则运算法则']正确率60.0%下列求导计算正确的是（）
B
A.$$( \frac{l n x} {x} ) ~^{\prime}=\frac{l n x-1} {x^{2}}$$
B.$$( l o g_{2} x ) ~^{\prime}=\frac{1} {x l n 2}$$
C.$$( \， 2^{x} \， )^{\prime}=2^{x} \， \frac{1} {l n 2}$$
D.$$( \ x \operatorname{s i n} x ) \rq{\prime}=\operatorname{c o s} x$$
7、['简单复合函数的导数'， '导数的四则运算法则'， '基本初等函数的导数']正确率60.0%已知$$f ( x )=\operatorname{s i n} x$$，则$$f^{\prime} ( x )=\langle$$）
A
A.$${{c}{o}{s}{x}}$$
B.$${{−}{{c}{o}{s}}{x}}$$
C.$${{t}{a}{n}{x}}$$
D.$${{−}{{t}{a}{n}}{x}}$$
8、['简单复合函数的导数'， '导数的四则运算法则'， '基本初等函数的导数']正确率60.0%下列求导式子正确的是$${{(}{)}}$$
C
A.$$( \frac{1} {\operatorname{l n} x} )^{\prime}=x$$
B.$$( \operatorname{s i n} 2 x )^{\prime}=2 \mathrm{c o s}^{2} x-1$$
C.$$( x-\frac{1} {x} )^{\prime}=1+\frac{1} {x^{2}}$$
D.$$( e^{-x} )^{\prime}=e^{-x}$$
9、['简单复合函数的导数'， '导数与单调性'， '利用导数求参数的取值范围']正确率40.0%若函数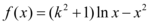
在区间$${{(}{1}}$$
A
A.$$[-1， 1 ]$$
B.$${{[}}$$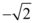
，
$${{]}}$$
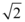C.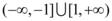
D.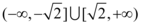
正确率60.0%设$$f ( x )=e^{-x}$$，则$$f^{\prime} ( x )=$$
A
A.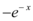
B.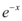
C.$${{−}{{e}^{x}}}$$
D.$${{e}^{x}}$$
1. 求导 $$f(x) = \ln(-x)$$，使用链式法则：$$f'(x) = \frac{1}{-x} \cdot (-1) = \frac{1}{x}$$。代入 $$x = -2024$$ 得 $$f'(-2024) = \frac{1}{-2024} = -\frac{1}{2024}$$。正确答案为 A。
2. 对 $$(3x-1)^5$$ 展开后求导：设 $$P(x) = a_0 + a_1x + a_2x^2 + \dots + a_5x^5$$，则 $$P'(x) = a_1 + 2a_2x + 3a_3x^2 + \dots + 5a_5x^4$$。在 $$x=1$$ 处求值：$$P'(1) = a_1 + 2a_2 + 3a_3 + 4a_4 + 5a_5$$。直接对 $$(3x-1)^5$$ 求导得 $$P'(x) = 5 \cdot 3(3x-1)^4 = 15(3x-1)^4$$，代入 $$x=1$$ 得 $$P'(1) = 15 \cdot (2)^4 = 240$$。正确答案为 D。
3. 对 $$f(x) = 2^x + \log_2 x$$ 求导：$$f'(x) = 2^x \ln 2 + \frac{1}{x \ln 2}$$。代入 $$x=1$$ 得 $$f'(1) = 2 \ln 2 + \frac{1}{\ln 2}$$。正确答案为 B。
4. 展开 $$f(x) = (x+2a)(x-a)^2$$ 并求导：先展开为 $$f(x) = (x+2a)(x^2 - 2a x + a^2) = x^3 - 2a x^2 + a^2 x + 2a x^2 - 4a^2 x + 2a^3 = x^3 - 3a^2 x + 2a^3$$。求导得 $$f'(x) = 3x^2 - 3a^2 = 3(x^2 - a^2)$$。正确答案为 C。
5. 对 $$f(x) = x \ln x$$ 求导：$$f'(x) = \ln x + 1$$。令导数为零，$$\ln x + 1 = 0$$ 解得 $$x = e^{-1} = \frac{1}{e}$$。验证二阶导数 $$f''(x) = \frac{1}{x} > 0$$，故 $$x = \frac{1}{e}$$ 是极小值点。正确答案为 D。
6. 逐项验证：
A. $$(\frac{\ln x}{x})' = \frac{1 \cdot x - \ln x \cdot 1}{x^2} = \frac{1 - \ln x}{x^2}$$，错误；
B. $$(\log_2 x)' = \frac{1}{x \ln 2}$$，正确；
C. $$(2^x)' = 2^x \ln 2$$，错误；
D. $$(x \sin x)' = \sin x + x \cos x$$，错误。
正确答案为 B。
7. 基本导数公式：$$(\sin x)' = \cos x$$。正确答案为 A。
8. 逐项验证：
A. $$(\frac{1}{\ln x})' = -\frac{1}{(\ln x)^2} \cdot \frac{1}{x}$$，错误；
B. $$(\sin 2x)' = 2 \cos 2x$$，错误；
C. $$(x - \frac{1}{x})' = 1 + \frac{1}{x^2}$$，正确；
D. $$(e^{-x})' = -e^{-x}$$，错误。
正确答案为 C。
9. 题目不完整，无法解析。
10. 对 $$f(x) = e^{-x}$$ 求导：$$f'(x) = -e^{-x}$$。正确答案为 B。