正确率40.0%若$$( 3 x-1 )^{5}=a_{0}+a_{1} x+a_{2} x^{2}+\dots$$$${{+}{{a}_{5}}{{x}^{5}}{,}}$$则$$a_{1}+2 a_{2}+3 a_{3}+4 a_{4}+5 a_{5}=$$()
D
A.$${{8}{0}}$$
B.$${{1}{2}{0}}$$
C.$${{1}{8}{0}}$$
D.$${{2}{4}{0}}$$
2、['正切曲线的对称中心', '正切(型)函数的周期性', '简单复合函数的导数', '函数的对称性', '函数零点的值或范围问题']正确率40.0%设函数$$f \left( x \right)=e^{x} \operatorname{s i n} \pi x$$,则方程$$x f \left( x \right)=f^{\prime} \left( x \right)$$在区间$$(-2 0 1 4, 2 0 1 6 )$$上的所有实根之和为$${{(}{)}}$$
B
A.$${{2}{0}{1}{5}}$$
B.$${{4}{0}{3}{0}}$$
C.$${{2}{0}{1}{6}}$$
D.$${{4}{0}{3}{2}}$$
3、['函数y=A sin(wx+φ)(A≠0,w不等于0)的图象及性质', '由图象(表)求三角函数的解析式', '简单复合函数的导数']正确率40.0%函数$$f \left( x \right)=A \operatorname{s i n} ( \omega x+\varphi) \left( A > 0, \omega> 0, | \varphi| < \frac{\pi} {2} \right)$$,已知其导函数$$f^{'} \left( x \right)$$的部分图象如图所示,则$${{f}{{(}{x}{)}}}$$的函数解析式为()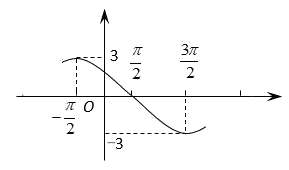
D
A.$$f \left( x \right)=3 \operatorname{s i n} \left( \frac{1} {2} x+\frac{\pi} {4} \right)$$
B.$$f \left( x \right)=6 \operatorname{s i n} \left( \frac{1} {2} x-\frac{\pi} {4} \right)$$
C.$$f \left( x \right)=3 \operatorname{s i n} \left( \frac{1} {2} x-\frac{\pi} {4} \right)$$
D.$$f \left( x \right)=6 \operatorname{s i n} \left( \frac{1} {2} x+\frac{\pi} {4} \right)$$
4、['函数奇偶性的应用', '简单复合函数的导数', '函数奇、偶性的图象特征', '函数图象的识别']正确率60.0%已知函数$$f \left( x \right)=x \cdot2^{\operatorname{c o s} x}$$,当$$x \in[-\pi, \pi]$$时,$${{y}{=}{f}{{(}{x}{)}}}$$的图象大致是()
B
A.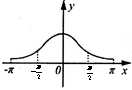
B.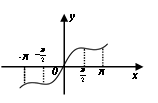
C.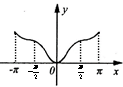
D.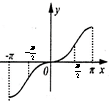
正确率60.0%如果$${{f}{(}{x}{)}}$$为偶函数,且$${{f}{(}{x}{)}}$$导数存在,则$${{f}{^{′}}{{(}{0}{)}}}$$的值为$${{(}{)}}$$
C
A.$${{2}}$$
B.$${{1}}$$
C.$${{0}}$$
D.$${{−}{1}}$$
6、['简单复合函数的导数', '利用导数求曲线的切线方程(斜率)', '导数的几何意义']正确率60.0%已知$${{e}}$$是自然对数的底数,函数$$f ( x )=\mathrm{e}^{x^{2}-3 x-4}$$的图象在点$$(-1, 1 )$$处的切线方程为()
D
A.$$x+y=0$$
B.$$x-y+2=0$$
C.$$5 x-y+6=0$$
D.$$5 x+y+4=0$$
7、['简单复合函数的导数']正确率60.0%函数$$y=\operatorname{c o s} \, \langle\, l n x \, \rangle$$的导数$${{y}^{′}{=}{(}}$$)
C
A.$$l n \textsubscript{( s i n x )}$$
B.$$\operatorname{s i n} \, ( l n x )$$
C.$$- \frac{1} {x} \mathrm{s i n} ~ ( \ l n x )$$
D.$$\frac{1} {x} \operatorname{s i n} ~ ( l n x )$$
8、['简单复合函数的导数']正确率60.0%函数$$y=f \left( e^{3 x} \right)$$,则导数$$y^{\prime}=( \textsubscript{\Lambda} )$$
D
A.$$3 f^{\prime} \left( e^{3 x} \right)$$
B.$$3 e^{3 x} \, f^{\prime} \, ( x )$$
C.$$e^{3 x} \, f^{\prime} \, \left( e^{3 x} \right)$$
D.$$3 e^{3 x} \, f^{\prime} \, \left( e^{3 x} \right)$$
9、['简单复合函数的导数', '导数的四则运算法则', '基本初等函数的导数']正确率60.0%函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=e^{-x}-2 f^{\prime} \left( \begin{matrix} {0} \\ {0} \\ \end{matrix} \right) \ \operatorname{l n} \left( \begin{matrix} {x+1} \\ \end{matrix} \right)$$,则$$f \left( \textbf{1} \right) ~+f^{\prime} \left( \textbf{1} \right) ~=$$()
C
A.$$\frac{-2 \operatorname{l n} 2+1} {3}$$
B.$$\frac{2} {\mathrm{e}}-\frac{2 \operatorname{l n} 2+1} {3}$$
C.$$\frac{2 \operatorname{l n} 2+1} {3}$$
D.$$\frac{2} {\mathrm{e}}-\frac{-2 \operatorname{l n} 2+1} {3}$$
10、['简单复合函数的导数']正确率60.0%$$y=\operatorname{s i n} ( 2 x+\frac{\pi} {3} )$$的导函数是()
B
A.$$y=\operatorname{c o s} ( 2 x+\frac{\pi} {3} )$$
B.$$y=2 \operatorname{c o s} ( 2 x+\frac{\pi} {3} )$$
C.$$y=-\operatorname{c o s} ( 2 x+\frac{\pi} {3} )$$
D.$$y=-2 \operatorname{c o s} ( 2 x+\frac{\pi} {3} )$$
1. 解析:
对 $$(3x-1)^5$$ 展开后,求 $$a_1 + 2a_2 + 3a_3 + 4a_4 + 5a_5$$。
首先,展开式的一般项为 $$a_k x^k$$,其中 $$a_k = C(5, k) \cdot 3^k \cdot (-1)^{5-k}$$。
我们需要计算的是 $$\sum_{k=1}^5 k a_k$$。
考虑对展开式求导:
$$f(x) = (3x-1)^5 = \sum_{k=0}^5 a_k x^k$$
求导得:
$$f'(x) = 15(3x-1)^4 = \sum_{k=1}^5 k a_k x^{k-1}$$
将 $$x=1$$ 代入:
$$f'(1) = 15(3 \cdot 1 - 1)^4 = 15 \cdot 16 = 240$$
即 $$\sum_{k=1}^5 k a_k = 240$$。
因此,答案为 $$\boxed{D}$$。
2. 解析:
解方程 $$x f(x) = f'(x)$$,其中 $$f(x) = e^x \sin \pi x$$。
首先计算导数:
$$f'(x) = e^x \sin \pi x + \pi e^x \cos \pi x = e^x (\sin \pi x + \pi \cos \pi x)$$
方程化为:
$$x e^x \sin \pi x = e^x (\sin \pi x + \pi \cos \pi x)$$
约去 $$e^x$$:
$$x \sin \pi x = \sin \pi x + \pi \cos \pi x$$
整理得:
$$(x-1) \sin \pi x - \pi \cos \pi x = 0$$
即:
$$\tan \pi x = \frac{\pi}{x-1}$$
在区间 $$(-2014, 2016)$$ 内,$$\tan \pi x$$ 的周期为 1,且在每个周期内有一个解。因此,解的个数为 $$2016 - (-2014) = 4030$$ 个。
由于 $$\tan \pi x$$ 和 $$\frac{\pi}{x-1}$$ 都是奇函数,解关于 $$x=0.5$$ 对称,因此所有解的和为 $$4030 \times 0.5 = 2015$$。
答案为 $$\boxed{A}$$。
3. 解析:
已知导函数 $$f'(x)$$ 的图像,求 $$f(x)$$ 的解析式。
导函数 $$f'(x) = A \omega \cos(\omega x + \phi)$$。
从图像中可以看出:
- 振幅为 $$A \omega = 3$$;
- 周期为 $$4\pi$$,因此 $$\omega = \frac{2\pi}{4\pi} = \frac{1}{2}$$;
- 当 $$x=0$$ 时,$$f'(0) = 3 \cos \phi = \frac{3\sqrt{2}}{2}$$,故 $$\cos \phi = \frac{\sqrt{2}}{2}$$,即 $$\phi = \frac{\pi}{4}$$。
因此,$$f(x) = A \sin\left(\frac{1}{2}x + \frac{\pi}{4}\right)$$,且 $$A \omega = 3$$,故 $$A = 6$$。
答案为 $$\boxed{D}$$。
4. 解析:
分析函数 $$f(x) = x \cdot 2^{\cos x}$$ 在 $$[-\pi, \pi]$$ 上的图像。
- 当 $$x=0$$ 时,$$f(0) = 0$$;
- 当 $$x \in (0, \pi]$$ 时,$$\cos x \in [-1, 1]$$,$$2^{\cos x} \in [\frac{1}{2}, 2]$$,因此 $$f(x)$$ 为正;
- 当 $$x \in [-\pi, 0)$$ 时,$$f(x)$$ 为负;
- 函数关于原点不对称,因为 $$f(-x) = -x \cdot 2^{\cos(-x)} = -x \cdot 2^{\cos x} \neq f(x)$$。
结合选项,最符合的是图像 $$\boxed{B}$$。
5. 解析:
已知 $$f(x)$$ 为偶函数且导数存在,求 $$f'(0)$$。
偶函数满足 $$f(-x) = f(x)$$,对其求导:
$$f'(-x) \cdot (-1) = f'(x)$$,即 $$f'(-x) = -f'(x)$$,故 $$f'(x)$$ 为奇函数。
奇函数在 $$x=0$$ 处有 $$f'(0) = -f'(0)$$,因此 $$f'(0) = 0$$。
答案为 $$\boxed{C}$$。
6. 解析:
求函数 $$f(x) = e^{x^2 - 3x - 4}$$ 在点 $$(-1, 1)$$ 处的切线方程。
首先验证 $$f(-1) = e^{1 + 3 - 4} = e^0 = 1$$,点在函数上。
计算导数:
$$f'(x) = e^{x^2 - 3x - 4} \cdot (2x - 3)$$
在 $$x=-1$$ 处:
$$f'(-1) = 1 \cdot (-2 - 3) = -5$$
切线方程为:
$$y - 1 = -5(x + 1)$$,即 $$5x + y + 4 = 0$$。
答案为 $$\boxed{D}$$。
7. 解析:
求 $$y = \cos(\ln x)$$ 的导数。
使用链式法则:
$$y' = -\sin(\ln x) \cdot \frac{1}{x} = -\frac{1}{x} \sin(\ln x)$$。
答案为 $$\boxed{C}$$。
8. 解析:
求 $$y = f(e^{3x})$$ 的导数。
使用链式法则:
$$y' = f'(e^{3x}) \cdot e^{3x} \cdot 3 = 3 e^{3x} f'(e^{3x})$$。
答案为 $$\boxed{D}$$。
9. 解析:
已知 $$f(x) = e^{-x} - 2 f'(0) \ln(x+1)$$,求 $$f(1) + f'(1)$$。
首先求 $$f'(x)$$:
$$f'(x) = -e^{-x} - 2 f'(0) \cdot \frac{1}{x+1}$$
在 $$x=0$$ 处:
$$f'(0) = -1 - 2 f'(0)$$,解得 $$f'(0) = -\frac{1}{3}$$。
因此:
$$f(x) = e^{-x} + \frac{2}{3} \ln(x+1)$$
$$f'(x) = -e^{-x} + \frac{2}{3(x+1)}$$
计算 $$f(1) + f'(1)$$:
$$f(1) = e^{-1} + \frac{2}{3} \ln 2$$
$$f'(1) = -e^{-1} + \frac{2}{6} = -e^{-1} + \frac{1}{3}$$
因此:
$$f(1) + f'(1) = \frac{2}{3} \ln 2 + \frac{1}{3} = \frac{2 \ln 2 + 1}{3}$$
答案为 $$\boxed{C}$$。
10. 解析:
求 $$y = \sin\left(2x + \frac{\pi}{3}\right)$$ 的导数。
使用链式法则:
$$y' = \cos\left(2x + \frac{\pi}{3}\right) \cdot 2 = 2 \cos\left(2x + \frac{\pi}{3}\right)$$。
答案为 $$\boxed{B}$$。
.jpg)