正确率60.0%已知函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=\left\{\begin{matrix} {\cos x-x, \ x \leqslant0} \\ {\frac{1-x} {x+1}, \ x > 0} \\ \end{matrix} \right.$$,则下列结论正确的是()
C
A.$${{f}{(}{x}{)}}$$有极值
B.$$y=f ~ ( x ) ~+1$$有零点
C.$${{f}{(}{x}{)}}$$在定义域上是减函数
D.$$f \left( \begin{matrix} {0} \\ \end{matrix} \right) \ =0$$
2、['利用导数讨论函数单调性', '导数中的函数构造问题', '利用函数单调性比较大小']正确率40.0%$${{f}{(}{x}{)}}$$对任意$${{x}{∈}{R}}$$都有$$f^{\prime} ( x ) > f ( x )$$成立,则$${{(}{)}}$$
A
A.$$3 f \, ( \operatorname{l n} \! 5 ) > 5 \, f \, ( \operatorname{l n} \! 3 )$$
B.$$3 f \, ( \operatorname{l n} \! 5 )=5 \, f \, ( \operatorname{l n} \! 3 )$$
C.$$3 f \, ( \operatorname{l n} \! 5 ) < 5 \, f \, ( \operatorname{l n} \! 3 )$$
D.$${{3}{f}{{(}{{l}{n}}{5}{)}}}$$与$${{5}{f}{{(}{{l}{n}}{3}{)}}}$$的大小不确定
3、['函数图象的识别', '利用导数讨论函数单调性']正确率60.0%如图,点$${{P}}$$是半径为$${{1}}$$的半圆弧$$\overrightarrow{A B}$$上一点,若$$\overrightarrow{A P}$$长度为$${{x}}$$,则直线$${{A}{P}}$$与半圆弧$$\overrightarrow{A B}$$所围成的图形的面积$${{S}}$$关于$${{x}}$$的函数图象为$${{(}{)}}$$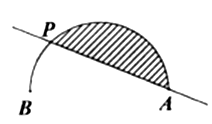
A
A.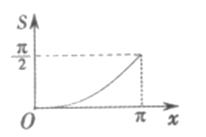
B.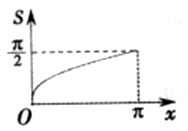
C.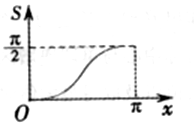
D.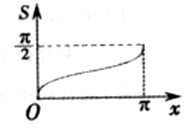
正确率40.0%已知定义域为$${{R}}$$奇函数$${{f}{(}{x}{)}}$$,其导函数为$$f^{\prime} ( x )$$,对任意正实数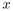 满足$$x f^{\prime} ( x ) >-2 f ( x )$$
满足$$x f^{\prime} ( x ) >-2 f ( x )$$
B
A.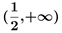
B.
C.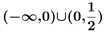
D.
正确率40.0%若函数$$f \left( x \right)=\frac{3} {2} x^{2}-1 2 x+9 \operatorname{l n} x+b$$恰有两个不同的零点,则实数$${{b}}$$可能的值为$${{(}{)}}$$
D
A.$$\frac{2 1} {2}$$
B.$$\frac{4 5} {2}$$
C.$${\frac{4 5} {2}}-9 l n 3$$
D.$$\frac{2 1} {2}$$或$${\frac{4 5} {2}}-9 l n 3$$
6、['导数与最值', '利用导数讨论函数单调性', '根据函数零点个数求参数范围']正确率40.0%已知$${{a}{∈}{R}}$$,函数$$f \left( x \right)=\frac1 2 \operatorname{l n} x+3 a$$和$$g \left( x \right)=\sqrt{x}+2 a^{2}$$的图象有交点,则$${{a}}$$的取值范围是
A
A.$$\left[ \frac{1} {2}, 1 \right]$$
B.$$[ 1,+\infty)$$
C.$$[ \frac{1} {2},+\infty)$$
D.$$[ 1, 2 ]$$
7、['函数图象的识别', '利用导数讨论函数单调性']正确率60.0%函数$$y=-\frac{\operatorname{c o s} x} {x}$$的图象可能是()
A
A.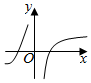
B.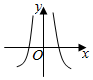
C.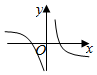
D.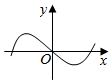
正确率60.0%已知函数$$f \left( x \right)=x^{3}-3 x+m$$,在区间$$[ 0, 2 ]$$上任取三个数$$a, ~ b, ~ c$$,均存在以$$f \left( a \right), \, \, f \left( b \right), \, \, f \left( c \right)$$为边长的三角形,则$${{m}}$$的取值范围是()
B
A.$$( 8,+\infty)$$
B.$$( 6,+\infty)$$
C.$$( 4,+\infty)$$
D.$$( 2,+\infty)$$
9、['利用导数讨论函数单调性']正确率40.0%若$${{f}{(}{x}{)}}$$是定义在$${{R}}$$上的可导函数,且![]() 的图象如图所示,则$$y=f ( x )$$
的图象如图所示,则$$y=f ( x )$$
D
A.$$(-\infty, 0 )$$
B.$$( 2,+\infty)$$
C.$$( 0, 1 )$$
D.$$( 0, 2 )$$
10、['利用导数讨论函数单调性', '导数中不等式恒成立与存在性问题']正确率40.0%已知函数$$f \left( x \right)=\frac{1} {2} m x \left( x-2 \right)+x \operatorname{l n} x-x$$,若对任意的$$x_{1}, ~ x_{2} \in\left[ \frac{1} {e}, 2 \right]$$,都有$$\left\vert f \left( x_{1} \right)-f \left( x_{2} \right) \right\vert\leqslant\frac{4} {\mathrm{e}}+1$$,则正实数$${{m}}$$的取值范围是()
A
A.$$( 0, \frac{8} {\mathrm{e}}+4 \operatorname{l n} \frac{\mathrm{e}} {2} \biggr]$$
B.$$\left[ \frac{8} {\mathrm{e}}+4 \operatorname{l n} \frac{\mathrm{e}} {2},+\infty\right)$$
C.$$\left( 0, {\frac{1 2 \mathrm{e}} {\left( \mathrm{e}-1 \right)^{2}}} \right]$$
D.$$\left[ \frac{1 2 \mathrm{e}} {\left( \mathrm{e}-1 \right)^{2}},+\infty) \right.$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)