正确率60.0%现有一个橡皮泥制作的底面半径为$${{4}{,}}$$高为$${{3}}$$的圆锥.若将它重新制作成一个底面半径为$${{r}{,}}$$高为$${{h}}$$的圆柱(橡皮泥没有浪费),则该圆柱表面积的最小值为()
B
A.$${{2}{0}{π}}$$
B.$${{2}{4}{π}}$$
C.$${{2}{8}{π}}$$
D.$${{3}{2}{π}}$$
2、['利用导数解决实际应用问题', '棱柱、棱锥、棱台的体积']正确率60.0%如图,将边长为$${{1}}$$的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(容器厚度忽略不计).当这个正六棱柱的容积最大时,它的底面边长为()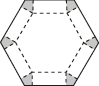
B
A.$$\frac{3} {4}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\frac{1} {3}$$
D.$$\frac{1} {2}$$
3、['一元二次不等式恒成立问题', '利用导数解决实际应用问题']正确率80.0%对于任意实数$${{x}}$$,不等式$$( a-1 ) x^{2}-2 ( a-1 ) x-4 < 0$$恒成立,则实数$${{a}}$$的取值范围是$${{(}{)}}$$
A.$$(-\infty, 3 )$$
B.$$(-\infty, 3 ]$$
C.$$(-3, 1 )$$
D.$$(-3, 1 ]$$
4、['利用导数解决实际应用问题', '归纳推理']正确率60.0%二维空间中,圆的一维测度(周长$$) \, \, l=2 \pi r$$,二维测度(面积$$\mu\ S=\pi r^{2}$$,三维空间中,球的二维测度(表面积$$\mu\ S=4 \pi r^{2}$$,三维测度(体积$$V={\frac{4} {3}} \pi r^{3}$$,应用合情推理,若四维空间中,$${{“}}$$超球$${{”}}$$的三维测度$$V=8 \pi r^{3}$$,则其四维测度$${{W}{=}}$$()
A
A.$${{2}{π}{{r}^{4}}}$$
B.$${{3}{π}{{r}^{4}}}$$
C.$${{4}{π}{{r}^{4}}}$$
D.$${{6}{π}{{r}^{4}}}$$
正确率40.0%某公司生产一种产品,固定成本为$${{2}{0}{{0}{0}{0}}}$$元,每生产$${{1}}$$件产品成本增加$${{1}{0}{0}}$$元,若总收入$${{R}{(}{x}{)}}$$(单位:元)与年产量$${{x}}$$(单位:件)的关系式是$$R ( x )=\left\{\begin{aligned} {} & {{}-\frac{x^{3}} {9 0 0}+4 0 0 x, \ 0 \leqslant x \leqslant3 9 0.} \\ {} & {{} 9 0 \ 0 9 0, \ x > 3 9 0.} \\ \end{aligned} \right.$$则当总利润最大时,每年生产产品的件数是()
D
A.$${{1}{5}{0}}$$
B.$${{2}{0}{0}}$$
C.$${{2}{5}{0}}$$
D.$${{3}{0}{0}}$$
6、['利用导数解决实际应用问题', '瞬时变化率']正确率80.0%如果说某物体作直线运动的时间与距离满足$$s ( t )=2 ( 1-t )^{2}$$,则其在$${{t}{=}{{1}{.}{2}}}$$时的瞬时速度为()
D
A.$${{4}}$$
B.$${{−}{4}}$$
C.$${{4}{.}{8}}$$
D.$${{0}{.}{8}}$$
7、['导数与最值', '利用导数解决实际应用问题']正确率40.0%某淘宝店每季度最大销售量$${{4}{0}{0}}$$件,每销售一件商品成本增加$${{1}{0}{0}}$$元,如果收入函数是$$R \left( q \right) \!=\!-\frac{1} {2} q^{2} \!+\! 4 0 0 q ( q \allowbreak\! \coloneqq\allowbreak\! \emptyset\n\# \allowbreak\! \models\allowbreak\! )$$,则当总利润最大时,商品销售量为$${{(}{)}}$$
B
A.$${{2}{0}{0}}$$
B.$${{3}{0}{0}}$$
C.$${{3}{5}{0}}$$
D.$${{4}{0}{0}}$$
8、['导数与最值', '利用导数解决实际应用问题']正确率40.0%一个箱子的容积与底面边长$${{x}}$$的关系为$$V \left( x \right)=x^{2} \left( \frac{6 0-x} {2} \right) ( 0 < x < 6 0 )$$,则当箱子的容积最大时,$${{x}}$$的值为$${{(}{)}}$$
B
A.$${{3}{0}}$$
B.$${{4}{0}}$$
C.$${{5}{0}}$$
D.$${{6}{0}}$$
9、['导数与最值', '利用导数解决实际应用问题']正确率40.0%某产品的销售收入$${{y}_{1}{(}}$$万元$${{)}}$$是产量$${{x}{(}}$$千台$${{)}}$$的函数,且函数解析式为$$y_{1}=1 7 x^{2} ( x > 0 )$$,生产成本$${{y}_{2}{(}}$$万元$${{)}}$$是产量$${{x}{(}}$$千台$${{)}}$$的函数,且函数解析式为$$y_{2}=2 x^{3}-x^{2} ( x > 0 )$$,要使利润最大,则该产品应生产$${{(}{)}}$$
A
A.$${{6}}$$千台
B.$${{7}}$$千台
C.$${{8}}$$千台
D.$${{9}}$$千台
10、['导数与单调性', '利用导数解决实际应用问题']正确率40.0%若关于$${{x}}$$的不等式$$a x-2 a > 2 x-\operatorname{l n} x-4$$有且只有两个整数解,则实数$${{a}}$$的取值范围是$${{(}{)}}$$
C
A.$$( 2-\operatorname{l n} 3, 2-\operatorname{l n} 2 ]$$
B.$$(-\infty, 2-\operatorname{l n} 2 )$$
C.$$(-\infty, 2-\operatorname{l n} 3 ]$$
D.$$(-\infty, 2-\operatorname{l n} 3 )$$
1、圆锥的体积为 $$V = \frac{1}{3} \pi r^2 h = \frac{1}{3} \pi \times 4^2 \times 3 = 16\pi$$。重新制作成圆柱后,体积不变,即 $$\pi r^2 h = 16\pi$$,得 $$h = \frac{16}{r^2}$$。圆柱的表面积为 $$S = 2\pi r^2 + 2\pi r h = 2\pi r^2 + \frac{32\pi}{r}$$。对 $$S$$ 关于 $$r$$ 求导并令导数为零,得 $$4\pi r - \frac{32\pi}{r^2} = 0$$,解得 $$r = 2$$。代入得 $$h = 4$$,此时表面积 $$S = 2\pi \times 2^2 + 2\pi \times 2 \times 4 = 24\pi$$。答案为 $$\boxed{B}$$。
3、当 $$a = 1$$ 时,不等式化为 $$-4 < 0$$,恒成立。当 $$a \neq 1$$ 时,需满足 $$a - 1 < 0$$ 且判别式 $$\Delta = 4(a - 1)^2 + 16(a - 1) < 0$$,解得 $$-3 < a < 1$$。综上,$$a \in (-3, 1]$$。答案为 $$\boxed{D}$$。
5、总利润为 $$P(x) = R(x) - (20000 + 100x)$$。当 $$0 \leq x \leq 390$$ 时,$$P(x) = -\frac{x^3}{900} + 300x - 20000$$,求导得极值点 $$x = 300$$。比较 $$x = 300$$ 和 $$x = 390$$ 的利润,$$x = 300$$ 时利润最大。答案为 $$\boxed{D}$$。
7、总利润为 $$P(q) = R(q) - 100q = -\frac{1}{2} q^2 + 300q$$。求导得极值点 $$q = 300$$。答案为 $$\boxed{B}$$。
9、利润为 $$P(x) = y_1 - y_2 = 17x^2 - (2x^3 - x^2) = -2x^3 + 18x^2$$。求导得极值点 $$x = 6$$。答案为 $$\boxed{A}$$。
.jpg)