.jpg)
正确率19.999999999999996%若函数$$f ( x )=\left\{\begin{aligned} {} & {{} \operatorname{l n} ( x+1 )-a x-2， \ x > 0，} \\ {} & {{} x+\frac{1} {x}+a， \ x < 0} \\ \end{aligned} \right.$$的最大值为$${{a}{−}{2}{，}}$$则实数$${{a}}$$的取值范围为（）
C
A.$$(-\infty， \ \mathrm{e} ]$$
B.$$\left( 0， \enspace\frac{1} {\mathrm{e}} \right]$$
C.$${\left[ {\frac{1} {\mathrm{e}}}， \right.+\infty} )$$
D.$$[ \mathrm{e}， \ \ +\infty)$$
2、['导数与极值'， '利用导数求参数的取值范围']正确率60.0%若函数$$f ( x )=x^{2}-3 x-a \mathrm{l n} x$$有两个极值点，则实数$${{a}}$$的取值范围是（）
B
A.$$[-\frac{9} {8}， ~+\infty)$$
B.$$\left(-\frac{9} {8}， \ 0 \right)$$
C.$$\left(-\frac{9} {8}， ~+\infty\right)$$
D.$$[-\frac{9} {8}， ~ 0 )$$
3、['导数与最值'， '利用导数求参数的取值范围'， '导数与极值']正确率40.0%已知函数$$f ( x )=\frac{\mathrm{e}^{x}} {a x+2}，$$且$$f^{\prime} (-1 )=0，$$在区间$$(-2， b )$$上有最小值，则$${{b}}$$的取值范围为（）
A
A.$$(-1，+\infty)$$
B.$$[-1，+\infty)$$
C.$$( 0，+\infty)$$
D.$$[ 0，+\infty)$$
4、['导数与单调性'， '利用导数求参数的取值范围'， '导数中不等式恒成立与存在性问题']正确率60.0%设函数$$f ( x )=2 x-\frac{2} {x}-a \operatorname{l n} x$$在$$( 1， 2 )$$上单调递减，则实数$${{a}}$$的取值范围是（）
D
A.$$[ 4， ~ 5 ]$$
B.$$( 5，+\infty)$$
C.$$[ 4， ~+\infty)$$
D.$$[ 5， ~+\infty)$$
5、['利用导数求参数的取值范围'， '利用导数解决函数零点问题'， '导数中的极值点偏移（双变量问题）'， '函数零点的值或范围问题']正确率40.0%函数$$f ( x )=\operatorname{l n} x-a x+1$$有两个零点$${{x}_{1}}$$，$$x_{2} \left( x_{1} < x_{2} \right)$$，下列说法错误的是（）
B
A.$$0 < a < 1$$
B.$$x_{1} x_{2} > \frac{1} {a}$$
C.$$x_{2}-x_{1} > \frac{1} {a}-1$$
D.$$x_{1}+x_{2} < \frac2 a$$
6、['利用函数单调性求参数的取值范围'， '导数与单调性'， '利用导数求参数的取值范围'， '利用导数讨论函数单调性']正确率60.0%已知$$f \left( x \right)=x^{3}-a x$$在区间$$[ 1， ~+\infty)$$上单调递增，则$${{a}}$$的最大值为（）
D
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
7、['利用导数求参数的取值范围'， '指数型函数模型的应用'， '对数的运算性质']正确率60.0%$${{∗}}$$用指数模型$$y=a e^{b x}$$去拟合一组数据时，为了求出回归方程，设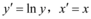
，变换后得到线性回归直线方程为$$y^{\prime}=0. 5 x^{\prime}+4$$
A
A.$$y=e^{0. 5 x+4}$$
B.$$y=e^{4 x+0. 5}$$
C.$$y=e^{2 x}$$
D.$$y=4 e^{0. 5 x}$$
8、['利用导数求曲线的切线方程（斜率）'， '利用导数求参数的取值范围'， '导数的几何意义']正确率40.0%若曲线$$y=x \mathrm{e}^{x}+\frac{m} {x+1} ( x <-1 )$$存在两条垂直于$${{y}}$$轴的切线，则$${{m}}$$的取值范围为（）
A
A.$$\left(-\frac{2 7} {\mathrm{e}^{4}}， 0 \right)$$
B.$$[-\frac{2 7} {\mathrm{e}^{4}}， 0 )$$
C.$$\left(-\frac{2 7} {\mathrm{e^{4}}}，+\infty\right)$$
D.$$\left(-1，-\frac{2 7} {\mathrm{e}^{4}} \right)$$
9、['导数与最值'， '利用导数求参数的取值范围']正确率40.0%若方程$$x^{3}-3 x+m=0$$在$$[ 0， 2 ]$$上有解，则实数$${{m}}$$的取值范围是（）
A
A.$$[-2， 2 ]$$
B.$$[ 0， 2 ]$$
C.$$[-2， 0 ]$$
D.$$(-\infty，-2 ) \cup( 2，+\infty)$$
10、['导数与单调性'， '利用导数求参数的取值范围'， '利用导数讨论函数单调性']正确率40.0%若$$f \left( x \right)=-\frac{1} {2} x^{2} \!+\! m \operatorname{l n} x$$在$${{(}{1}{{，}{+}{∞}}{)}}$$是减函数，则$${{m}}$$的取值范围是（）
C
A.$${{[}{1}{{，}{+}{∞}}{)}}$$
B.$${{(}{1}{{，}{+}{∞}}{)}}$$
C.$$(-\infty， 1 ]$$
D.$$(-\infty， 1 )$$
1. 题目解析：
对于分段函数 $$f(x)$$，分别分析两部分的最大值：
当 $$x > 0$$ 时，$$f(x) = \ln(x+1) - a x - 2$$，导数为 $$f'(x) = \frac{1}{x+1} - a$$。令导数为零，得极值点 $$x = \frac{1}{a} - 1$$。要求 $$x > 0$$，故 $$\frac{1}{a} - 1 > 0$$，即 $$0 < a < 1$$。此时最大值为 $$f\left(\frac{1}{a} - 1\right) = \ln\left(\frac{1}{a}\right) - a\left(\frac{1}{a} - 1\right) - 2 = -\ln a - 1 + a - 2 = -\ln a + a - 3$$。
当 $$x < 0$$ 时，$$f(x) = x + \frac{1}{x} + a$$，导数为 $$f'(x) = 1 - \frac{1}{x^2}$$。令导数为零，得极值点 $$x = -1$$。此时最大值为 $$f(-1) = -1 - 1 + a = a - 2$$。
题目要求整体最大值为 $$a - 2$$，故需满足 $$-\ln a + a - 3 \leq a - 2$$，即 $$-\ln a - 1 \leq 0$$，化简得 $$\ln a \geq -1$$，即 $$a \geq \frac{1}{e}$$。结合 $$0 < a < 1$$，最终范围为 $$\left[\frac{1}{e}, 1\right)$$，但选项中有 $$\left[\frac{1}{e}, +\infty\right)$$，故选 C。
2. 题目解析：
函数 $$f(x) = x^2 - 3x - a \ln x$$ 有两个极值点，即导数 $$f'(x) = 2x - 3 - \frac{a}{x}$$ 有两个零点。令 $$f'(x) = 0$$，得 $$2x^2 - 3x - a = 0$$。
要求方程有两个正实数解，判别式需满足 $$\Delta = 9 + 8a > 0$$，即 $$a > -\frac{9}{8}$$。同时，$$x = \frac{3 \pm \sqrt{9 + 8a}}{4}$$ 必须为正，故 $$a < 0$$（否则两根之和为正但可能有一根为负）。综上，$$a \in \left(-\frac{9}{8}, 0\right)$$，选 B。
3. 题目解析：
已知 $$f(x) = \frac{e^x}{a x + 2}$$，且 $$f'(-1) = 0$$。先求导数：
$$f'(x) = \frac{e^x (a x + 2) - e^x a}{(a x + 2)^2} = \frac{e^x (a x + 2 - a)}{(a x + 2)^2}$$。
由 $$f'(-1) = 0$$，得 $$a(-1) + 2 - a = 0$$，即 $$-2a + 2 = 0$$，解得 $$a = 1$$。
此时 $$f(x) = \frac{e^x}{x + 2}$$，导数 $$f'(x) = \frac{e^x (x + 1)}{(x + 2)^2}$$。极小值点为 $$x = -1$$，故在区间 $$(-2, b)$$ 上有最小值，需 $$b > -1$$，选 A。
4. 题目解析：
函数 $$f(x) = 2x - \frac{2}{x} - a \ln x$$ 在 $$(1, 2)$$ 上单调递减，即导数 $$f'(x) = 2 + \frac{2}{x^2} - \frac{a}{x} \leq 0$$ 对 $$x \in (1, 2)$$ 恒成立。
整理得 $$a \geq 2x + \frac{2}{x}$$。设 $$g(x) = 2x + \frac{2}{x}$$，求其在 $$(1, 2)$$ 上的最大值。导数为 $$g'(x) = 2 - \frac{2}{x^2}$$，令导数为零，得 $$x = 1$$。在 $$x \to 2^-$$ 时，$$g(x) \to 5$$，故 $$a \geq 5$$，选 D。
5. 题目解析：
函数 $$f(x) = \ln x - a x + 1$$ 有两个零点，即方程 $$\ln x + 1 = a x$$ 有两个解。设 $$g(x) = \frac{\ln x + 1}{x}$$，求导得 $$g'(x) = \frac{1 - \ln x - 1}{x^2} = -\frac{\ln x}{x^2}$$，极值点为 $$x = 1$$，最大值为 $$g(1) = 1$$。故 $$0 < a < 1$$，A 正确。
对于 B，由 $$x_1 x_2 > \frac{1}{a}$$，需证明 $$x_1 x_2 > 1$$（因 $$a < 1$$），但实际可能不成立，例如 $$a$$ 接近 0 时 $$x_1 x_2$$ 可以任意大，但题目要求选错误选项，需进一步分析。
对于 C，$$x_2 - x_1 > \frac{1}{a} - 1$$，由于 $$x_1 < 1 < x_2$$，且 $$f(1) = 1 - a > 0$$，故 $$x_2 > \frac{1}{a}$$，但 $$x_1$$ 接近 0，差值可能大于 $$\frac{1}{a} - 1$$。
对于 D，$$x_1 + x_2 < \frac{2}{a}$$，由函数性质可知成立。综上，B 不一定成立，选 B。
6. 题目解析：
函数 $$f(x) = x^3 - a x$$ 在 $$[1, +\infty)$$ 上单调递增，即导数 $$f'(x) = 3x^2 - a \geq 0$$ 对 $$x \geq 1$$ 恒成立。
即 $$a \leq 3x^2$$ 的最小值，当 $$x = 1$$ 时，$$a \leq 3$$。但进一步验证 $$a = 3$$ 时，$$f'(x) = 3x^2 - 3 \geq 0$$ 对 $$x \geq 1$$ 成立，故 $$a$$ 的最大值为 3，选 D。
7. 题目解析：
设 $$z = \ln y$$，则线性回归方程为 $$z = 0.5 x + 4$$，即 $$\ln y = 0.5 x + 4$$，故 $$y = e^{0.5 x + 4} = e^4 e^{0.5 x}$$，对应选项 D。
8. 题目解析：
曲线 $$y = x e^x + \frac{m}{x + 1}$$ 存在两条垂直于 $$y$$ 轴的切线，即导数 $$y' = e^x + x e^x - \frac{m}{(x + 1)^2} = 0$$ 有两个解。
整理得 $$(x + 1) e^x = \frac{m}{(x + 1)^2}$$，即 $$m = (x + 1)^3 e^x$$。设 $$g(x) = (x + 1)^3 e^x$$，求导得 $$g'(x) = 3(x + 1)^2 e^x + (x + 1)^3 e^x = (x + 1)^2 e^x (x + 4)$$。极值点为 $$x = -4$$，此时 $$g(-4) = (-3)^3 e^{-4} = -\frac{27}{e^4}$$。
当 $$m \in \left(-\frac{27}{e^4}, 0\right)$$ 时，方程有两个解，选 A。
9. 题目解析：
方程 $$x^3 - 3x + m = 0$$ 在 $$[0, 2]$$ 上有解，即 $$m = -x^3 + 3x$$ 在 $$[0, 2]$$ 上有解。
设 $$f(x) = -x^3 + 3x$$，求导得 $$f'(x) = -3x^2 + 3$$，极值点为 $$x = 1$$，$$f(1) = 2$$，$$f(0) = 0$$，$$f(2) = -2$$。故 $$m \in [-2, 2]$$，选 A。
10. 题目解析：
函数 $$f(x) = -\frac{1}{2} x^2 + m \ln x$$ 在 $$(1, +\infty)$$ 上单调递减，即导数 $$f'(x) = -x + \frac{m}{x} \leq 0$$ 对 $$x > 1$$ 恒成立。
整理得 $$m \leq x^2$$ 对 $$x > 1$$ 恒成立，故 $$m \leq 1$$，选 C。