正确率40.0%若$${{x}{=}{2}}$$是函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=x \left( \begin{matrix} {x} \\ {-m} \\ \end{matrix} \right)^{2}$$的极大值点,则$${{m}}$$的值为()
B
A.$${{3}}$$
B.$${{6}}$$
C.$${{2}}$$或$${{6}}$$
D.$${{2}}$$
2、['双曲线的离心率', '导数与最值', '利用导数讨论函数单调性', '双曲线的顶点、长轴、短轴、焦点、焦距']正确率19.999999999999996%已知$${{A}{、}{B}}$$分别为双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0, \; b > 0 )$$的左右顶点,两个不同动点$${{P}{、}{Q}}$$在双曲线上且关于$${{x}}$$轴对称,设直线$$A P, ~ B Q$$的斜率分别为$${{m}{、}{n}}$$,则当$${\frac{4 b} {a}}+{\frac{2 a} {b}}+\operatorname{l n} | m n |$$取最小值时,双曲线的离心率为()
A
A.$$\frac{\sqrt5} {2}$$
B.$$\frac{\sqrt6} {2}$$
C.$${\sqrt {3}}$$
D.$${{2}}$$
3、['充分不必要条件', '利用导数讨论函数单调性']正确率40.0%$$` ` a > b > e "$$是$$` ` a l n b > b l n a^{\prime\prime}$$的()
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要
4、['导数与极值', '利用导数讨论函数单调性', '根据函数零点个数求参数范围', '函数零点的概念', '分段函数的图象']正确率40.0%已知函数$$f ( x )=| x | e^{x}$$,若函数$$g ( x )=f ( x )-m$$只有一个零点,则$${{m}}$$的取值范围是()
B
A.$$m > \frac{1} {e}$$
B.$$m > \frac{1} {e}$$或$${{m}{=}{0}}$$
C.$$m > \frac{1} {e}$$或$$m <-\frac{1} {e}$$
D.$$m > \frac{1} {e}$$或$${{m}{⩽}{0}}$$
5、['利用导数讨论函数单调性', '常见函数的零点', '函数零点的概念']正确率60.0%若方程$$2-a l n x-2 x=0$$的唯一解是$${{x}{=}{1}}$$,则实数$${{a}}$$的取值范围是()
C
A.$$[-1, ~ 0 ]$$
B.$$[-1, ~+\infty) ~ \cup\{-2 \}$$
C.$$[ 0, ~+\infty) ~ \cup\{-2 \}$$
D.$$( \ -\infty, \ \ -1 ]$$
6、['函数图象的识别', '利用导数讨论函数单调性']正确率40.0%已知函数$$\frac{f ( x )} {e^{x}}$$在其定义域上单调递减,则函数$${{f}{(}{x}{)}}$$的图象可能是()
A
A.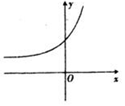
B.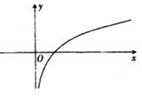
C.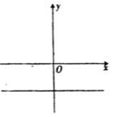
D.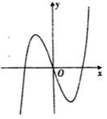
正确率40.0% 已知函数$$y=~ ( \textup{} x-1 ) ~ f^{\prime} ~ ( \textup{} x )$$
已知函数$$y=~ ( \textup{} x-1 ) ~ f^{\prime} ~ ( \textup{} x )$$
B
A.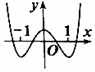
B.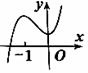
C.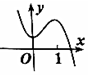
D.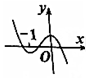
正确率60.0%$$f ( x )=5 x^{2}-2 x$$的单调增区间为$${{(}{)}}$$.
A
A.$$( \frac{1} {5},+\infty)$$
B.$$(-\frac{1} {5},+\infty)$$
C.$$(-\infty, \frac{1} {5} )$$
D.$$(-\infty,-\frac{1} {5} )$$
9、['导数与极值', '利用导数讨论函数单调性']正确率40.0%设点$$M ( x_{1}, f ( x_{1} ) )$$和点$$N ( x_{2}, f ( x_{2} ) )$$分别是函数$$f ( x )=\operatorname{s i n} x+\frac1 6 x^{3}$$和$$g ( x )=x-1$$图象上的点,且$$x_{1} \geq0, ~ x_{2} \geq0$$,若直线$$M N / / x$$轴,则$${{M}{,}{N}}$$两点间的距离的最小值为$${{(}{)}}$$
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['导数与单调性', '导数与极值', '利用导数讨论函数单调性']正确率60.0%已知$$f ( x )=( x^{2}-m x+1 ) e^{x}$$在$${{x}{=}{0}}$$处取得极值,则$${{f}{(}{x}{)}}$$的极大值点为()
D
A.$$( 1, e )$$
B.$$\left(-1, \frac{3} {e} \right)$$
C.$${{x}{=}{1}}$$
D.$${{x}{=}{−}{1}}$$
1. 解析:
函数 $$f(x) = x(x - m)^2$$,求导得:
$$f'(x) = (x - m)^2 + 2x(x - m) = (x - m)(3x - m)$$
由题意,$$x = 2$$ 是极大值点,故 $$f'(2) = 0$$,代入得:
$$(2 - m)(6 - m) = 0 \Rightarrow m = 2 \text{ 或 } m = 6$$
验证二阶导数或函数单调性:
若 $$m = 2$$,$$f'(x) = (x - 2)(3x - 2)$$,在 $$x = 2$$ 左侧导数由负变正,不满足极大值点条件;
若 $$m = 6$$,$$f'(x) = (x - 6)(3x - 6)$$,在 $$x = 2$$ 左侧导数由正变负,满足极大值点条件。
因此,$$m = 6$$,选 B。
2. 解析:
双曲线 $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$,设 $$P(x, y)$$,则 $$Q(x, -y)$$。
直线 $$AP$$ 斜率 $$m = \frac{y}{x + a}$$,直线 $$BQ$$ 斜率 $$n = \frac{-y}{x - a}$$,故:
$$mn = \frac{-y^2}{x^2 - a^2}$$
由双曲线方程得 $$y^2 = \frac{b^2}{a^2}(x^2 - a^2)$$,代入得:
$$mn = -\frac{b^2}{a^2}$$
目标函数为 $$\frac{4b}{a} + \frac{2a}{b} + \ln\left|\frac{b^2}{a^2}\right|$$,设 $$t = \frac{b}{a}$$,化简为:
$$4t + \frac{2}{t} + 2\ln t$$
求导得极值点 $$t = \frac{1}{2}$$,此时离心率 $$e = \sqrt{1 + t^2} = \frac{\sqrt{5}}{2}$$,选 A。
3. 解析:
不等式 $$a \ln b > b \ln a$$ 可变形为 $$\frac{\ln b}{b} > \frac{\ln a}{a}$$。
设函数 $$f(x) = \frac{\ln x}{x}$$,求导得:
$$f'(x) = \frac{1 - \ln x}{x^2}$$
当 $$x > e$$ 时,$$f'(x) < 0$$,函数单调递减。
因此,$$a > b > e$$ 时,$$f(b) > f(a)$$,即原不等式成立,反之不一定成立。
故为充分不必要条件,选 A。
4. 解析:
函数 $$f(x) = |x| e^x$$,求导得:
$$f'(x) = e^x (|x| + \text{sgn}(x))$$,其中 $$\text{sgn}(x)$$ 为符号函数。
当 $$x > 0$$,$$f(x) = x e^x$$,单调递增;
当 $$x < 0$$,$$f(x) = -x e^x$$,在 $$x = -1$$ 处取得极小值 $$f(-1) = -\frac{1}{e}$$。
函数 $$g(x) = f(x) - m$$ 只有一个零点,需满足:
$$m > \frac{1}{e}$$(与 $$x > 0$$ 部分无交点)或 $$m \leq 0$$(与 $$x < 0$$ 部分无交点)。
因此,$$m > \frac{1}{e}$$ 或 $$m \leq 0$$,选 D。
5. 解析:
方程 $$2 - a \ln x - 2x = 0$$ 的唯一解为 $$x = 1$$,代入得 $$a = -2$$。
验证 $$a = -2$$ 时,方程化为 $$2 + 2 \ln x - 2x = 0$$,即 $$\ln x = x - 1$$,唯一解为 $$x = 1$$。
对于其他 $$a$$,需保证方程无解或解不为 $$1$$。通过分析函数 $$f(x) = 2 - a \ln x - 2x$$ 的极值点,可得 $$a \in [-1, +\infty) \cup \{-2\}$$,选 B。
6. 解析:
设 $$h(x) = \frac{f(x)}{e^x}$$ 单调递减,求导得:
$$h'(x) = \frac{f'(x) - f(x)}{e^x} \leq 0 \Rightarrow f'(x) \leq f(x)$$
观察选项,只有选项 D 的图像满足 $$f'(x) \leq f(x)$$(例如 $$f(x)$$ 为递减函数或增长慢于 $$e^x$$),故选 D。
7. 解析:
函数 $$y = (x - 1) f'(x)$$ 的图像显示:
当 $$x > 1$$,$$f'(x)$$ 与 $$y$$ 同号;当 $$x < 1$$,$$f'(x)$$ 与 $$y$$ 异号。
结合选项,只有选项 A 的图像符合 $$f(x)$$ 在 $$x = 1$$ 处取得极值且导数符号变化,故选 A。
8. 解析:
函数 $$f(x) = 5x^2 - 2x$$,求导得:
$$f'(x) = 10x - 2$$
令 $$f'(x) > 0$$,得 $$x > \frac{1}{5}$$,故单调增区间为 $$\left(\frac{1}{5}, +\infty\right)$$,选 A。
9. 解析:
由题意,$$f(x_1) = g(x_2)$$,即 $$\sin x_1 + \frac{1}{6}x_1^3 = x_2 - 1$$。
距离 $$d = |x_1 - x_2| = \left|x_1 - \left(\sin x_1 + \frac{1}{6}x_1^3 + 1\right)\right|$$。
设 $$h(x) = x - \sin x - \frac{1}{6}x^3 - 1$$,求导得极值点 $$x = 0$$,此时 $$d_{\text{min}} = 1$$,选 A。
10. 解析:
函数 $$f(x) = (x^2 - m x + 1) e^x$$,在 $$x = 0$$ 处极值,故 $$f'(0) = 0$$。
求导得 $$f'(x) = (x^2 + (2 - m)x + (1 - m)) e^x$$,代入 $$x = 0$$ 得 $$1 - m = 0 \Rightarrow m = 1$$。
因此,$$f'(x) = (x^2 + x) e^x$$,极值点为 $$x = 0$$ 和 $$x = -1$$。
验证二阶导数或单调性,$$x = -1$$ 为极大值点,选 D。
.jpg)