正确率40.0%海轮每小时的燃料费与它的航行速度的立方成正比,已知某海轮的最大航行速度为$${{3}{0}}$$海里/时,当航行速度为$${{1}{0}}$$海里/时时,它的燃料费是每小时$${{2}{5}}$$元,其余费用(无论速度如何)是每小时$${{4}{0}{0}}$$元.如果甲乙两地相距$${{8}{0}{0}}$$海里,则要使该海轮从甲地航行到乙地的总费用最低,它的航行速度应为()
C
A.$${{3}{0}}$$海里/时
B.$${{2}{5}}$$海里/时
C.$${{2}{0}}$$海里/时
D.$${{1}{0}}$$海里/时
2、['利用导数解决实际应用问题']正确率40.0%已知等腰梯形的上底长为$${{7}{,}}$$腰长为$${{2}{,}}$$那么该等腰梯形的面积最大时,下底长为()
B
A.$$\frac{1 5} {2}$$
B.$${{8}}$$
C.$$\frac{1 7} {2}$$
D.$${{9}}$$
3、['导数与最值', '利用导数解决实际应用问题']正确率40.0%一个矩形的两个顶点在半径为$${{R}}$$的半圆的直径上,另外两个顶点在该半圆的弧上,当矩形的周长最大时,矩形的两边长分别为()
B
A.$$\frac{R} {2}$$和$${\frac{3} {2}} R$$
B.$$\frac{\sqrt{5}} {5} R$$和$$\frac{4 \sqrt{5}} {5} R$$
C.$${\frac{4} {5}} R$$和$${\frac{7} {5}} R$$
D.以上都不对
4、['导数与最值', '利用导数解决实际应用问题']正确率40.0%某品牌小汽车在匀速行驶中每小时的耗油量$${{y}{(}}$$升)关于行驶速度$${{x}{(}}$$千米$${{/}}$$时)的函数解析式为$$y=\frac1 {8 1 0 0 0} x^{3}-\frac1 {1 0} x+1 8 ( 0 < x \leqslant1 2 0 )$$.若要使该汽车行驶$${{2}{0}{0}}$$千米时的油耗最低,则汽车匀速行驶的速度应为()
C
A.$${{6}{0}}$$千米$${{/}}$$时
B.$${{8}{0}}$$千米$${{/}}$$时
C.$${{9}{0}}$$千米$${{/}}$$时
D.$${{1}{0}{0}}$$千米$${{/}}$$时
5、['圆柱的结构特征及其性质', '利用导数解决实际应用问题', '圆柱、圆锥、圆台的体积']正确率60.0%如果圆柱轴截面的周长为$${{1}}$$,则体积的最大值为$${{(}{)}}$$
A
A.$$( {\frac{1} {6}} )^{3} \pi$$
B.$$( {\frac{1} {3}} )^{3} \pi$$
C.$$( \frac{1} {4} )^{3} \pi$$
D.$$( \frac{1} {2} )^{3} \pi$$
6、['棱锥的结构特征及其性质', '导数与最值', '利用导数解决实际应用问题', '棱柱、棱锥、棱台的侧面积与表面积']正确率40.0%如图所示,一个仓库设计由上部屋顶和下部主体两部分组成,屋顶的形状是四棱锥$$P-A B C D$$,四边形$${{A}{B}{C}{D}}$$是正方形,点$${{O}}$$为正方形$${{A}{B}{C}{D}}$$的中心,$${{P}{O}{⊥}}$$平面$${{A}{B}{C}{D}}$$;下部的形状是长方体$$A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$.已知上部屋顶造价与屋顶面积成正比,比例系数为$$k ( k > 0 )$$,下部主体造价与其高度成正比,比例系数为$${{8}{k}}$$.若欲造一个上$${、}$$下总高度为$$1 0 ~ \mathrm{m}, ~ A B=8 ~ \mathrm{m}$$的仓库,则当总造价最低时,$${{P}{O}{=}}$$()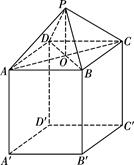
B
A.$$\frac{4 \sqrt{5}} {5} m$$
B.$$\frac{4 \sqrt{3}} {3} m$$
C.$${{4}{m}}$$
D.$${{4}{\sqrt {5}}{m}}$$
7、['变化率', '基本初等函数的导数', '利用导数解决实际应用问题', '瞬时变化率']正确率60.0%一物体的运动方程是$$S=-\frac{1} {2} a t^{2} \wedge a$$为常数),则该物体在$${{t}{=}{{t}_{0}}}$$时刻的瞬时速度为()
B
A.$${{a}{{t}_{0}}}$$
B.$${{−}{a}{{t}_{0}}}$$
C.$${\frac{1} {2}} a t_{0}$$
D.$${{2}{a}{{t}_{0}}}$$
8、['导数与最值', '利用导数解决实际应用问题']正确率40.0%某产品的销售收入$${{y}_{1}{(}}$$万元$${{)}}$$是产量$${{x}{(}}$$千台$${{)}}$$的函数,且函数解析式为$$y_{1}=1 7 x^{2} ( x > 0 )$$,生产成本$${{y}_{2}{(}}$$万元$${{)}}$$是产量$${{x}{(}}$$千台$${{)}}$$的函数,且函数解析式为$$y_{2}=2 x^{3}-x^{2} ( x > 0 )$$,要使利润最大,则该产品应生产$${{(}{)}}$$
A
A.$${{6}}$$千台
B.$${{7}}$$千台
C.$${{8}}$$千台
D.$${{9}}$$千台
9、['利用导数解决实际应用问题']正确率80.0%某厂生产$${{x}}$$件产品的总成本为$${{C}}$$万元,产品单价为$${{P}}$$万元,且满足$$C=1 2 0 0+\frac{2} {7 5} x^{3}$$,$$P=\frac{5 0 0} {\sqrt{x}}$$,则总利润最大时,$${{x}{=}{(}{)}}$$
A
A.$${{2}{5}}$$
B.$${{2}{6}}$$
C.$${{2}{4}}$$
D.$${{2}{8}}$$
10、['利用导数解决实际应用问题']正确率80.0%已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=2-|x+2|.若对任意的x∈[-1,2],f(x+a)>f(x)成立,则实数a的取值范围是( )
A.(0,2)
B.(0,2)∪(-∞,-6)
C.(-2,0)
D.(-2,0)∪(6,+∞)
1. 解析:
设燃料费与速度的关系为 $$F = kv^3$$,由题意当 $$v = 10$$ 时 $$F = 25$$,代入得 $$k = \frac{25}{1000} = \frac{1}{40}$$。总费用为燃料费与固定费用之和乘以时间:
$$C(v) = \left(\frac{v^3}{40} + 400\right) \cdot \frac{800}{v} = \frac{800v^2}{40} + \frac{400 \times 800}{v} = 20v^2 + \frac{320000}{v}$$
求导并令导数为零:
$$C'(v) = 40v - \frac{320000}{v^2} = 0 \Rightarrow 40v^3 = 320000 \Rightarrow v^3 = 8000 \Rightarrow v = 20$$
验证 $$v = 20$$ 是最小值点,因此答案为 C。
2. 解析:
设下底长为 $$x$$,高为 $$h$$。由等腰梯形性质,两腰与下底的垂线段长度为 $$\frac{x - 7}{2}$$,根据勾股定理:
$$h = \sqrt{2^2 - \left(\frac{x - 7}{2}\right)^2} = \sqrt{4 - \frac{(x - 7)^2}{4}}$$
面积为:
$$A = \frac{7 + x}{2} \cdot \sqrt{4 - \frac{(x - 7)^2}{4}}$$
为简化计算,设 $$x = 7 + 2t$$,则:
$$A = (7 + t) \sqrt{4 - t^2}$$
求导并令导数为零,解得 $$t = 1$$,即 $$x = 9$$。验证 $$x = 9$$ 是最大值点,因此答案为 D。
3. 解析:
设矩形在直径上的边长为 $$2a$$,则另一边长为 $$\sqrt{R^2 - a^2}$$。周长为:
$$P = 2(2a + \sqrt{R^2 - a^2})$$
求导并令导数为零:
$$P'(a) = 2\left(2 - \frac{a}{\sqrt{R^2 - a^2}}\right) = 0 \Rightarrow 2 = \frac{a}{\sqrt{R^2 - a^2}} \Rightarrow 4(R^2 - a^2) = a^2 \Rightarrow a = \frac{2R}{\sqrt{5}}$$
因此矩形边长为 $$\frac{4R}{\sqrt{5}}$$ 和 $$\frac{R}{\sqrt{5}}$$,即 $$\frac{4\sqrt{5}}{5}R$$ 和 $$\frac{\sqrt{5}}{5}R$$,答案为 B。
4. 解析:
油耗为每小时的耗油量乘以时间:
$$C(x) = \left(\frac{x^3}{81000} - \frac{x}{10} + 18\right) \cdot \frac{200}{x} = \frac{200x^2}{81000} - 20 + \frac{3600}{x} = \frac{2x^2}{810} + \frac{3600}{x} - 20$$
求导并令导数为零:
$$C'(x) = \frac{4x}{810} - \frac{3600}{x^2} = 0 \Rightarrow \frac{4x^3}{810} = 3600 \Rightarrow x^3 = 729000 \Rightarrow x = 90$$
验证 $$x = 90$$ 是最小值点,因此答案为 C。
5. 解析:
设圆柱底面半径为 $$r$$,高为 $$h$$。轴截面周长为:
$$2(2r + h) = 1 \Rightarrow h = \frac{1}{2} - 2r$$
体积为:
$$V = \pi r^2 h = \pi r^2 \left(\frac{1}{2} - 2r\right) = \frac{\pi r^2}{2} - 2\pi r^3$$
求导并令导数为零:
$$V'(r) = \pi r - 6\pi r^2 = 0 \Rightarrow r = \frac{1}{6}$$
验证 $$r = \frac{1}{6}$$ 是最大值点,体积为 $$\pi \left(\frac{1}{6}\right)^2 \left(\frac{1}{2} - \frac{1}{3}\right) = \frac{\pi}{216} = \left(\frac{1}{6}\right)^3 \pi$$,答案为 A。
6. 解析:
设 $$PO = h$$,则下部高度为 $$10 - h$$。屋顶面积为正方形面积加四个三角形面积:
$$A_{\text{屋顶}} = 8^2 + 4 \cdot \frac{1}{2} \cdot 8 \cdot \sqrt{h^2 + 4^2}} = 64 + 16\sqrt{h^2 + 16}$$
总造价为:
$$C(h) = k(64 + 16\sqrt{h^2 + 16}) + 8k(10 - h)$$
求导并令导数为零:
$$C'(h) = k \cdot \frac{16h}{\sqrt{h^2 + 16}} - 8k = 0 \Rightarrow \frac{16h}{\sqrt{h^2 + 16}} = 8 \Rightarrow 2h = \sqrt{h^2 + 16} \Rightarrow 4h^2 = h^2 + 16 \Rightarrow h = \frac{4\sqrt{3}}{3}$$
验证 $$h = \frac{4\sqrt{3}}{3}$$ 是最小值点,答案为 B。
7. 解析:
瞬时速度为运动方程的导数:
$$v(t) = \frac{dS}{dt} = \frac{d}{dt}\left(-\frac{1}{2} a t^2\right) = -a t$$
在 $$t = t_0$$ 时,速度为 $$-a t_0$$,答案为 B。
8. 解析:
利润为收入减去成本:
$$L(x) = 17x^2 - (2x^3 - x^2) = 18x^2 - 2x^3$$
求导并令导数为零:
$$L'(x) = 36x - 6x^2 = 0 \Rightarrow x = 6$$
验证 $$x = 6$$ 是最大值点,答案为 A。
9. 解析:
总利润为收入减去成本:
$$L(x) = P \cdot x - C = \frac{500}{\sqrt{x}} \cdot x - \left(1200 + \frac{2}{75}x^3\right) = 500\sqrt{x} - 1200 - \frac{2}{75}x^3$$
求导并令导数为零:
$$L'(x) = \frac{250}{\sqrt{x}} - \frac{6}{75}x^2 = 0 \Rightarrow \frac{250}{\sqrt{x}} = \frac{2}{25}x^2 \Rightarrow 6250 = 2x^{2.5} \Rightarrow x = 25$$
验证 $$x = 25$$ 是最大值点,答案为 A。
10. 解析:
由奇函数性质,当 $$x > 0$$ 时 $$f(x) = -2 + |x - 2|$$。函数在 $$[-1, 2]$$ 上的图像分为三段:
- $$x \in [-1, 0)$$:$$f(x) = 2 - |x + 2|$$,单调递减;
- $$x \in [0, 2]$$:$$f(x) = -2 + |x - 2|$$,单调递增。
要使 $$f(x + a) > f(x)$$ 对所有 $$x \in [-1, 2]$$ 成立,需 $$a > 0$$ 且 $$x + a$$ 超出 $$[-1, 2]$$ 或 $$a$$ 足够大。解得 $$a > 6$$ 或 $$0 < a < 2$$,答案为 B。
.jpg)