正确率40.0%已知$$a=\frac{3 2 ( 4-\operatorname{l n} 3 2 )} {e^{4}}$$,$$b=\frac{1} {e}$$,$$c=\frac{\operatorname{l o g}_{\sqrt e} 2} {4}$$,则$${{(}{)}}$$
A.$$a < c < b$$
B.$$c < a < b$$
C.$$a < b < c$$
D.$$b < a < c$$
2、['正弦(型)函数的单调性', '导数与单调性', '导数与最值', '特殊角的三角函数值']正确率40.0%函数$$y=x+2 \operatorname{c o s} x-\sqrt{3}$$在区间$$[ 0, \frac{\pi} {2} \Big]$$上的最大值是()
B
A.$$\frac{\pi} {2}-\sqrt{3}$$
B.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
C.$${{2}{−}{\sqrt {3}}}$$
D.$${{1}{−}{\sqrt {3}}}$$
3、['导数与单调性']正确率40.0%已知函数$$y=f ( x )$$,若$$f ( x ) > 0$$且$$f^{\prime} ( x )+x f ( x ) > 0$$,则有$${{(}{)}}$$
D
A.$${{f}{(}{x}{)}}$$可能是奇函数,也可能是偶函数
B.$$f (-1 ) > f ( 1 )$$
C.$$\frac{\pi} {4} < x < \frac{\pi} {2}$$时,$$f ( \operatorname{s i n} x ) < e^{\frac{\operatorname{c o s} 2 x} {2}} f ( \operatorname{c o s} x )$$
D.$$f ( 0 ) < \sqrt{e} f ( 1 )$$
4、['导数与单调性', '函数奇、偶性的定义', '函数图象的识别']正确率60.0%已知$$f ( x )=\frac{1} {2} x-\mathrm{s i n} x,$$则$${{f}{(}{x}{)}}$$的图像大致是()
A
A.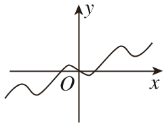
B.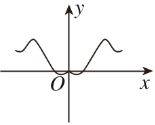
C.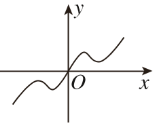
D.
正确率60.0%已知函数$$y=x f^{\prime} ( x )$$的图象如图所示(其中$$f^{\prime} ( x )$$是函数$${{f}{(}{x}{)}}$$的导函数)$${{.}}$$下面四个图象中$$y=f ( x )$$的图象大致是()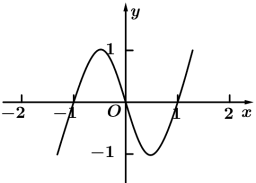
C
A.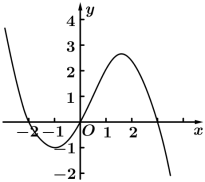
B.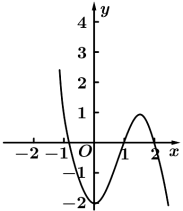
C.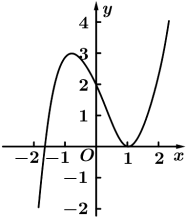
D.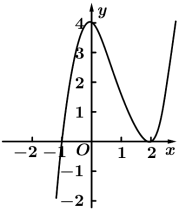
正确率40.0%已知函数$$f ( x )=\left\{\begin{array} {l l} {\operatorname{l o g}_{2} ( 1-x )+1,} & {1 \leqslant x \leqslant k,} \\ {x^{3}-3 x+2,} & {k < x \leqslant a,} \\ \end{array} \right.$$,若存在$${{k}}$$使得函数$${{f}{(}{x}{)}}$$的值域是$$[ 0, 2 ] \;,$$则实数$${{a}}$$的取值范围是()
B
A.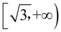
B.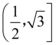
C.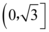
D.$${{\{}{2}{\}}}$$
7、['导数与单调性', '利用导数讨论函数单调性']正确率40.0%若函数$$f \left( x \right)=x^{3}-m x^{2}-x+5$$在区间$$( 0, 1 )$$内单调递减,则实数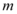 的取值范围是()
的取值范围是()
A
A.$${{m}{⩾}{1}}$$
B.$${{m}{>}{1}}$$
C.$${{m}{⩽}{1}}$$
D.$${{m}{<}{1}}$$
8、['导数与单调性']正确率40.0%已知$${{f}{(}{x}{)}}$$为定义在$$(-\infty, 0 ) \cup( 0,+\infty)$$上的偶函数,$$f^{\prime} ( x )$$是$${{f}{(}{x}{)}}$$的导函数,若当$${{x}{>}{0}}$$时,$$f^{\prime} ( x ) \operatorname{l n} x+\frac{f ( x )} {x} < 0$$,则不等式$$( x-1 ) f ( x ) < 0$$的解集是$${{(}{)}}$$
A
A.$$( 1,+\infty)$$
B.$$( 0, 1 )$$
C.$$(-\infty, 0 ) \cup( 1,+\infty)$$
D.$$(-\infty, 0 )$$
9、['导数与单调性']正确率40.0%已知函数$${{f}{(}{x}{)}}$$的定义域为$$(-\frac{\pi} {2}, \frac{\pi} {2} )$$,其导函数是$$f^{\prime} ( x )$$,有$$f^{\prime} ( x ) \operatorname{c o s} x+f ( x ) \operatorname{s i n} x < 0$$,则关于$${{x}}$$的不等式$$\sqrt{3} f ( x ) < 2 f ( \frac{\pi} {6} ) \operatorname{c o s} x$$的解集为$${{(}{)}}$$
B
A.$$( \frac{\pi} {3}, \frac{\pi} {2} )$$
B.$$( \frac{\pi} {6}, \frac{\pi} {2} )$$
C.$$(-\frac{\pi} {6},-\frac{\pi} {3} )$$
D.$$(-\frac{\pi} {2},-\frac{\pi} {6} )$$
10、['导数与单调性']正确率60.0%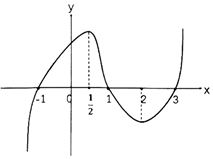 已知$$y=( 1-x ) f^{\prime} ( x )$$的图象如图所示,其中$$f^{\prime} ( x )$$是函数$${{f}{(}{x}{)}}$$的导数,则所给选项的四个图象中,函数$$y=f ( x )$$的图象可能是$${{(}{)}}$$
已知$$y=( 1-x ) f^{\prime} ( x )$$的图象如图所示,其中$$f^{\prime} ( x )$$是函数$${{f}{(}{x}{)}}$$的导数,则所给选项的四个图象中,函数$$y=f ( x )$$的图象可能是$${{(}{)}}$$
B
A.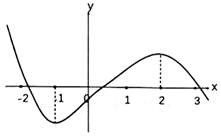
B.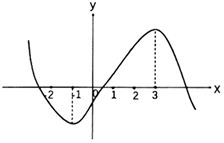
C.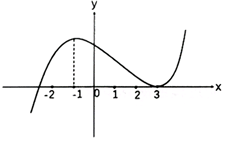
D.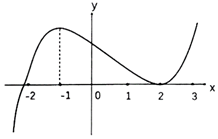
1. 比较 $$a$$, $$b$$, $$c$$ 的大小关系:
- $$a = \frac{32(4 - \ln 32)}{e^4}$$,其中 $$\ln 32 \approx 3.4657$$,故 $$4 - \ln 32 \approx 0.5343$$,$$e^4 \approx 54.598$$,因此 $$a \approx \frac{32 \times 0.5343}{54.598} \approx 0.313$$。
- $$b = \frac{1}{e} \approx 0.3679$$。
- $$c = \frac{\log_{\sqrt{e}} 2}{4} = \frac{\ln 2}{\frac{1}{2} \ln e} \times \frac{1}{4} = \frac{\ln 2}{2} \approx 0.3466$$。
2. 求函数 $$y = x + 2 \cos x - \sqrt{3}$$ 在区间 $$[0, \frac{\pi}{2}]$$ 上的最大值:
- $$y(0) = 0 + 2 \times 1 - \sqrt{3} = 2 - \sqrt{3} \approx 0.2679$$。
- $$y\left(\frac{\pi}{6}\right) = \frac{\pi}{6} + 2 \times \frac{\sqrt{3}}{2} - \sqrt{3} = \frac{\pi}{6} \approx 0.5236$$。
- $$y\left(\frac{\pi}{2}\right) = \frac{\pi}{2} + 0 - \sqrt{3} \approx 1.5708 - 1.732 \approx -0.161$$。
3. 分析函数 $$f(x)$$ 的性质:
- 选项 B:由 $$g(-1) < g(1)$$,得 $$f(-1) < e f(1)$$,但无法直接推出 $$f(-1) > f(1)$$,排除。
- 选项 C:当 $$\frac{\pi}{4} < x < \frac{\pi}{2}$$,$$\sin x < \cos x$$,由 $$g(\sin x) < g(\cos x)$$,得 $$f(\sin x) < e^{(\cos^2 x - \sin^2 x)/2} f(\cos x) = e^{\cos 2x / 2} f(\cos x)$$,正确。
- 选项 D:由 $$g(0) < g(1)$$,得 $$f(0) < e^{1/2} f(1) = \sqrt{e} f(1)$$,正确。
4. 函数 $$f(x) = \frac{1}{2} x - \sin x$$ 的图像分析:
- 当 $$x \in (-\frac{\pi}{3}, \frac{\pi}{3})$$,$$f'(x) < 0$$,函数递减;
- 当 $$x \in (\frac{\pi}{3}, \pi)$$,$$f'(x) > 0$$,函数递增。
5. 由 $$y = x f'(x)$$ 的图像推导 $$f(x)$$ 的图像:
- 当 $$x < 0$$,$$f'(x)$$ 与 $$y$$ 同号;
- 当 $$x > 0$$,$$f'(x)$$ 与 $$y$$ 同号。
6. 函数 $$f(x)$$ 的值域为 $$[0, 2]$$,求 $$a$$ 的取值范围:
- 当 $$1 \leq x \leq k$$,$$f(x) = \log_2 (1 - x) + 1$$,需满足 $$f(k) = 0$$,解得 $$k = 0$$(不满足 $$k \geq 1$$),故无解。
- 当 $$k < x \leq a$$,$$f(x) = x^3 - 3x + 2$$,需满足 $$f(a) = 2$$,解得 $$a = 0$$ 或 $$a = 1$$ 或 $$a = 2$$。
7. 函数 $$f(x) = x^3 - m x^2 - x + 5$$ 在 $$(0, 1)$$ 内单调递减,求 $$m$$ 的取值范围:
8. 不等式 $$(x - 1) f(x) < 0$$ 的解集:
- 当 $$x > 1$$,$$\ln x > 0$$,由 $$g(x) < g(1) = 0$$,得 $$f(x) < 0$$;
- 当 $$0 < x < 1$$,$$\ln x < 0$$,由 $$g(x) > g(1) = 0$$,得 $$f(x) < 0$$;
- 由偶性,$$f(-x) = f(x)$$。
9. 不等式 $$\sqrt{3} f(x) < 2 f\left(\frac{\pi}{6}\right) \cos x$$ 的解集:
10. 由 $$y = (1 - x) f'(x)$$ 的图像推导 $$f(x)$$ 的图像:
- 当 $$x < 0$$,$$f'(x)$$ 与 $$y$$ 异号;
- 当 $$0 < x < 1$$,$$f'(x)$$ 与 $$y$$ 同号;
- 当 $$x > 1$$,$$f'(x)$$ 与 $$y$$ 异号。
.jpg)