正确率40.0%已知函数$$f ( x )=\frac{1+\operatorname{l n} x} {x},$$则$${{f}{(}{x}{)}}$$在区间$$\left( a, \ a+\frac{2} {3} \right) ( a > 0 )$$上存在极值的一个充分不必要条件是()
A
A.$$\left( \frac{2} {3}, \, 1 \right)$$
B.$$\left( 0, \ \frac{2} {3} \right)$$
C.$$\left( 0, \enspace\frac{1} {3} \right)$$
D.$$\left( \frac{1} {3}, \, 1 \right)$$
2、['导数与单调性', '导数与极值']正确率40.0%已知$$f^{\prime} ( x )$$是函数$${{f}{(}{x}{)}}$$在$${{R}}$$上的导函数,且函数$${{f}{(}{x}{)}}$$在$${{x}{=}{−}{2}}$$处取得极小值,则函数$$y=x f^{\prime} ( x )$$的图象可能是()
A
A.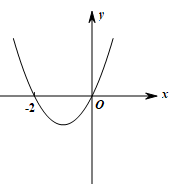
B.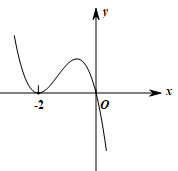
C.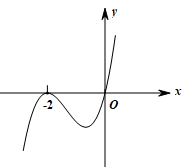
D.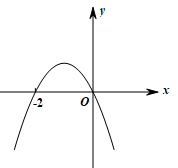
正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=x l n x$$,则$${{f}{(}{x}{)}}$$极小值为()
C
A.$$\frac{1} {e}$$
B.$${{e}}$$
C.$$- \frac{1} {e}$$
D.$${{−}{e}}$$
4、['导数与极值', '利用导数求参数的取值范围', '二次函数的图象分析与判断']正确率60.0%已知函数$$f ( x )=\frac{1} {3} x^{3}-m x^{2}+x+2$$有两个极值点,则实数$${{m}}$$的取值范围是()
D
A.$$(-1, ~ 1 )$$
B.$$[-1, ~ 1 ]$$
C.$$(-\infty, ~-1 ] \cup[ 1, ~+\infty)$$
D.$$(-\infty, ~-1 ) \cup( 1, ~+\infty)$$
5、['导数与极值', '函数单调性的判断', '函数的单调区间']正确率80.0%函数$$y=f ( x )$$导函数$$f^{\prime} ( x )$$的图象如图所示,则下列说法正确的是()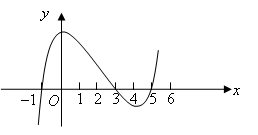
D
A.函数$$y=f ( x )$$在$$(-\infty, 0 )$$上单调递增
B.函数$$y=f ( x )$$的递减区间为$$( 3, 5 )$$
C.函数$$y=f ( x )$$在$${{x}{=}{0}}$$处取得极大值
D.函数$$y=f ( x )$$在$${{x}{=}{5}}$$处取得极小值
6、['函数奇偶性的应用', '导数与极值', '函数求解析式']正确率40.0%已知函数 是$${{R}}$$
是$${{R}}$$
C
A.$${{−}{2}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{0}}$$
7、['导数的四则运算法则', '基本初等函数的导数', '导数与极值', '利用导数讨论函数单调性', '导数中的函数构造问题']正确率40.0%若函数$$f ( x )=e^{-x}+t l n x$$有两个极值点,则$${{t}}$$的取值范围为()
A
A.$$\left( 0, \frac{1} {e} \right)$$
B.$$\left(-\infty, \frac{1} {e} \right)$$
C.$$\left(-\frac{1} {e}, 0 \right)$$
D.$$\left( \frac{1} {e},+\infty\right)$$
8、['导数与极值']正确率60.0%若$$\operatorname* {l i m}_{\Delta x \to0} \frac{f ( x_{0}+\Delta x )-f ( x_{0} )} {\Delta x}=k,$$则$$\operatorname* {l i m}_{\Delta x \to0} \frac{f ( x_{0}+2 \cdot\Delta x )-f ( x_{0} )} {\triangle x}$$等于()
A
A.$${{2}{k}}$$
B.$${{k}}$$
C.$$\frac{1} {2} k$$
D.以上都不是
9、['导数与极值']正确率40.0%设$$x=-\frac{1} {2}$$是函数$$f ( x )=\operatorname{l n} ( x+2 )-a x^{2}-3 a^{2} x$$的极小值点,则$${{f}{(}{x}{)}}$$的极大值为()
D
A.$${{2}}$$
B.$${{1}}$$
C.$$\frac{3} {4}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
10、['导数与极值']正确率80.0%函数$$y=x+2 \operatorname{c o s} x$$在$$[ 0, \frac{\pi} {2} ]$$上的极大值点为$${{(}{)}}$$
C
A.$$( \frac{\pi} {6}, \frac{\pi} {6}+\sqrt{3} )$$
B.$$\frac{\pi} {3}$$
C.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
D.$$\frac{\pi} {2}$$
1. 首先求函数 $$f(x) = \frac{1 + \ln x}{x}$$ 的导数:
极值点满足 $$f'(x) = 0$$,即 $$\ln x = 0$$,解得 $$x = 1$$。为了在区间 $$\left(a, a + \frac{2}{3}\right)$$ 上存在极值,需要 $$1 \in \left(a, a + \frac{2}{3}\right)$$,即 $$a < 1 < a + \frac{2}{3}$$,解得 $$\frac{1}{3} < a < 1$$。题目要求充分不必要条件,因此选项 D $$\left(\frac{1}{3}, 1\right)$$ 符合。
2. 函数 $$f(x)$$ 在 $$x = -2$$ 处取得极小值,故 $$f'(-2) = 0$$,且在 $$x = -2$$ 左侧导数小于 0,右侧导数大于 0。考虑函数 $$y = x f'(x)$$:
观察选项,只有选项 C 符合这一特征。
3. 函数 $$f(x) = x \ln x$$ 的导数为:
令 $$f'(x) = 0$$,解得 $$x = \frac{1}{e}$$。当 $$x < \frac{1}{e}$$ 时,$$f'(x) < 0$$;当 $$x > \frac{1}{e}$$ 时,$$f'(x) > 0$$,故 $$x = \frac{1}{e}$$ 是极小值点。极小值为:
选项 C 正确。
4. 函数 $$f(x) = \frac{1}{3}x^3 - m x^2 + x + 2$$ 的导数为:
有两个极值点等价于 $$f'(x) = 0$$ 有两个不同的实数解,即判别式大于 0:
选项 D 正确。
5. 根据导函数图像:
但题目要求选择一个正确选项,可能是 B。
6. 题目不完整,无法解析。
7. 函数 $$f(x) = e^{-x} + t \ln x$$ 的导数为:
有两个极值点等价于 $$f'(x) = 0$$ 有两个解,即 $$\frac{t}{x} = e^{-x}$$ 有两个解。设 $$g(x) = x e^{-x}$$,则需 $$t$$ 为 $$g(x)$$ 的极大值。$$g'(x) = e^{-x} - x e^{-x} = e^{-x}(1 - x)$$,极大值在 $$x = 1$$ 处取得,$$g(1) = \frac{1}{e}$$。因此 $$t \in \left(0, \frac{1}{e}\right)$$,选项 A 正确。
8. 根据导数的定义:
选项 A 正确。
9. 函数 $$f(x) = \ln(x + 2) - a x^2 - 3a^2 x$$ 的导数为:
已知 $$x = -\frac{1}{2}$$ 是极小值点,故 $$f'\left(-\frac{1}{2}\right) = 0$$:
解得 $$a = \frac{1}{3}$$。再求 $$f(x)$$ 的极大值点:
令 $$f'(x) = 0$$,解得 $$x = 1$$。验证 $$x = 1$$ 为极大值点,极大值为:
但选项中没有此结果,可能是题目描述有误。
10. 函数 $$y = x + 2 \cos x$$ 的导数为:
令 $$y' = 0$$,解得 $$\sin x = \frac{1}{2}$$,即 $$x = \frac{\pi}{6}$$。验证 $$x = \frac{\pi}{6}$$ 为极大值点,选项 C 正确。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)