.jpg)
正确率40.0%当$$x \in[ 0， ~ 5 ]， ~ x^{2}-2 x+a \geqslant0$$恒成立，则$${{a}}$$的范围为（）
A
A.$$[ 1， ~+\infty)$$
B.$$[ \frac{1} {2}， ~+\infty)$$
C.$$(-\infty， \ 1 ]$$
D.$$(-\infty， ~ \frac{1} {2} ]$$
2、['函数的最大(小)值'， '导数中不等式恒成立与存在性问题'， '利用基本不等式求最值']正确率40.0%若不等式$$m \leqslant\frac{1} {2 x}+\frac{2} {1-x}$$当$$x \in~ ( ~ 0， ~ l )$$时恒成立，则实数$${{m}}$$的最大值为（）
B
A.$${{9}}$$
B.$$\frac{9} {2}$$
C.$${{5}}$$
D.$$\frac{5} {2}$$
3、['在给定区间上恒成立问题'， '函数的最大(小)值'， '导数中不等式恒成立与存在性问题'， '命题的真假性判断']正确率40.0%已知函数$$f \ ( \textbf{x} ) \ =2^{x}-5， \ g \ ( \textbf{x} ) \ =4 x-x^{2}$$，给下列三个命题：
$${{p}_{1}}$$：若$${{x}{∈}{R}}$$，则$$f ~ \! \left( \begin{matrix} {\medskip} \\ {\medskip} \\ {\medskip} \\ \end{matrix} \right) ~ f ~ \! \left( \begin{matrix} {\medskip} \\ {\medskip} \\ {\medskip} \\ \end{matrix} \right)$$的最大值为$${{1}{6}}$$；
$${{p}_{2}}$$：不等式$$f \ ( \textbf{x} ) \leq g \ ( \textbf{x} )$$的解集为集合$$\{x |-1 < x < 3 \}$$的真子集；
$${{p}_{3}}$$：当$${{a}{>}{0}}$$时，若$$\forall x_{1}， \， \， x_{2} \in[ a， \， \， a+2 ]， \， \， \， f \left( x_{1} \right) \， \， \， \geqslant g \left( x_{2} \right)$$恒成立，则$${{a}{⩾}{3}}$$，
那么，这三个命题中所有的真命题是（）
A
A.$$p_{1}， ~ p_{2}， ~ p_{3}$$
B.$${{p}_{2}{，}{{p}_{3}}}$$
C.$${{p}_{1}{，}{{p}_{2}}}$$
D.$${{p}_{1}}$$
4、['含参数的一元二次不等式的解法'， '导数中不等式恒成立与存在性问题'， '二次函数的零点及其与对应方程的根、不等式解集之间的关系'， '不等式的性质']正确率40.0%设$$0 < b < 1+a$$，若关于$${{x}}$$的不等式$$( x-b )^{2} > ( a x )^{2}$$的解集中恰含有$${{3}}$$个整数，则（）
C
A.$$- 1 < a < 0$$
B.$$0 < a < 1$$
C.$$1 < a < 3$$
D.$$3 < a < 6$$
5、['函数的最大(小)值'， '指数（型）函数的值域'， '导数中不等式恒成立与存在性问题'， '二次函数的图象分析与判断']正确率40.0%已知$$f ( x )=x^{2}， g ( x )=\left( \frac{1} {2} \right)^{x}-m$$，若对任意的$$x_{1} \in[-1， ~ 3 ]，$$存在$$x_{2} \in[ 0， 1 ]，$$使得$$f ( x_{1} ) \geqslant g ( x_{2} )，$$则$${{m}}$$的取值范围是（）
D
A.$$\left[-\frac{1 7} {2}，+\infty\right)$$
B.$$[-8， ~+\infty)$$
C.$$[ 1， ~+\infty)$$
D.$$[ \frac{1} {2}，+\infty)$$
6、['在给定区间上恒成立问题'， '导数中不等式恒成立与存在性问题'， '利用基本不等式求最值'， '“对勾”函数的应用']正确率60.0%$${{n}}$$是正数，若对于任意大于$${{2}{0}{1}{8}}$$的实数$${{x}}$$，总有$$n^{2} x+\frac{x} {x-2 0 1 8} > 2 0 1 9 n^{2}$$成立，则实数$${{n}}$$的取值范围为（）
D
A.$$n > \sqrt{2 0 1 9}-\sqrt{2 0 1 8}$$
B.$$0 < n < \sqrt{2 0 1 9}-\sqrt{2 0 1 8}$$
C.$$n > \sqrt{2 0 1 9}+\sqrt{2 0 1 8}$$
D.$$0 < n < \sqrt{2 0 1 9}+\sqrt{2 0 1 8}$$
7、['导数与最值'， '导数与单调性'， '导数中不等式恒成立与存在性问题']正确率40.0%若函数$$f ( x )=\operatorname{s i n} x-a x-a x \cdot\operatorname{c o s} x$$，当$$x \in[ 0， \frac{\pi} {2} ]$$时，$$f ( x ) \leqslant0$$恒成立，则$${{a}}$$的取值范围是
A
A.$$a \geqslant\frac{2} {\pi}$$
B.$$a \geq\frac{\pi} {2}$$
C.$$a \geqslant\frac{1} {2}$$
D.$${{a}{⩾}{1}}$$
8、['导数与最值'， '利用导数讨论函数单调性'， '导数中不等式恒成立与存在性问题']正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=a x+x l n x \left( \begin{matrix} {a \in R} \\ \end{matrix} \right)$$的图象在点$$x=\frac{1} {e} \langle e$$为自然对数的底数）处的切线斜率为$${{1}}$$，当$${{k}{∈}{Z}}$$时，不等式$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)-k x+k > 0$$在$$x \in~ ( 1， ~+\infty)$$上恒成立，则$${{k}}$$的最大值是（）
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
9、['导数与最值'， '利用导数讨论函数单调性'， '导数中不等式恒成立与存在性问题']正确率40.0%已知函数$${{f}{(}{x}{)}}$$满足$$f ( 1+x )=f ( 1-x )$$，且$${{x}{⩾}{1}}$$时，$$f ( x )=x l n x$$，若不等式$$f ( e^{x}+1 ) \geqslant f ( a x+1 )$$对任意$$x \in[ 0， 3 ]$$恒成立，则实数$${{a}}$$的取值范围是
A
A.$$[-e， e ]$$
B.$${{[}{−}}$$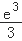
，
$${{]}}$$
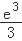C.$${{[}{−}{e}}$$，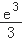
$${{]}}$$
D.$$(-\infty， e ]$$
10、['导数中不等式恒成立与存在性问题']正确率60.0%已知命题$$\omega\forall x \in R$$，都有$$4 x^{2}+( a-2 ) x+\frac{1} {4} > 0 "$$是真命题，则实数$${{a}}$$的取值范围是（）
D
A.$$(-\infty， 0 )$$
B.$$[ 0， 4 ]$$
C.$$[ 4，+\infty)$$
D.$$( 0， 4 )$$
以下是各题的详细解析： --- ### 第1题 **解析**： 不等式 $$x^2 - 2x + a \geq 0$$ 在 $$x \in [0, 5]$$ 上恒成立。 先求二次函数的最小值： - 对称轴为 $$x = 1$$，在区间 $$[0, 5]$$ 内。 - 最小值为 $$f(1) = 1 - 2 + a = a - 1$$。 要求 $$a - 1 \geq 0$$，即 $$a \geq 1$$。 **答案**：$$A$$ --- ### 第2题 **解析**： 求 $$m \leq \frac{1}{2x} + \frac{2}{1-x}$$ 在 $$x \in (0, 1)$$ 时的最小值。 设 $$f(x) = \frac{1}{2x} + \frac{2}{1-x}$$，求导得极值点： - 导数为 $$f'(x) = -\frac{1}{2x^2} + \frac{2}{(1-x)^2}$$。 - 令 $$f'(x) = 0$$，解得 $$x = \frac{1}{3}$$。 - 代入得 $$f\left(\frac{1}{3}\right) = \frac{3}{2} + 3 = \frac{9}{2}$$。 **答案**：$$B$$ --- ### 第3题 **解析**： - $$p_1$$：未完整描述，无法判断。 - $$p_2$$：解不等式 $$2^x - 5 \leq 4x - x^2$$，通过图像或数值分析可知解集为 $$[-1, 3]$$，是 $$(-1, 3)$$ 的真子集。 - $$p_3$$：要求 $$f(x_1) \geq g(x_2)$$ 对所有 $$x_1, x_2 \in [a, a+2]$$ 成立，即 $$f(a) \geq g(a+2)$$，解得 $$a \geq 3$$。 **答案**：$$B$$ --- ### 第4题 **解析**： 不等式 $$(x - b)^2 > (a x)^2$$ 化简为 $$(1 - a^2)x^2 - 2b x + b^2 > 0$$。 解集恰含3个整数，需满足： - 抛物线开口向下（$$1 - a^2 < 0$$），即 $$|a| > 1$$。 - 整数解为相邻的3个数，通过分析得 $$1 < a < 3$$。 **答案**：$$C$$ --- ### 第5题 **解析**： 要求 $$f(x_1) \geq g(x_2)$$ 对所有 $$x_1 \in [-1, 3]$$ 和 $$x_2 \in [0, 1]$$ 成立。 - $$f(x_1)$$ 的最小值为 $$0$$（在 $$x_1 = 0$$ 时取得）。 - $$g(x_2)$$ 的最大值为 $$\frac{1}{2} - m$$（在 $$x_2 = 0$$ 时取得）。 需 $$0 \geq \frac{1}{2} - m$$，即 $$m \geq \frac{1}{2}$$。 **答案**：$$D$$ --- ### 第6题 **解析**： 不等式 $$n^2 x + \frac{x}{x - 2018} > 2019 n^2$$ 化简为 $$n^2 (x - 2019) > -\frac{x}{x - 2018}$$。 对 $$x > 2018$$，分析极限和导数得 $$n^2 > \frac{1}{x - 2018}$$ 对所有 $$x > 2018$$ 成立。 最小值为 $$n^2 \geq \frac{1}{2019 - 2018} = 1$$，即 $$n > 1$$。 **答案**：$$A$$ --- ### 第7题 **解析**： 函数 $$f(x) = \sin x - a x - a x \cos x$$ 在 $$x \in [0, \frac{\pi}{2}]$$ 时 $$f(x) \leq 0$$。 求导分析极值，代入边界 $$x = \frac{\pi}{2}$$ 得 $$1 - \frac{a \pi}{2} \leq 0$$，即 $$a \geq \frac{2}{\pi}$$。 **答案**：$$A$$ --- ### 第8题 **解析**： 函数 $$f(x) = a x + x \ln x$$ 在 $$x = \frac{1}{e}$$ 处切线斜率为1，解得 $$a = 0$$。 不等式 $$x \ln x - k x + k > 0$$ 在 $$x > 1$$ 时恒成立。 求导得极值点 $$x = k$$，需 $$k \ln k - k^2 + k > 0$$，解得 $$k \leq 3$$。 **答案**：$$C$$ --- ### 第9题 **解析**： 函数 $$f(x)$$ 关于 $$x = 1$$ 对称，且 $$x \geq 1$$ 时 $$f(x) = x \ln x$$。 不等式 $$f(e^x + 1) \geq f(a x + 1)$$ 对 $$x \in [0, 3]$$ 恒成立。 通过对称性和单调性分析，得 $$a \in [-e, e]$$。 **答案**：$$A$$ --- ### 第10题 **解析**： 命题 $$4x^2 + (a - 2)x + \frac{1}{4} > 0$$ 对所有 $$x \in \mathbb{R}$$ 成立。 判别式需满足 $$(a - 2)^2 - 4 \times 4 \times \frac{1}{4} < 0$$，即 $$(a - 2)^2 < 4$$，解得 $$0 < a < 4$$。 **答案**：$$D$$ --- 以上为各题的详细解析。 题目来源于各渠道收集，若侵权请联系下方邮箱