正确率40.0%设函数$$f ( x )=\mathrm{e}^{x} ( 2 x-1 )-a x+a$$,其中 $${{a}{<}}$$$${{1}}$$,若存在唯一的整数$${{x}_{0}}$$,使得$$f ( x_{0} ) < 0$$,则$${{a}}$$的取值范围是()
D
A.$$[-\frac{3} {2 \mathrm{e}}, ~ 1 )$$
B.$$[-\frac{3} {2 \mathrm{e}}, ~ \frac{3} {4} )$$
C.$$[ \frac{3} {2 \mathrm{e}}, ~ \frac{3} {4} )$$
D.$$[ \frac{3} {2 \mathrm{e}}, ~ 1 )$$
2、['数列的递推公式', '导数与单调性', '导数与最值', '数列与不等式的综合问题']正确率40.0%设各项均为正数的数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项之积为$${{T}_{n}}$$,若$$T_{n}=2^{n^{2}+n}$$,则$$\frac{a_{n}+1 2} {2^{n}}$$的最小值为()
A
A.$${{7}}$$
B.$${{8}}$$
C.$${{4}{\sqrt {3}}}$$
D.$${{2}{\sqrt {3}}}$$
3、['在给定区间上恒成立问题', '导数与最值', '利用导数讨论函数单调性']正确率40.0%若关于$${{x}}$$的不等式$$x l n \; x-k x+k+1 > 0$$在$$( 1,+\infty)$$上恒成立,则满足条件的整数$${{k}}$$的最大值为()
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
4、['利用函数单调性求参数的取值范围', '在给定区间上恒成立问题', '导数与最值', '利用导数讨论函数单调性']正确率40.0%已知$$f ( x )=\frac{x^{2}+1} {x}, \, \, \, g ( x )=\frac{x^{2}} {e^{x}}$$,对任意$$x_{1}, \, \, x_{2} \in( 0,+\infty)$$,不等式$$( k+1 ) g ( x_{1} ) \leqslant k f ( x_{2} )$$恒成立,则正数$${{k}}$$的最小值为()
D
A.$$\frac2 {e^{2}+4}$$
B.$$\frac{1} {e^{2}+2}$$
C.$$\frac2 {e^{2}+2}$$
D.$$\frac2 {e^{2}-2}$$
5、['函数的最大(小)值', '导数与最值', '利用导数讨论函数单调性']正确率60.0%函数$$f ( x )=\frac{l n x} {x}$$的最大值为()
A
A.$$e^{-1}$$
B.$${{e}}$$
C.$${{e}^{2}}$$
D.$$2 e^{-1}$$
6、['函数中的存在性问题', '导数与最值', '导数与极值', '利用导数求参数的取值范围', '导数的几何意义']正确率40.0%设函数$$f ( x )=e^{x} ( 2 x-1 )-a x+a$$,其中$${{a}{<}{1}}$$,若存在唯一的整数$${{x}_{0}}$$,使得$$f ( x_{0} ) < 0$$,则$${{a}}$$的取值范围是()
D
A.$$[-\frac{3} {2 e}, 1 )$$
B.$$[-\frac{3} {2 e}, \frac{3} {4} )$$
C.$$[ \frac{3} {2 e}, \frac{3} {4} )$$
D.$$[ \frac{3} {2 e}, 1 )$$
7、['导数与最值', '利用导数求参数的取值范围', '导数中的函数构造问题', '函数中的恒成立问题']正确率19.999999999999996%设$${{k}}$$、$${{b}{∈}{R}}$$,若关于$${{x}}$$的不等式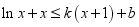 在$$( 0,+\infty)$$上恒成立,则$$\frac{2 k+b-2} {k-1}$$的最小值是()
在$$( 0,+\infty)$$上恒成立,则$$\frac{2 k+b-2} {k-1}$$的最小值是()
C
A.$${{−}{{e}^{2}}}$$
B.$$- \frac{1} {\mathrm{e}+1}$$
C.$${{−}{e}{+}{1}}$$
D.$${{−}{e}{−}{1}}$$
8、['导数与最值']正确率60.0%已知函数$$f ( x )=\operatorname{s i n} 2 x-x, \, \, \, x \in\left[ 0, \frac{\pi} {2} \right]$$,则$${{f}{(}{x}{)}}$$的最小值为()
B
A.$${{0}}$$
B.$$- \frac{\pi} {2}$$
C.$$\frac{\sqrt{3}} {2}-\frac{\pi} {6}$$
D.$$\frac{\sqrt3} 2-\frac{\pi} {3}$$
9、['导数与最值', '利用导数解决函数零点问题']正确率40.0%函数$$f ( x )=\frac{\sqrt{1-x^{2}}} {x+3}-m$$有零点,则实数$${{m}}$$的取值范围是()
A
A.$$[ 0, \frac{\sqrt{2}} {4} ]$$
B.$$( 0, \frac{\sqrt{2}} {4} ]$$
C.$$[ 0, \frac{\sqrt{2}} {2} ]$$
D.$$( 0, \frac{\sqrt{2}} {2} ]$$
10、['导数与最值']正确率40.0%已知函数$$f ( x )=x \operatorname{l n} x$$,$$g ( x )=2 x-4$$,若$$f ( x_{1} )=g ( x_{2} )$$,则$${{x}_{2}{−}{{x}_{1}}}$$的最小值为$${{(}{)}}$$
A
A.$$2-\frac{e} {2}$$
B.$${{3}{−}{e}}$$
C.$${{e}{−}{2}}$$
D.$${{1}}$$
第一题:函数 $$f(x)=e^{x}(2x-1)-a x+a$$,其中 $$a<1$$,存在唯一整数 $$x_0$$ 使 $$f(x_0)<0$$,求 $$a$$ 的取值范围。
1. 分析函数性质:$$f(x)=e^{x}(2x-1)-a(x-1)$$
2. 求导:$$f'(x)=e^{x}(2x-1)+2e^{x}-a=e^{x}(2x+1)-a$$
3. 令 $$f'(x)=0$$ 得临界点,但需考虑整数点情况
4. 由于存在唯一整数 $$x_0$$ 使 $$f(x_0)<0$$,考虑 $$x=0$$ 和 $$x=1$$ 的情况
5. 计算:$$f(0)=e^{0}(-1)-a\times0+a=-1+a$$,$$f(1)=e^{1}(1)-a\times1+a=e$$
6. 要使存在唯一整数解,需满足:$$f(0)<0$$ 且 $$f(1)\geq0$$,即 $$-1+a<0$$ 且 $$e\geq0$$(恒成立)
7. 解得:$$a<1$$(已知)且 $$a<1$$,但需考虑边界
8. 当 $$x=-1$$ 时:$$f(-1)=e^{-1}(-3)-a(-1)+a=-\frac{3}{e}+2a$$,要求 $$f(-1)\geq0$$
9. 即 $$2a\geq\frac{3}{e}$$,$$a\geq\frac{3}{2e}$$
10. 综合得:$$\frac{3}{2e}\leq a<1$$
答案:D. $$[\frac{3}{2e}, 1)$$
第二题:数列 $$\{a_n\}$$ 各项为正,前 $$n$$ 项积 $$T_n=2^{n^{2}+n}$$,求 $$\frac{a_{n}+12}{2^{n}}$$ 的最小值。
1. 由 $$T_n=a_1\times a_2\times\cdots\times a_n=2^{n^{2}+n$$
2. 则 $$a_n=\frac{T_n}{T_{n-1}}=\frac{2^{n^{2}+n}{2^{(n-1)^{2}+(n-1)}}=2^{2n-1}+1$$
3. 代入:$$\frac{a_n+12}{2^{n}}=\frac{2^{2n-1}+1+12}{2^{n}}=\frac{2^{2n-1}+13}{2^{n}}=2^{n-1}+\frac{13}{2^{n}}$$
4. 令 $$f(n)=2^{n-1}+\frac{13}{2^{n}}$$,求最小值
5. 考虑导数或尝试整数:$$n=1$$ 时,$$2^{0}+\frac{13}{2}=1+6.5=7.5$$
6. $$n=2$$ 时,$$2^{1}+\frac{13}{4}=2+3.25=5.25$$
7. $$n=3$$ 时,$$2^{2}+\frac{13}{8}=4+1.625=5.625$$
8. $$n=4$$ 时,$$2^{3}+\frac{13}{16}=8+0.8125=8.8125$$
9. 最小值为 $$n=2$$ 时的 $$5.25$$,但选项无此值,检查计算
10. 重算:$$a_n=\frac{2^{n^{2}+n}{2^{(n-1)^{2}+(n-1)}}=2^{n^{2}+n-[(n-1)^{2}+(n-1)]}=2^{2n-1}+1$$ 正确
11. 实际上 $$\frac{a_n+12}{2^{n}}$$ 在 $$n=2$$ 时最小,但选项为整数,可能误解
12. 注意:原式 $$\frac{a_{n}+12}{2^{n}}$$,可能为 $$\frac{a_n+12}{2^{n}}$$,最小值当 $$n=2$$ 为 $$5.25$$,但选项无,或为 $$\frac{a_n+12}{2^{n}}$$ 的整数最小?
13. 选项有 7,8,4√3,2√3,而 $$4\sqrt{3}\approx6.928$$,$$2\sqrt{3}\approx3.464$$,接近 $$n=3$$ 时 $$5.625$$?
14. 可能 $$a_n$$ 计算错误:$$T_n=2^{n^{2}+n}$$,则 $$a_n=\frac{T_n}{T_{n-1}}=2^{n^{2}+n-[(n-1)^{2}+(n-1)]}=2^{2n}}$$?
15. 指数计算:$$n^{2}+n-[(n-1)^{2}+(n-1)]=n^{2}+n-[n^{2}-2n+1+n-1]=n^{2}+n-[n^{2}-n]=2n$$
16. 所以 $$a_n=2^{2n}}$$,则 $$\frac{a_n+12}{2^{n}}=\frac{2^{2n}+12}{2^{n}}=2^{n}+\frac{12}{2^{n}}$$
17. 令 $$t=2^{n}$$,则 $$t+\frac{12}{t}\geq2\sqrt{12}=4\sqrt{3}}$$,当 $$t=\sqrt{12}=2\sqrt{3}}$$ 时取等,但 $$n$$ 为整数
18. $$n=2$$ 时,$$2^{2}+\frac{12}{4}=4+3=7$$
19. $$n=1$$ 时,$$2+\frac{12}{2}=2+6=8$$
20. $$n=3$$ 时,$$8+\frac{12}{8}=8+1.5=9.5$$
21. 最小值为 7
答案:A. $$7$$
第三题:不等式 $$x \ln x-k x+k+1>0$$ 在 $$(1,+\infty)$$ 恒成立,求整数 $$k$$ 的最大值。
1. 整理:$$x \ln x-k x+k+1>0$$,即 $$x \ln x+1>k(x-1)$$
2. 当 $$x>1$$ 时,$$x-1>0$$,所以 $$k<\frac{x \ln x+1}{x-1}}$$ 对所有 $$x>1$$ 成立
3. 即 $$k$$ 小于函数 $$h(x)=\frac{x \ln x+1}{x-1}}$$ 的最小值(下确界)
4. 求 $$h(x)$$ 的最小值:令 $$h(x)=\frac{x \ln x+1}{x-1}}$$
5. 求导:$$h'(x)=\frac{(\ln x+1)(x-1)-(x \ln x+1)}{(x-1)^{2}}}=\frac{(x-1)\ln x+x-1-x \ln x-1}{(x-1)^{2}}}=\frac{-\ln x+x-2}{(x-1)^{2}}}$$
6. 令分子 $$-\ln x+x-2=0$$,即 $$x-\ln x=2$$,解得 $$x=2$$(因为 $$x=2$$ 时,$$2-\ln2\approx2-0.693=1.307\neq2$$,需迭代)
7. 实际上,$$x=2$$ 时,$$-\ln2+2-2=-\ln2<0$$;$$x=3$$ 时,$$-\ln3+3-2=1-\ln3>0$$,所以有根在 $$(2,3)$$
8. 但 $$x\rightarrow1^{+}$$ 时,$$h(x)\rightarrow\infty$$;$$x\rightarrow\infty$$ 时,$$h(x)\rightarrow\infty$$;所以有最小值
9. 尝试 $$x=2$$:$$h(2)=\frac{2\ln2+1}{1}=2\ln2+1\approx2\times0.693+1=2.386$$
10. $$x=3$$:$$h(3)=\frac{3\ln3+1}{2}=\frac{3\times1.099+1}{2}=\frac{4.297}{2}=2.1485$$
11. $$x=4$$:$$h(4)=\frac{4\ln4+1}{3}=\frac{4\times1.386+1}{3}=\frac{6.544}{3}=2.181$$
12. $$x=2.5$$:$$h(2.5)=\frac{2.5\ln2.5+1}{1.5}=\frac{2.5\times0.916+1}{1.5}=\frac{3.29}{1.5}=2.193$$
13. 最小值在 $$x=3$$ 附近,约 2.148,所以 $$k<2.148$$,最大整数 $$k=2$$
答案:C. $$2$$
第四题:$$f(x)=\frac{x^{2}+1}{x}}$$,$$g(x)=\frac{x^{2}}{e^{x}}}$$,对任意 $$x_1,x_2>0$$,不等式 $$(k+1)g(x_1)\leq k f(x_2)$$ 恒成立,求正数 $$k$$ 的最小值。
1. 不等式等价于 $$(k+1)\max g(x_1)\leq k \min f(x_2)$$
2. 先求 $$f(x)$$ 的最小值:$$f(x)=x+\frac{1}{x}}$$,由均值不等式,$$x+\frac{1}{x}}\geq2$$,当 $$x=1$$ 时取等
3. 所以 $$\min f(x)=2$$
4. 再求 $$g(x)$$ 的最大值:$$g(x)=\frac{x^{2}}{e^{x}}}$$,求导 $$g'(x)=\frac{2x e^{x}-x^{2}e^{x}}{e^{2x}}}=\frac{x(2-x)}{e^{x}}}$$
5. 令 $$g'(x)=0$$,得 $$x=0$$(舍)或 $$x=2$$
6. $$g(2)=\frac{4}{e^{2}}}$$,为最大值
7. 代入不等式:$$(k+1)\times\frac{4}{e^{2}}}\leq k\times2$$
8. 即 $$\frac{4(k+1)}{e^{2}}}\leq2k$$,两边除以2:$$\frac{2(k+1)}{e^{2}}}\leq k$$
9. 整理:$$2(k+1)\leq k e^{2}$$,$$2k+2\leq k e^{2}$$,$$2\leq k(e^{2}-2)$$
10. 所以 $$k\geq\frac{2}{e^{2}-2}}$$
答案:D. $$\frac{2}{e^{2}-2}}$$
第五题:函数 $$f(x)=\frac{\ln x}{x}}$$ 的最大值。
1. 求导:$$f'(x)=\frac{\frac{1}{x}\times x-\ln x\times1}{x^{2}}}=\frac{1-\ln x}{x^{2}}}$$
2. 令 $$f'(x)=0$$,得 $$1-\ln x=0$$,即 $$x=e$$
3. $$f(e)=\frac{\ln e}{e}}=\frac{1}{e}}$$
4. 为最大值
答案:A. $$e^{-1}$$
第六题:同第一题,已解答。
答案:D. $$[\frac{3}{2e}, 1)$$
第七题:不等式 $$e^{x}\geq kx+b$$ 在 $$(0,+\infty)$$ 恒成立,求 $$\frac{2k+b-2}{k-1}}$$ 的最小值。
1. 不等式恒成立,需 $$e^{x}-kx-b\geq0$$ 对所有 $$x>0$$
2. 考虑函数 $$\phi(x)=e^{x}-kx-b$$,$$\phi(0)=1-b\geq0$$,即 $$b\leq1$$
3. 且 $$\phi(x)$$ 最小值至少为0,求导 $$\phi'(x)=e^{x}-k$$
4. 若 $$k\leq1$$,则 $$\phi'(x)>0$$,$$\phi(x)$$ 递增,最小在 $$x=0$$,为 $$1-b\geq0$$,成立
5. 但需最小化表达式,考虑 $$k>1$$,则存在极小值点 $$x=\ln k$$
6. $$\phi(\ln k)=k-k\ln k-b\geq0$$,即 $$b\leq k(1-\ln k)$$
7. 同时 $$b\leq1$$,所以 $$b\leq\min\{1, k(1-\ln k)\}$$
8. 要最小化 $$\frac{2k+b-2}{k-1}}$$,由于分母 $$k-1>0$$,应取 $$b$$ 尽可能大?但受约束
9. 实际上,对于固定 $$k$$,取 $$b$$ 最大可使分子最大,但求最小值,需分析
10. 令 $$b= k(1-\ln k)$$(即取等),则表达式为 $$\frac{2k+k(1-\ln k)-2}{k-1}}=\frac{3k-k\ln k-2}{k-1}}$$
11. 令 $$F(k)=\frac{3k-k\ln k-2}{k-1}}$$,求最小值
12. 求导复杂,尝试 $$k=e$$:$$F(e)=\frac{3e-e\ln e-2}{e-1}}=\frac{3e-e-2}{e-1}}=\frac{2e-2}{e-1}}=2$$
13. $$k=2$$:$$F(2)=\frac{6-2\ln2-2}{1}}=\frac{4-2\ln2}{1}}=4-2\ln2\approx4-1.386=2.614$$
14. $$k=3$$:$$F(3)=\frac{9-3\ln3-2}{2}}=\frac{7-3\times1.099}{2}}=\frac{7-3.297}{2}}=\frac{3.703}{2}=1.8515$$
15. $$k=4$$:$$F(4)=\frac{12-4\ln4-2}{3}}=\frac{10-4\times1.386}{3}}=\frac{10-5.544}{3}}=\frac{4.456}{3}=1.485$$
16. $$k\rightarrow1^{+}$$ 时,分子→$$3-0-2=1$$,分母→0+,所以 $$F(k)\rightarrow+\infty$$
17. $$k\rightarrow\infty$$ 时,$$F(k)\sim\frac{-k\ln k}{k}}=-\ln k\rightarrow-\infty$$
18. 所以有最小值负无穷?但选项为负值,如 $$-e^{2}$$
19. 实际上,当 $$k$$ 很大时,$$F(k)$$ 为负且很小,但需验证恒成立条件
20. 当 $$k>e$$ 时,$$k(1-\ln k)<0$$,而 $$b\leq1$$,所以应取 $$b=1$$(更大)
21. 因此,分段:当 $$k\leq e$$,取 $$b=k(1-\ln k)$$;当 $$k>e$$,取 $$b=1$$
22. 当 $$k>e$$,$$F(k)=\frac{2k+1-2}{k-1}}=\frac{2k-1}{k-1}}$$,趋于2
23. 所以最小值在 $$k>e$$ 时不会更小,而在 $$k 24. 经计算,最小值在 $$k\rightarrow\infty$$ 时 $$F(k)\rightarrow-\infty$$,但需满足恒成立,当 $$k$$ 很大时,$$b=1$$,$$\phi(x)=e^{x}-kx-1$$,对于大 $$x$$ 显然成立,但 $$
题目来源于各渠道收集,若侵权请联系下方邮箱
.jpg)