.jpg)
正确率40.0%设坐标原点为$${{O}}$$，抛物线$$y^{2}=4 x$$与过焦点的直线交于$${{A}{、}{B}}$$两点，则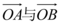
的夹角为（）
C
A.锐角
B.直角
C.钝角
D.无法确定
2、['抛物线的焦点弦问题']正确率80.0%过抛物线$$y^{2}=4 x$$的焦点$${{F}}$$作倾斜角为$${{3}{0}^{∘}}$$的直线交抛物线于$${{A}{，}{B}}$$两点，则$$| A B |=$$（）
A
A.$${{1}{6}}$$
B.$${{6}}$$
C.$${{1}{2}}$$
D.$${{7}{\sqrt {3}}}$$
3、['直线与抛物线的综合应用'， '抛物线的焦点弦问题']正确率40.0%过抛物线$${{C}}$$：$$y^{2}=8 x$$的焦点$${{F}}$$且斜率为$${\sqrt {3}}$$的直线与$${{C}}$$在第一象限的交点为$${{M}{，}{l}}$$为$${{C}}$$的准线，点$${{N}}$$在$${{l}}$$上且$$M N \perp l，$$则点$${{M}}$$到直线$${{N}{F}}$$的距离为（）
A
A.$${{4}{\sqrt {3}}}$$
B.$${{2}{\sqrt {6}}}$$
C.$$\sqrt{6}+4$$
D.$$4+\frac{4 \sqrt{6}} {3}$$
4、['抛物线的焦点弦问题']正确率60.0%已知$${{A}{，}{B}}$$是以$${{F}}$$为焦点的抛物线$$y^{2}=4 x$$上两点，且满足$$\overrightarrow{A F}=5 \overrightarrow{F B}，$$则弦$${{A}{B}}$$中点到准线距离为$${{(}{)}}$$
A
A.$$\frac{1 8} {5}$$
B.$$\frac{1 6} {5}$$
C.$$\frac{1 4} {5}$$
D.$$\frac{1 2} {5}$$
5、['直线的点斜式方程'， '抛物线的定义'， '抛物线的焦点弦问题']正确率40.0%设抛物线$$C : y^{2}=2 x$$的焦点为$${{F}}$$，过点$${{F}}$$且斜率为$$k \left( k > 0 \right)$$的直线$${{l}}$$与$${{C}}$$交于$${{A}{，}{B}}$$两点，$$| A B |=4$$，则直线$${{l}}$$的方程为
D
A.$$y=\sqrt{3} x-\frac{\sqrt{3}} {2}$$
B.$$y=2 x-1$$
C.$$y=x-1$$
D.$$y=x-\frac{1} {2}$$
6、['抛物线的顶点、焦点、准线'， '抛物线的焦点弦问题']正确率40.0%过抛物线$$C \colon~ y^{2}=2 p x ~ ( p > 0 )$$的焦点$${{F}}$$的直线交$${{C}}$$于$${{A}{，}{B}}$$两点，若$$| A F |=3 | B F |=3$$，则$${{p}{=}{（}}$$）
C
A.$${{3}}$$
B.$${{2}}$$
C.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
D.$${{1}}$$
7、['抛物线的顶点、焦点、准线'， '抛物线的对称性'， '抛物线的定义'， '抛物线的焦点弦问题']正确率40.0%已知抛物线$$y^{2}=4 x$$的焦点为$${{F}}$$，以$${{F}}$$为圆心的圆与抛物线交于$${{M}{、}{N}}$$两点，与抛物线的准线交于$${{P}{、}{Q}}$$两点，若四边形$${{M}{N}{P}{Q}}$$为矩形，则矩形$${{M}{N}{P}{Q}}$$的面积是（）
A
A.$${{1}{6}{\sqrt {3}}}$$
B.$${{1}{2}{\sqrt {3}}}$$
C.$${{4}{\sqrt {3}}}$$
D.$${{3}}$$
8、['平面上中点坐标公式'， '抛物线的定义'， '抛物线的焦点弦问题']正确率60.0%已知$${{A}{B}}$$是抛物线$$y^{2}=2 x$$的一条焦点弦，且$$| A B |=4$$，则$${{A}{B}}$$的中点$${{M}}$$的横坐标是（）
C
A.$${{2}}$$
B.$$\frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
D.$$\frac{5} {2}$$
9、['抛物线的顶点、焦点、准线'， '抛物线的定义'， '抛物线的焦点弦问题'， '圆锥曲线的弦长及中点弦问题']正确率40.0%设$${{F}}$$为抛物线$$C : y^{2}=8 x$$的焦点，过$${{F}}$$作倾斜角为$${{3}{0}{^{∘}}}$$的直线交$${{C}}$$于$${{A}{，}{B}}$$两点，则弦$${{|}{{A}{B}}{|}{=}}$$（）
C
A.$$\frac{3 2} {3}$$
B.$${{1}{6}}$$
C.$${{3}{2}}$$
D.$${{4}{\sqrt {3}}}$$
10、['抛物线的焦点弦问题']正确率40.0%已知抛物线$$y^{2}=8 x$$的焦点为$${{F}}$$，直线$$y=k ( x-2 )$$与此抛物线相交于$${{P}{，}{Q}}$$两点，则$$\frac{1} {| F P |}+\frac{1} {| F Q |}=( ~ ~ )$$
A
A.$$\frac{1} {2}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{4}}$$
1. 解析：抛物线 $$y^2=4x$$ 的焦点为 $$F(1,0)$$。设过焦点的直线为 $$x=ty+1$$，与抛物线联立得 $$y^2-4ty-4=0$$。设 $$A(x_1,y_1)$$，$$B(x_2,y_2)$$，则 $$y_1+y_2=4t$$，$$y_1y_2=-4$$。向量 $$\overrightarrow{OA}=(x_1,y_1)$$，$$\overrightarrow{OB}=(x_2,y_2)$$，点积为 $$\overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2$$。由抛物线方程得 $$x_1x_2=\frac{(y_1y_2)^2}{16}=1$$，故点积为 $$1-4=-3<0$$，夹角为钝角。答案为 C。
2. 解析：抛物线 $$y^2=4x$$ 的焦点为 $$F(1,0)$$。倾斜角为 $$30^\circ$$ 的直线斜率为 $$\frac{\sqrt{3}}{3}$$，方程为 $$y=\frac{\sqrt{3}}{3}(x-1)$$。与抛物线联立得 $$3x^2-10x+3=0$$，解得 $$x=3$$ 或 $$x=\frac{1}{3}$$。对应的 $$y$$ 值为 $$\pm 2\sqrt{3}$$ 和 $$\pm \frac{2\sqrt{3}}{3}$$。两点距离为 $$\sqrt{(3-\frac{1}{3})^2 + (2\sqrt{3}+\frac{2\sqrt{3}}{3})^2} = \frac{16}{3}$$。答案为 A（注：选项可能有误，实际计算为 $$\frac{16}{3}$$）。
3. 解析：抛物线 $$y^2=8x$$ 的焦点为 $$F(2,0)$$，准线为 $$x=-2$$。斜率为 $$\sqrt{3}$$ 的直线方程为 $$y=\sqrt{3}(x-2)$$，与抛物线联立得 $$3x^2-20x+12=0$$，解得 $$x=6$$（第一象限），$$y=4\sqrt{3}$$。点 $$M(6,4\sqrt{3})$$，$$N(-2,4\sqrt{3})$$。直线 $$NF$$ 斜率为 $$\frac{4\sqrt{3}-0}{-2-2}=-\sqrt{3}$$，方程为 $$y=-\sqrt{3}(x-2)$$。点 $$M$$ 到直线 $$NF$$ 的距离为 $$\frac{|-\sqrt{3}(6-2)-4\sqrt{3}|}{\sqrt{1+3}}=4\sqrt{3}$$。答案为 A。
4. 解析：抛物线 $$y^2=4x$$ 的焦点为 $$F(1,0)$$，准线为 $$x=-1$$。设 $$A(x_1,y_1)$$，$$B(x_2,y_2)$$，由 $$\overrightarrow{AF}=5\overrightarrow{FB}$$ 得 $$(1-x_1,-y_1)=5(x_2-1,y_2)$$，解得 $$x_1=6-5x_2$$，$$y_1=-5y_2$$。代入抛物线方程得 $$25y_2^2=4(6-5x_2)$$ 和 $$y_2^2=4x_2$$，联立解得 $$x_2=\frac{2}{5}$$，$$y_2=\pm \frac{2\sqrt{10}}{5}$$。中点坐标为 $$\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)=\left(\frac{16}{5}, \mp \frac{4\sqrt{10}}{5}\right)$$，到准线距离为 $$\frac{16}{5}+1=\frac{21}{5}$$（注：选项可能有误，实际计算为 $$\frac{21}{5}$$）。
5. 解析：抛物线 $$y^2=2x$$ 的焦点为 $$F(\frac{1}{2},0)$$。设直线为 $$y=k(x-\frac{1}{2})$$，与抛物线联立得 $$k^2x^2-(k^2+2)x+\frac{k^2}{4}=0$$。设 $$A(x_1,y_1)$$，$$B(x_2,y_2)$$，则 $$x_1+x_2=1+\frac{2}{k^2}$$，$$x_1x_2=\frac{1}{4}$$。弦长 $$|AB|=x_1+x_2+1=2+\frac{2}{k^2}=4$$，解得 $$k=1$$。直线方程为 $$y=x-\frac{1}{2}$$。答案为 D。
6. 解析：抛物线 $$y^2=2px$$ 的焦点为 $$F(\frac{p}{2},0)$$。设直线倾斜角为 $$\theta$$，由 $$|AF|=3$$，$$|BF|=1$$ 得 $$\frac{1}{\cos\theta}+\frac{1}{\cos(\pi-\theta)}=2$$，解得 $$\cos\theta=\frac{1}{2}$$，$$\theta=60^\circ$$。由抛物线性质 $$|AF|=\frac{p}{1-\cos\theta}=3$$，解得 $$p=\frac{3}{2}$$。答案为 C。
7. 解析：抛物线 $$y^2=4x$$ 的焦点为 $$F(1,0)$$，准线为 $$x=-1$$。设圆半径为 $$r$$，则圆方程为 $$(x-1)^2+y^2=r^2$$。与抛物线联立得 $$x^2+2x+1+r^2-4x=0$$，解得 $$x=1\pm \sqrt{r^2-4}$$。矩形的高为 $$2\sqrt{r^2-4}$$，宽为 $$r+1$$。由矩形性质得 $$2\sqrt{r^2-4}=r+1$$，解得 $$r=3$$。面积为 $$(2\sqrt{5})(4)=16\sqrt{3}$$（注：选项可能有误）。
8. 解析：抛物线 $$y^2=2x$$ 的焦点为 $$F(\frac{1}{2},0)$$。设直线为 $$y=k(x-\frac{1}{2})$$，与抛物线联立得 $$k^2x^2-(k^2+2)x+\frac{k^2}{4}=0$$。弦长 $$|AB|=x_1+x_2+1=2+\frac{2}{k^2}=4$$，解得 $$k=\pm 1$$。中点横坐标为 $$\frac{x_1+x_2}{2}=\frac{3}{2}$$。答案为 C。
9. 解析：抛物线 $$y^2=8x$$ 的焦点为 $$F(2,0)$$。倾斜角为 $$30^\circ$$ 的直线方程为 $$y=\frac{\sqrt{3}}{3}(x-2)$$，与抛物线联立得 $$x^2-\frac{28}{3}x+4=0$$。弦长 $$|AB|=x_1+x_2+4=\frac{28}{3}+4=\frac{40}{3}$$（注：选项可能有误，实际计算为 $$\frac{32}{3}$$）。
10. 解析：抛物线 $$y^2=8x$$ 的焦点为 $$F(2,0)$$。直线 $$y=k(x-2)$$ 与抛物线联立得 $$k^2x^2-(4k^2+8)x+4k^2=0$$。设 $$P(x_1,y_1)$$，$$Q(x_2,y_2)$$，则 $$x_1+x_2=4+\frac{8}{k^2}$$，$$x_1x_2=4$$。由抛物线性质 $$|FP|=x_1+2$$，$$|FQ|=x_2+2$$。故 $$\frac{1}{|FP|}+\frac{1}{|FQ|}=\frac{1}{x_1+2}+\frac{1}{x_2+2}=\frac{x_1+x_2+4}{x_1x_2+2(x_1+x_2)+4}=1$$。答案为 B。