正确率40.0%给出关于双曲线的三个命题:
$${①}$$双曲线$$\frac{y^{2}} {9}-\frac{x^{2}} {4}=1$$的渐近线方程为$$y=\pm\frac{2} {3} x$$;
$${②}$$若点$$( 2, \ 3 )$$在焦距为$${{4}}$$的双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1$$上,则此双曲线的离心率为$${{2}}$$;
$${③}$$若点$${{F}{,}{B}}$$分别是双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1$$的一个焦点和虚轴的一个端点,则线段$${{F}{B}}$$的中点一定不在此双曲线的渐近线上.
其中正确的命题个数是()
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
2、['点与圆的位置关系', '圆的定义与标准方程', '三角形的面积(公式)', '双曲线的顶点、长轴、短轴、焦点、焦距', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知双曲线$$C_{:} \, \, x^{2}-y^{2}=2$$的左右焦点$$F_{1}, ~ F_{2}, ~ O$$为坐标原点,点$${{P}}$$在双曲线$${{C}}$$上,且$$| O P |=2$$,则$$S_{\triangle P F_{1} F_{2}}=\c n$$)
C
A.$${{4}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${{2}}$$
D.$${\sqrt {2}}$$
3、['正弦定理及其应用', '圆锥曲线中求轨迹方程', '双曲线的定义', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知锐角$${{Δ}{A}{B}{C}}$$中,角$$A, B, C$$所对边分别为$$a, b, c$$,若$$a=4, \, \, \, \operatorname{s i n} B-\operatorname{s i n} C=\frac{1} {2} \operatorname{s i n} A$$,则$${{B}{C}}$$边上中线长的取值范围为
B
A.$$( 1, \, 3 )$$
B.$$( 2, \, \sqrt{1 3} )$$
C.$$( 2, \, \sqrt{1 0} )$$
D.$$( 1, \, \sqrt{7} )$$
4、['向量坐标与向量的数量积', '双曲线的顶点、长轴、短轴、焦点、焦距', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知双曲线$$\frac{x^{2}} {2}-y^{2}=1$$的左$${、}$$右焦点分别为$${{F}_{1}{,}{{F}_{2}}}$$,点$$M ( x_{0}, y_{0} )$$在双曲线上,且满足$$\overrightarrow{M F_{1}} \cdot\overrightarrow{M F_{2}} \leqslant0$$,则$${{y}_{0}}$$取值范围是$${{(}{)}}$$
A
A.$$[-\frac{\sqrt{3}} {3}, \frac{\sqrt{3}} {3} ]$$
B.$$[-\frac{\sqrt{3}} {6}, \frac{\sqrt{3}} {6} ]$$
C.$$[-\frac{2 \sqrt{3}} {3}, \frac{2 \sqrt{3}} {3} ]$$
D.$$[-\frac{3 \sqrt{2}} {2}, \frac{3 \sqrt{2}} {2} ]$$
5、['双曲线的离心率', '双曲线的渐近线', '直线系方程', '直线与双曲线的综合应用', '双曲线的顶点、长轴、短轴、焦点、焦距', '双曲线的对称性', '直线的斜率', '双曲线上点的横坐标与纵坐标的范围', '直线与双曲线的交点个数']正确率40.0%设双曲线$$C_{\colon} \, \, \frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 \, \, ( \mathrm{~} a > 0, \mathrm{~} b > 0 )$$的左$${、}$$右焦点分别为$${{F}_{1}{,}{{F}_{2}}}$$,过点$${{F}_{1}}$$且斜率为$$\frac{1} {3}$$的直线与双曲线的两渐近线分别交于点$${{A}{,}{B}}$$,并且$$| F_{2} \, A |=| F_{2} B |$$,则双曲线的离心率为()
A
A.$$\frac{\sqrt5} {2}$$
B.$${\sqrt {2}}$$
C.$${{2}}$$
D.$${\sqrt {5}}$$
6、['利用基本不等式求最值', '双曲线的标准方程', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知方程$$m x^{2}+~ ( m-3 ) ~ y^{2}=1$$表示双曲线,则此双曲线的焦距的最小值为()
A
A.$$\frac{4 \sqrt{3}} {3}$$
B.$${\sqrt {6}}$$
C.$${{3}}$$
D.$${{2}{\sqrt {3}}}$$
7、['双曲线的离心率', '直线与双曲线的综合应用', '双曲线的顶点、长轴、短轴、焦点、焦距', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知点$${{F}_{1}{,}{{F}_{2}}}$$分别是双曲线$$C : \frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0, b > 0 )$$的左右两焦点,过点$${{F}_{1}}$$的直线$${{l}}$$与双曲线的左右两支分别交于$${{P}{,}{Q}}$$两点,若$${{Δ}{P}{Q}{{F}_{2}}}$$是以$${{∠}{P}{Q}{{F}_{2}}}$$为顶角的等腰三角形,其中$$\angle P Q F_{2} \in[ \frac{\pi} {3}, \pi),$$则双曲线离心率$${{e}}$$的取值范围为
A
A.$$[ \sqrt{7}, 3 )$$
B.$$[ 1, \sqrt{7} )$$
C.$$[ \sqrt{5}, 3 )$$
D.$$[ \sqrt{5}, \sqrt{7} )$$
8、['双曲线的离心率', '两点间的距离', '双曲线的顶点、长轴、短轴、焦点、焦距', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知点$${{F}_{1}{,}{{F}_{2}}}$$分别为双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 \, ( a > 0, b > 0 )$$的左$${、}$$右两个焦点,点$${{P}}$$是双曲线右支上一点,若$${{P}}$$点的横坐标$$x_{0}=\frac{4} {3} a$$时,有$$F_{1} P \bot F_{2} P$$,则该双曲线的离心率$${{e}}$$为$${{(}{)}}$$
A
A.$${\frac{3} {2}} \sqrt{2}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$${{2}}$$
D.$$\frac{9} {2}$$
9、['双曲线的离心率', '双曲线的对称性', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知双曲线$$C_{\colon} \, \, \frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0, b > 0 )$$的左右焦点分别为$${{F}_{1}{,}{{F}_{2}}}$$,双曲线$${{C}}$$与圆$$x^{2}+y^{2}=a^{2}+b^{2}$$在第一象限的交点为$$P, \, \, \bot P F_{1} F_{2}$$的角平分线与$${{P}{{F}_{2}}}$$交于点$${{Q}}$$,若$$4 \left| P Q \right|=3 \left| F_{2} Q \right|$$,则双曲线$${{C}}$$的离心率为$${{(}{)}}$$
A
A.$${{6}{+}{2}{\sqrt {7}}}$$
B.$${{3}{+}{\sqrt {7}}}$$
C.$${{6}{−}{2}{\sqrt {7}}}$$
D.$${{4}{−}{\sqrt {7}}}$$
10、['双曲线的离心率', '双曲线的其他性质', '双曲线上点的横坐标与纵坐标的范围']正确率40.0%已知双曲线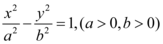 的左,右焦点分别为
的左,右焦点分别为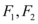 ,点$${{P}}$$
,点$${{P}}$$
B
A.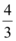
B.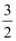
C.
D.
.jpg)