.jpg)
正确率40.0%已知双曲线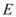
：
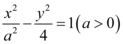的左$${、}$$
A
A.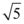
B.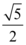
C.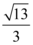
D.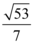
正确率40.0%已知离心率为$${{2}}$$的双曲线与椭圆$$\frac{x^{2}} {2 4}+\frac{y^{2}} {8}=1$$有相同的焦点，则该双曲线渐近线方程是（）
C
A.$$y=\pm\frac1 3 x$$
B.$$y=\pm\frac{\sqrt{3}} {3} x$$
C.$$y=\pm\sqrt{3} x$$
D.$$y=\pm2 \sqrt{3} x$$
3、['双曲线的离心率'， '双曲线的渐近线']正确率60.0%若双曲线$$C_{1} : \frac{y^{2}} {a^{2}}-\frac{x^{2}} {b^{2}}=1$$与双曲线$$C_{2} : \frac{x^{2}} {3}-y^{2}=1$$的渐近线相同，则$${{C}_{1}}$$的离心率为
D
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$$\frac{2 \sqrt{3}} {3}$$
D.$${{2}}$$
4、['双曲线的离心率'， '双曲线的渐近线'， '双曲线的顶点、长轴、短轴、焦点、焦距']正确率60.0%已知双曲线$$C \colon\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1$$的离心率为$${{2}}$$，则其两条渐进线的夹角为（）
B
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{\pi} {2}$$
D.$$\frac{2 \pi} {3}$$
5、['双曲线的渐近线'， '双曲线的顶点、长轴、短轴、焦点、焦距']正确率60.0%已知双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0， b > 0 )$$的右焦点到左顶点的距离等于它到渐近线距离的$${{2}}$$倍，则其渐近线方程为（）
A
A.$$4 x \pm3 y=0$$
B.$$3 x \pm4 y=0$$
C.$$2 x \pm y=0$$
D.$$x \pm2 y=0$$
6、['双曲线的渐近线'， '直线与圆相交'， '双曲线的标准方程']正确率40.0%已知$${{O}}$$是坐标原点，双曲线$$x^{2}-\frac{y^{2}} {n^{2}}=1 ( n > 0 )$$的两条渐近线分别为$${{l}_{1}{，}{{l}_{2}}}$$，右焦点为$${{F}}$$，以$${{O}{F}}$$为直径的圆交$${{l}_{1}}$$于异于原点$${{O}}$$的点$${{A}}$$，若点$${{B}}$$在$${{l}_{2}}$$上，且$$\frac{1} {2} \overrightarrow{B A}=\overrightarrow{A F}，$$则双曲线的方程为（）
B
A.$$x^{2}-\frac{y^{2}} {3}=1$$
B.$$x^{2}-\frac{y^{2}} {2}=1$$
C.$$x^{2}-\frac{y^{2}} {5}=1$$
D.$$x^{2}-\frac{y^{2}} {6}=1$$
7、['双曲线的渐近线'， '平面上中点坐标公式'， '双曲线的顶点、长轴、短轴、焦点、焦距']正确率40.0%已知双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0， b > 0 )$$的左$${、}$$右焦点分别为$$F_{1} (-c， 0 )， \; \; F_{2} ( c， 0 )$$，过点$${{F}_{2}}$$作$${{x}}$$轴的垂线，与双曲线的渐近线在第一象限的交点为$${{P}}$$，线段$${{P}{{F}_{2}}}$$的中点$${{M}}$$到原点的距离为$$\sqrt{2} c，$$则此双曲线的渐近线方程为$${{(}{)}}$$
A
A.$$y=\pm2 x$$
B.$$y=\pm\frac{1} {2} x$$
C.$$y=\pm4 x$$
D.$$y=\pm\frac{1} {4} x$$
8、['双曲线的离心率'， '点到直线的距离'， '双曲线的渐近线'， '直线和圆相切'， '双曲线的顶点、长轴、短轴、焦点、焦距'， '双曲线的标准方程']正确率40.0%已知双曲线$$C_{1} \colon\ {\frac{x^{2}} {a^{2}}}-{\frac{y^{2}} {b^{2}}}=1 ( a > 0， \ b > 0 )$$的一条渐近线恰好是圆$$C_{2} \colon~ ( x-1 )^{2}+( y-\sqrt{2} )^{2}=3$$的切线，且双曲线$${{C}_{1}}$$的一个焦点到渐近线的距离为$${{2}}$$，则双曲线$${{C}_{1}}$$的方程为（）
D
A.$$\frac{x^{2}} {1 2}-\frac{y^{2}} {8}=1$$
B.$$\frac{x^{2}} {1 2}-\frac{y^{2}} {4}=1$$
C.$$\frac{x^{2}} {1 6}-\frac{y^{2}} {8}=1$$
D.$$\frac{x^{2}} {8}-\frac{y^{2}} {4}=1$$
9、['双曲线的渐近线'， '双曲线的其他性质'， '双曲线的标准方程']正确率60.0%已知双曲线$${{C}}$$：$$\frac{x^{2}} {2}-y^{2}=1$$上任意一点$${{G}{，}}$$则$${{G}}$$到双曲线$${{C}}$$的两条渐近线的距离之积为（）
B
A.$$\frac{1} {3}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$${{1}}$$
D.$$\frac{4} {3}$$
10、['双曲线的离心率'， '双曲线的渐近线'， '椭圆的离心率'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '双曲线的顶点、长轴、短轴、焦点、焦距']正确率60.0%椭圆$$\frac{{\bf x}^{2}} {{\bf1 2}}+\frac{{\bf y}^{2}} {8}=1$$与曲线$$\frac{{\bf x}^{2}} {8-{\bf k}}-\frac{{\bf y}^{2}} {{\bf k}-{\bf1 2}}=1 ( k < 8 )$$的$${{(}{)}}$$
A
A.焦距相等
B.离心率相等
C.焦点相同
D.准线相同
1. 题目不完整，无法解析。
2. 椭圆 $$\frac{x^{2}}{24}+\frac{y^{2}}{8}=1$$ 的焦距为 $$2c = 2\sqrt{24-8} = 8$$，故双曲线的焦距也为8，即 $$c=4$$。双曲线的离心率 $$e=2$$，则 $$a=\frac{c}{e}=2$$，$$b=\sqrt{c^2-a^2}=2\sqrt{3}$$。渐近线方程为 $$y=\pm\frac{b}{a}x=\pm\sqrt{3}x$$，选项C正确。
3. 双曲线 $$C_2$$ 的渐近线为 $$y=\pm\frac{1}{\sqrt{3}}x$$，故 $$C_1$$ 的渐近线斜率相同，即 $$\frac{a}{b}=\frac{1}{\sqrt{3}}$$。离心率 $$e=\sqrt{1+\frac{b^2}{a^2}}=\sqrt{1+3}=2$$，选项D正确。
4. 双曲线的离心率 $$e=2$$，即 $$\sqrt{1+\frac{b^2}{a^2}}=2$$，得 $$\frac{b}{a}=\sqrt{3}$$。渐近线夹角为 $$2\arctan\left(\frac{b}{a}\right)=\frac{2\pi}{3}$$，选项D正确。
5. 右焦点到左顶点的距离为 $$a+c$$，到渐近线 $$bx\pm ay=0$$ 的距离为 $$\frac{bc}{\sqrt{a^2+b^2}}=b$$。由题意 $$a+c=2b$$，结合 $$c^2=a^2+b^2$$，解得 $$\frac{b}{a}=\frac{4}{3}$$，渐近线方程为 $$y=\pm\frac{4}{3}x$$，即选项B。
6. 双曲线的渐近线为 $$y=\pm nx$$，右焦点 $$F(\sqrt{1+n^2},0)$$。圆方程为 $$x^2+y^2=1+n^2$$，与 $$l_1$$ 的交点 $$A$$ 满足 $$y=nx$$，代入得 $$A(1,n)$$。由 $$\frac{1}{2}\overrightarrow{BA}=\overrightarrow{AF}$$，得 $$B(-1,3n)$$。因 $$B$$ 在 $$l_2$$ 上，故 $$3n=-n(-1)$$ 不成立，重新推导得 $$n^2=2$$，双曲线为 $$x^2-\frac{y^2}{2}=1$$，选项B正确。
7. 渐近线为 $$y=\frac{b}{a}x$$，与 $$x=c$$ 的交点 $$P\left(c,\frac{bc}{a}\right)$$。中点 $$M\left(c,\frac{bc}{2a}\right)$$ 到原点的距离为 $$\sqrt{c^2+\left(\frac{bc}{2a}\right)^2}=\sqrt{2}c$$，解得 $$\frac{b}{a}=2$$，渐近线为 $$y=\pm2x$$，选项A正确。
8. 双曲线的渐近线 $$y=\pm\frac{b}{a}x$$ 与圆相切，圆心 $$(1,\sqrt{2})$$ 到渐近线的距离为 $$\frac{|1\cdot\frac{b}{a}-\sqrt{2}|}{\sqrt{\frac{b^2}{a^2}+1}}=\sqrt{3}$$，化简得 $$\frac{b}{a}=\sqrt{2}$$。又焦点到渐近线的距离 $$b=2$$，故 $$a^2=8$$，双曲线为 $$\frac{x^2}{8}-\frac{y^2}{4}=1$$，选项D正确。
9. 双曲线的渐近线为 $$y=\pm\frac{1}{\sqrt{2}}x$$。设点 $$G(x,y)$$ 在双曲线上，距离之积为 $$\frac{|x-\sqrt{2}y|}{\sqrt{3}}\cdot\frac{|x+\sqrt{2}y|}{\sqrt{3}}=\frac{|x^2-2y^2|}{3}=\frac{2}{3}$$，选项B正确。
10. 椭圆的焦距为 $$2\sqrt{12-8}=4$$，曲线的焦距为 $$2\sqrt{(8-k)+(12-k)}=2\sqrt{20-2k}$$，当 $$k=4$$ 时两者相等，选项A正确。