正确率60.0%已知 $${{F}}$$$${}_{1} (-3, 0 )$$, $${{F}}$$$${}_{2} ( 3, 0 )$$是椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ($$ $${{a}}$$$${{>}}$$ $${{b}}$$$${{>}{0}{)}}$$两个焦点, $${{P}}$$在椭圆上,$${{∠}}$$ $${{F}}$$$${_{1}}$$ $${{P}{F}}$$$${_{2}{=}}$$ $${{α}}$$,且当 $${{α}}$$$$= \frac{2 \pi} {3}$$时,$${{△}}$$ $${{F}}$$$${_{1}}$$ $${{P}{F}}$$$${_{2}}$$的面积最大,则椭圆的标准方程为$${{(}{)}}$$
A
A.$$\frac{x^{2}} {1 2}+\frac{y^{2}} {3}=1$$
B.$$\frac{x^{2}} {1 4}+\frac{y^{2}} {5}=1$$
C.$$\frac{x^{2}} {1 5}+\frac{y^{2}} {6}=1$$
D.$$\frac{x^{2}} {1 6}+\frac{y^{2}} {7}=1$$
2、['椭圆的离心率', '椭圆的对称性', '椭圆的顶点、长轴、短轴、焦点、焦距', '三角形的面积(公式)', '直线和圆相切']正确率40.0%已知椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左$${、}$$右焦点分别为$${{F}_{1}{,}{{F}_{2}}}$$,过$${{F}_{1}}$$作垂直于$${{x}}$$轴的直线交椭圆于$${{A}{,}{B}}$$两点,若$${{△}{A}{B}{{F}_{2}}}$$的内切圆半径为$$\frac{3} {8} a,$$则椭圆的离心率$${{e}{=}{(}{)}}$$
$${}$$
B
A.$$\frac{1} {2}$$
B.$$\frac{1} {2}$$或$$\frac{\sqrt{1 3}-1} {4}$$
C.$$\frac{\sqrt{5}-1} {2}$$
D.$$\frac{\sqrt{1 3}-1} {4}$$
3、['基本不等式:(√ab)≤(a+b)/2,当且仅当a=b时等号成立', '椭圆的对称性']正确率60.0%椭圆$$\frac{x^{2}} {4}+\frac{y^{2}} {2}=1$$的内接矩形面积的最大值为 ()
A
A.$${{4}{\sqrt {2}}}$$
B.$${\sqrt {2}}$$
C.$${{4}}$$
D.$${{2}}$$
4、['椭圆的离心率', '椭圆的对称性', '椭圆的顶点、长轴、短轴、焦点、焦距', '椭圆的定义']正确率60.0%设椭圆$$C_{\colon} \ \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左、右焦点分别为$$F_{1}, F_{2},$$过$${{F}_{2}}$$的直线与$${{C}}$$交于$${{A}{,}{B}}$$两点,若$${{△}{A}{B}{{F}_{1}}}$$为等边三角形,则$${{C}}$$的离心率为()
A
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{\sqrt2} 3$$
D.$$\frac{1} {2}$$
5、['椭圆的离心率', '椭圆的对称性', '椭圆的顶点、长轴、短轴、焦点、焦距']正确率60.0%已知点$${{P}}$$为椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 \ ( \mathrm{~} a > b > 0 )$$上一点,$${{F}_{1}{,}{{F}_{2}}}$$分别为其左$${、}$$右焦点,且$$P F_{1} \perp P F_{2}, \, \, \, \angle P F_{1} F_{2}=6 0^{\circ}$$. 则$${{e}{=}{(}}$$)
D
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{\sqrt3-1} {2}$$
D.$$\sqrt3-1$$
6、['平面解析几何的新定义问题', '椭圆的对称性', '椭圆的顶点、长轴、短轴、焦点、焦距']正确率40.0%我们把由半椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1$$$$( x \geqslant0 )$$与半椭圆$$\frac{y^{2}} {b^{2}}+\frac{x^{2}} {c^{2}}=1$$$$( x \leqslant0 )$$合成的曲线称作$${{“}}$$果圆$${{”}}$$,其中$$a^{2}=b^{2}+c^{2}, \, \, \, a > 0, \, \, \, b > c > 0$$.如图,设点$$F_{0}, ~ F_{1}, ~ F_{2}$$是相应椭圆的焦点,$${{A}_{1}{,}{{A}_{2}}}$$和$${{B}_{1}{,}{{B}_{2}}}$$是$${{“}}$$果圆$${{”}}$$与$${{x}{,}{y}}$$轴的交点,若$${{Δ}{{F}_{0}}{{F}_{1}}{{F}_{2}}}$$是边长为$${{1}}$$的等边三角形,则$$a^{2}+b^{2}=($$$${{)}}$$.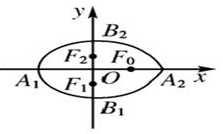
B
A.$${{3}}$$
B.$$\frac{1 1} {4}$$
C.$$\frac{5} {2}$$
D.$$\frac{9} {4}$$
7、['椭圆的离心率', '椭圆的对称性', '椭圆的标准方程', '椭圆的顶点、长轴、短轴、焦点、焦距', '直线与椭圆的综合应用']正确率60.0%已知椭圆$$C : \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左$${、}$$右焦点分别为$${{F}_{1}{,}{{F}_{2}}}$$,离心率为$$\frac{1} {2},$$过$${{F}_{2}}$$的直线与椭圆$${{C}}$$交于$${{A}{,}{B}}$$两点.若$${{△}{{F}_{1}}{A}{B}}$$的周长为$${{8}}$$,则椭圆方程为$${{(}{)}}$$
A
A.$$\frac{x^{2}} {4}+\frac{y^{2}} {3}=1$$
B.$$\frac{x^{2}} {1 6}+\frac{y^{2}} {1 2}=1$$
C.$$\frac{x^{2}} {2}+y^{2}=1$$
D.$$\frac{x^{2}} {4}+\frac{y^{2}} {2}=1$$
8、['椭圆的离心率', '椭圆的对称性']正确率40.0%已知$${{F}}$$是椭圆$$E : \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左焦点,经过原点的直线$${{l}}$$与椭圆$${{E}}$$交于$${{P}{,}{Q}}$$两点,若,且$$\angle P F Q \!=\! 1 2 0^{\circ} \,,$$则椭圆$${{E}}$$的离心率为
C
A.$$\frac{1} {3}$$
B.$$\frac{1} {2}$$
C.$$\frac{\sqrt{3}} {3}$$
D.$$\frac{\sqrt2} {2}$$
9、['圆的定义与标准方程', '椭圆的对称性', '椭圆的标准方程', '椭圆的顶点、长轴、短轴、焦点、焦距', '椭圆的其他性质']正确率40.0%已知椭圆$$C : ~ \frac{x^{2}} {m}+y^{2}=1 ( m > 1 )$$的左,右焦点分别为$${{F}_{1}{,}{{F}_{2}}}$$,左,右顶点为$${{M}{,}{N}}$$,以线段$${{F}_{1}{{F}_{2}}}$$为直径的圆与椭圆$${{C}}$$有$${{4}}$$个公共点$$P_{i} ( i=1, 2, 3, 4 )$$,则$$\frac{\sum_{i=1}^{4} ( k_{p_{i} M} \cdot k_{P_{i} N} )} {m}$$的取值范围是()
B
A.$$(-\frac{4} {2 5}, 0 )$$
B.$$(-1, 0 )$$
C.$$( 0, \frac{4} {2 5} )$$
D.$$( 0, 1 )$$
10、['椭圆的离心率', '圆的一般方程', '椭圆的对称性']正确率40.0%椭圆$$x^{2}+\frac{y^{2}} {b^{2}}=1 \, ( 0 < b < 1 )$$的左焦点为$${{F}}$$,上顶点为$${{A}}$$,右顶点为$${{B}}$$,若$${{Δ}{F}{A}{B}}$$的外接圆圆心$$P \, ( m, n )$$在直线$${{y}{=}{−}{x}}$$的左下方,则该椭圆离心率的取值范围为()
A
A.$$\left( \frac{\sqrt{2}} {2}, 1 \right)$$
B.$$\left( \frac{1} {2}, 1 \right)$$
C.$$\left( 0, \frac{\sqrt{2}} {2} \right)$$
D.$$\left( 0, \frac{1} {2} \right)$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)