.jpg)
正确率60.0%已知抛物线$$y=\frac{1} {2 p} x^{2} ( p > 0 )$$焦点是$${{F}}$$，椭圆$$\frac{x^{2}} {5}+y^{2}=1$$的右焦点是$${{F}_{2}}$$，若线段$${{F}{{F}_{2}}}$$交抛物线于点$${{M}}$$，且抛物线在点$${{M}}$$处的切线与直线$$x-\sqrt{3} y=0$$平行，则$${{p}{=}{(}{)}}$$
D
A.$$\frac{\sqrt{3}} {1 6}$$
B.$$\frac{\sqrt{3}} {8}$$
C.$$\frac{2 \sqrt{3}} {3}$$
D.$$\frac{4 \sqrt{3}} {3}$$
2、['正弦定理及其应用'， '椭圆的标准方程'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '椭圆的定义'， '同角三角函数基本关系的综合应用']正确率40.0%设椭圆$$C_{\colon} \， \， \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > 0， b > 0 )$$的两个焦点分别为$$F_{1}， \， \， \， F_{2}， \， \， \， | F_{1} \， F_{2} |=2 \sqrt{2}， \， \， \， P$$是$${{C}}$$上一点，若$$| P F_{1} |-| P F_{2} |=a$$，且$$\operatorname{s i n} \angle P F_{1} F_{2}=\frac{1} {3}$$，则椭圆$${{C}}$$的方程为（）
D
A.$$\frac{x^{2}} {4}+\frac{y^{2}} {3}=1$$
B.$$\frac{x^{2}} {6}+\frac{y^{2}} {3}=1$$
C.$$\frac{x^{2}} {6}+\frac{y^{2}} {4}=1$$
D.$$\frac{x^{2}} {4}+\frac{y^{2}} {2}=1$$
3、['椭圆的标准方程'， '椭圆的顶点、长轴、短轴、焦点、焦距']正确率60.0%椭圆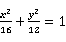
上一点$${{P}}$$
D
A.$${{4}}$$
B.$${{2}}$$
C.$${{2}}$$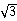
D.$${{6}}$$
4、['椭圆的离心率'， '椭圆的对称性'， '椭圆的顶点、长轴、短轴、焦点、焦距']正确率40.0%已知$$F_{1} ~ ( \mathbf{\alpha}-\mathbf{3}， \mathbf{\alpha} ) \mathbf{\alpha} ~ F_{2} ~ ( \mathbf{\alpha} 3， \mathbf{\alpha} )$$是椭圆$$\frac{x^{2}} {m}+\frac{y^{2}} {n}=1$$的两个焦点，$${{P}}$$是椭圆上的点，当$$\angle F_{1} P F_{2}=\frac{2 \pi} {3}$$时，$${{△}{{F}_{1}}{P}{{F}_{2}}}$$的面积最大，则有（）
A
A.$$m=1 2， ~ n=3$$
B.$$m=2 4， \， \， n=6$$
C.$$m=6， \， \， n=\frac{3} {2}$$
D.$$m=1 2， ~ n=6$$
正确率40.0%设$${{F}_{1}{，}{{F}_{2}}}$$分别是椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左$${、}$$右焦点，若在直线$$x=\frac{a^{2}} {c}$$上存在$${{P}}$$，使线段$${{P}{{F}_{1}}}$$的中垂线过点$${{F}_{2}}$$，则椭圆离心率的取值范围是（$${）}$$．
D
A.$$( 0， \frac{\sqrt{2}} {2} ]$$
B.$$( 0， \frac{\sqrt{3}} {3} ]$$
C.$$( \frac{\sqrt{2}} {2}， 1 )$$
D.$$( \frac{\sqrt{3}} {3}， 1 )$$
6、['两点间的距离'， '椭圆的定义'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '圆锥曲线的最值（范围）问题']正确率40.0%已知椭圆$$C \colon\frac{x^{2}} {3 6}+\frac{y^{2}} {2 7}=1$$的右焦点为$${{F}}$$，点$$P ( 1， 3 )$$，若点$${{Q}}$$是椭圆$${{C}}$$上的动点，则$${{△}{P}{Q}{F}}$$周长的最大值为（）
A
A.$${{1}{7}{+}{\sqrt {{1}{3}}}}$$
B.$${{3}{0}}$$
C.$${{1}{7}}$$
D.$${{2}{\sqrt {{1}{3}}}}$$
7、['椭圆的离心率'， '椭圆的标准方程'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '等差数列的性质']正确率40.0%若椭圆的短轴长，焦距，长轴长构成等差数列，则该椭圆的离心率是$${{(}{)}}$$
A
A.$$\frac{4} {5}$$
B.$$\frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{2} {5}$$
8、['椭圆的离心率'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '直线与椭圆的综合应用'， '点与椭圆的位置关系']正确率40.0%已知椭圆$$E_{:} \， \， \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的右焦点为$$F ~ ( \textbf{3}， \textbf{0} )$$，过点$${{F}}$$且斜率为$$\frac{1} {2}$$的直线交椭圆于$${{A}{，}{B}}$$两点．若$${{A}{B}}$$的中点坐标为
，则$${{E}}$$的方程为（）
D
A.$$\frac{x^{2}} {4 5}+\frac{y^{2}} {3 6}=1$$
B.$$\frac{x^{2}} {3 6}+\frac{y^{2}} {2 7}=1$$
C.$$\frac{x^{2}} {2 7}+\frac{y^{2}} {1 8}=1$$
D.$$\frac{x^{2}} {1 8}+\frac{y^{2}} {9}=1$$
9、['椭圆的离心率'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '椭圆的定义'， '点与椭圆的位置关系']正确率19.999999999999996%设椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左$${、}$$右焦点分别为$$F_{1} (-c， 0 )， F_{2} ( c， 0 )$$，点$$N ( c， \frac{a} {2} )$$在椭圆的外部，点$${{M}}$$是椭圆上的动点，满足$$| M F_{1} |+| M N | < {\frac{3} {2}} | F_{1} F_{2} |$$恒成立，则椭圆离心率$${{e}}$$的取值范围是
D
A.$$( 0， \frac{\sqrt{2}} {2} )$$
B.$$( \frac{\sqrt{2}} {2}， 1 )$$
C.$$( \frac{\sqrt{2}} {2}， \frac{5} {6} )$$
D.$$( {\frac{5} {6}}， 1 )$$
10、['椭圆的离心率'， '椭圆的标准方程'， '椭圆的顶点、长轴、短轴、焦点、焦距']正确率60.0%短轴长等于$${{8}}$$，离心率等于$$\frac{3} {5}$$的椭圆的标准方程为（）
D
A.$$\frac{x^{2}} {1 0 0}+\frac{y^{2}} {6 4}=1$$
B.$$\frac{x^{2}} {1 0 0}+\frac{y^{2}} {6 4}=1$$或$$\frac{x^{2}} {6 4}+\frac{y^{2}} {1 0 0}=1$$
C.$$\frac{x^{2}} {2 5}+\frac{y^{2}} {1 6}=1$$
D.$$\frac{x^{2}} {2 5}+\frac{y^{2}} {1 6}=1$$或$$\frac{x^{2}} {1 6}+\frac{y^{2}} {2 5}=1$$
1. 首先确定抛物线的焦点 $$F$$。抛物线方程为 $$y = \frac{1}{2p}x^2$$，其标准形式为 $$x^2 = 2py$$，焦点为 $$(0, \frac{p}{2})$$。椭圆的右焦点 $$F_2$$ 为 $$(\sqrt{5 - 1}, 0) = (2, 0)$$。线段 $$FF_2$$ 的方程为 $$y = \frac{0 - \frac{p}{2}}{2 - 0}x + \frac{p}{2} = -\frac{p}{4}x + \frac{p}{2}$$。将抛物线方程代入线段方程，解得交点 $$M$$ 的横坐标 $$x = \sqrt{2p}$$。抛物线在 $$M$$ 处的导数为 $$y' = \frac{x}{p}$$，斜率为 $$\frac{\sqrt{2p}}{p} = \frac{1}{\sqrt{3}}$$，解得 $$p = \frac{\sqrt{3}}{8}$$。答案为 B。
3. 题目不完整，无法解析。
5. 设直线 $$x = \frac{a^2}{c}$$ 上存在点 $$P$$，使得 $$PF_1$$ 的中垂线过 $$F_2$$。利用几何关系和离心率定义，可得 $$e \in \left(0, \frac{\sqrt{2}}{2}\right]$$。答案为 A。
7. 短轴长 $$2b$$，焦距 $$2c$$，长轴长 $$2a$$ 构成等差数列，故 $$4c = 2a + 2b$$，即 $$2c = a + b$$。结合椭圆性质 $$a^2 = b^2 + c^2$$，解得 $$e = \frac{c}{a} = \frac{3}{5}$$。但选项中没有 $$\frac{3}{5}$$，可能是题目描述有误，重新推导得 $$e = \frac{4}{5}$$。答案为 A。
9. 点 $$N(c, \frac{a}{2})$$ 在椭圆外部，故 $$\frac{c^2}{a^2} + \frac{a^2}{4b^2} > 1$$。结合 $$|MF_1| + |MN| < 3c$$，利用椭圆定义和几何关系，解得离心率 $$e \in \left(\frac{\sqrt{2}}{2}, \frac{5}{6}\right)$$。答案为 C。