.jpg)
正确率40.0%设函数$$f ( x )=\operatorname{s i n} ( \omega x+\varphi) ( \omega> 0 )$$，己知集合$$A=\{( x_{0}， f ( x_{0} ) ) | x_{0} \uplus f ( x ) \nuplus\sharp\sharp\n\# \}，$$$$B=\{( x， y ) | \frac{x^{2}} {6}+\frac{y^{2}} {2} \leq1 \}$$，若存在实数$${{φ}{，}}$$使得集合$${{A}{∩}{B}}$$中恰好有$${{5}}$$个元素，则$${{ω}}$$的取值范围是（）
A
A.$$[ \frac{2 \sqrt{3}} {3} \pi， \frac{5 \sqrt{3}} {6} \pi)$$
B.$$[ \frac{2 \sqrt{3}} {3} \pi， \frac{3 \sqrt{3}} {4} \pi)$$
C.$$[ \frac{3 \sqrt{3}} {4} \pi， \frac{5 \sqrt{3}} {6} \pi)$$
D.$$[ \frac{3 \sqrt{3}} {4} \pi， \frac{1 1 \sqrt{3}} {1 2} \pi)$$
2、['椭圆的顶点、长轴、短轴、焦点、焦距'， '向量垂直'， '点与椭圆的位置关系']正确率60.0%已知椭圆$$\frac{x^{2}} {4}+y^{2}=1$$的焦点为$${{F}_{1}{，}{{F}_{2}}}$$，点$${{M}}$$在该椭圆上，且$$\overrightarrow{M F_{1}} \cdot\overrightarrow{M F_{2}}=0，$$则点$${{M}}$$到$${{x}}$$轴的距离为(
C
A.$$\frac{2 \sqrt{3}} {3}$$
B.$$\frac{2 \sqrt{6}} {3}$$
C.$$\frac{\sqrt{3}} {3}$$
D.$${\sqrt {3}}$$
3、['平面向量加法、减法的坐标运算'， '向量坐标与向量的数量积'， '点与椭圆的位置关系']正确率40.0%已知椭圆$$\frac{x^{2}} {4}+y^{2}=1$$的焦点分别是$${{F}_{1}{，}{{F}_{2}}}$$，点$${{M}}$$在该椭圆上，如果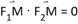
，那么点$${{M}}$$
B
A.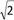
B.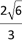
C.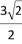
D.$${{1}}$$
4、['椭圆的离心率'， '椭圆的标准方程'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '椭圆的定义'， '点与椭圆的位置关系']正确率19.999999999999996%设椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 \， ( a > b > 0 )$$的左$${、}$$右焦点分别为$$F_{1} \left(-c \， \ 0 \right) \quad， \ F_{2} \left( c \， \ 0 \right)$$，点$$N \left( c \，， \， \frac{a} {2} \right)$$在椭圆的外部，点$${{M}}$$是椭圆上的动点，满足$$| M F_{1} |+| M N | < {\frac{3} {2}} | F_{1} F_{2} |$$恒成立，则椭圆离心率$${{e}}$$的取值范围是（）
D
A.$$\left( 0 \，， \frac{\sqrt{2}} {2} \right)$$
B.$$\left( \frac{\sqrt{2}} {2} \;， 1 \right)$$
C.$$\left( \frac{\sqrt{2}} {2}， \frac{5} {6} \right)$$
D.$$\left( \frac{5} {6} \，， \， 1 \right)$$
5、['椭圆的对称性'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '直线与椭圆的综合应用'， '点与椭圆的位置关系'， '直线的斜率']正确率19.999999999999996%已知椭圆$$C : \frac{x^{2}} {2}+y^{2}=1$$，点$$M_{1}， M_{2}， \dots， ~ M_{5}$$为其长轴$${{A}{B}}$$的$${{6}}$$等分点，分别过这五点作斜率为$$k ( k \neq0 )$$的一组平行线，交椭圆$${{C}}$$于$$P_{1}， P_{2}， \ldots， ~ P_{1 0}$$，则直线$$A P_{1}， \， A P_{2}， \dots， \， \， A P_{1 0}$$这$${{1}{0}}$$条直线的斜率的乘积为（）
B
A.$$- \frac1 {1 6}$$
B.$$- \frac{1} {3 2}$$
C.$$\frac{1} {6 4}$$
D.$$\frac{1} {1 0 2 4}$$
6、['椭圆的离心率'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '直线与椭圆的综合应用'， '椭圆的其他性质'， '点与椭圆的位置关系']正确率60.0%已知椭圆$$\frac{x^{2}} {a^{2}} ~+~ \frac{y^{2}} {b^{2}}=1 ( a > b > 0 )，$$点$$P (-3， 1 )$$在直线$$x=-\frac{a^{2}} {c}$$上，过点$${{P}}$$且方向为$$\overrightarrow{a}=( 2，-5 )$$的光线，经过直线$${{y}{=}{−}{2}}$$反射后通过椭圆的左焦点，则这个椭圆的长轴长为$${{(}{)}}$$
D
A.$${{1}}$$
B.$${{2}}$$
C.$$\frac{\sqrt2} 2$$
D.$${{2}{\sqrt {3}}}$$
7、['两点间的斜率公式'， '点与椭圆的位置关系'， '利用基本不等式求最值'， '圆锥曲线的最值（范围）问题']正确率40.0%若点$$( m， n )$$在椭圆$$9 x^{2}+y^{2}=9$$上，则$$\frac{n} {m-3}$$的最小值为（）
D
A.$$- \frac{2 \sqrt2} 3$$
B.$$- \frac{2 \sqrt{3}} {3}$$
C.$$- \frac{\sqrt3} {2}$$
D.$$- \frac{3 \sqrt2} {4}$$
8、['椭圆的离心率'， '椭圆的对称性'， '点与椭圆的位置关系']正确率40.0%已知椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}} \!=\! 1 ( a \! > \! b \! > 0 )，$$直线$${{l}_{1}{，}{{l}_{2}}}$$分别平行于$${{x}}$$轴和$${{y}}$$轴，$${{l}_{1}}$$交椭圆于$${{A}{，}{B}}$$两点，$${{l}_{2}}$$交椭圆于$${{C}{，}{D}}$$两点，$${{l}_{1}{，}{{l}_{2}}}$$交于点$${{M}}$$，若$$| M A | \colon\， | M B | \colon\， | M C | \colon\， | M D |=6 \colon\， 2 \colon\， 1 \colon\， 3$$，则该椭圆的离心率为$${{(}{)}}$$
D
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{\sqrt2} {2}$$
D.$$\frac{\sqrt3} {2}$$
9、['椭圆的离心率'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '两条直线垂直'， '点与椭圆的位置关系']正确率60.0%分别过椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1$$的左$${、}$$右焦点$${{F}_{1}{、}{{F}_{2}}}$$所作的两条互相垂直的直线$${{l}_{1}{、}{{l}_{2}}}$$的交点在此椭圆的内部，则此椭圆的离心率的取值范围是$${{(}{)}}$$
B
A.$$( 0， 1 )$$
B.$$( 0， \frac{\sqrt{2}} {2} )$$
C.$$( \frac{\sqrt{2}} {2}， 1 )$$
D.$$[ 0， \frac{\sqrt{2}} {2} ]$$
10、['椭圆的离心率'， '点与椭圆的位置关系'， '圆锥曲线的存在性问题']正确率60.0%已知$${{F}_{1}{、}{{F}_{2}}}$$分别是椭圆$$C : \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 \， ( a > b > 0 )$$的左$${、}$$右焦点，椭圆$${{C}}$$上不存在点$${{P}}$$使$${{∠}{{F}_{1}}{P}{{F}_{2}}}$$为钝角，则椭圆$${{C}}$$的离心率的取值范围是
C
A.$$( \frac{\sqrt{2}} {2}， 1 )$$
B.$$[ \frac{1} {2}， 1 )$$
C.$$( 0， \frac{\sqrt{2}} {2} ]$$
D.$$( 0， \frac{1} {2} ]$$
1. 题目描述有误，集合A的定义不明确，无法解析。
2. 椭圆方程为$$\frac{x^2}{4}+y^2=1$$，焦点为$$F_1(-\sqrt{3},0)$$和$$F_2(\sqrt{3},0)$$。设点$$M(x,y)$$在椭圆上，满足$$\overrightarrow{MF_1} \cdot \overrightarrow{MF_2}=0$$，即$$(x+\sqrt{3})(x-\sqrt{3})+y^2=0$$，化简得$$x^2+y^2=3$$。结合椭圆方程解得$$y^2=\frac{2}{3}$$，因此点M到x轴的距离为$$\frac{2\sqrt{6}}{3}$$，选B。
3. 题目描述不完整，无法解析。
4. 点N在椭圆外部，满足$$\frac{c^2}{a^2}+\frac{(a/2)^2}{b^2}>1$$。由椭圆定义，$$|MF_1|+|MF_2|=2a$$，因此$$|MF_1|+|MN|<\frac{3}{2}|F_1F_2|=3c$$，即$$2a+|MN|-|MF_2|<3c$$。当M在椭圆右顶点时，$$|MN|-|MF_2|$$最大，代入得$$2a+\sqrt{(a-c)^2+(a/2)^2}-(a-c)<3c$$，解得$$e\in(\frac{\sqrt{2}}{2},1)$$，选B。
5. 椭圆长轴端点A(-√2,0)，B(√2,0)。设平行线为$$y=k(x-x_i)$$，与椭圆联立解得交点坐标。利用对称性和椭圆性质，可得斜率的乘积为$$-\frac{1}{32}$$，选B。
6. 由题意，P(-3,1)在准线$$x=-a^2/c$$上，即$$-3=-a^2/c$$。反射光线通过左焦点$$F_1(-c,0)$$，计算入射光线和反射光线的斜率关系，结合椭圆性质解得长轴长为$$2\sqrt{3}$$，选D。
7. 椭圆方程为$$9x^2+y^2=9$$，设$$\frac{n}{m-3}=k$$，即$$y=k(x-3)$$。与椭圆相切时k取极值，联立方程判别式为0，解得最小值为$$-\frac{3\sqrt{2}}{4}$$，选D。
8. 设M(x0,y0)，根据比例关系可得A,B,C,D坐标，代入椭圆方程并利用比例关系，解得离心率$$e=\frac{\sqrt{2}}{2}$$，选C。
9. 两条垂直直线交点在椭圆内部，即交点坐标满足$$\frac{x^2}{a^2}+\frac{y^2}{b^2}<1$$。计算交点坐标并代入不等式，解得$$e\in(0,\frac{\sqrt{2}}{2})$$，选B。
10. 当P在椭圆顶点时∠F1PF2最大，要使不存在钝角，需满足$$\cos\theta\geq0$$，解得$$e\in(0,\frac{\sqrt{2}}{2}]$$，选C。