.jpg)
正确率80.0%“方程$$\frac{x^{2}} {5-m}+\frac{y^{2}} {m+3}=1$$表示椭圆”是“$$- 3 < m < 5$$”的$${{(}{)}}$$
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分条件又不必要条件
2、['直线与椭圆的综合应用'， '椭圆的简单几何性质']正确率80.0%斜率为$${{k}}$$的直线$${{l}}$$与椭圆$${{C}}$$：$$\frac{x^{2}} {6}+\frac{y^{2}} {3}=1$$交于$${{A}}$$，$${{B}}$$两点，线段$${{A}{B}}$$的中点为$$M ( 2， m )$$，则$${{k}}$$的范围是$${{(}{)}}$$
A.$${{k}{<}{1}}$$
B.$$- \frac{1} {3} < k < \frac{1} {3}$$
C.$${{k}{<}{−}{1}}$$或$${{k}{>}{1}}$$
D.$$- \frac{2} {3} < k < \frac{2} {3}$$
3、['直线与椭圆的综合应用'， '椭圆的简单几何性质']正确率40.0%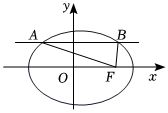
月光石不能频繁遇水，因为其主要成分是钾钠硅酸盐$${{.}}$$一块斯里兰卡月光石的截面可近似看成由半圆和半椭圆组成，如图所示，在平面直角坐标系，半圆的圆心在坐标原点，半圆所在的圆过椭圆的右焦点$$F ( 3， 0 )$$，椭圆的短轴与半圆的直径重合$${{.}}$$若直线$$y=\frac{3} {2} \sqrt{2}$$与半圆交于点$${{A}}$$，与半椭圆交于点$${{B}}$$，则$${{△}{A}{B}{F}}$$的面积是$${{(}{)}}$$
A.$$\frac{3 ( \sqrt{2}+1 )} {2}$$
B.$$\frac{9} {4} ( \sqrt{2}+1 )$$
C.$$\sqrt{2}+1$$
D.$$\frac{9} {2} ( \sqrt{2}+1 )$$
4、['椭圆的简单几何性质'， '双曲线的简单几何性质'， '直线与圆锥曲线的其他应用']正确率80.0%设$${{F}_{1}}$$，$${{F}_{2}}$$分别为椭圆$$C_{\colon} \ \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$与双曲线$$C_{1} \colon~ \frac{x^{2}} {a_{1}^{2}}-\frac{y^{2}} {b_{1}^{2}}=1 ( a_{1} > 0， b_{1} > 0 )$$的公共焦点，它们在第一象限内交于点$${{M}}$$，$$\angle F_{1} M F_{2}=6 0^{\， \circ}$$，若椭圆$${{C}}$$的离心率$$e \in[ \frac{\sqrt{2}} {2}， \frac{\sqrt{3}} {2} ]$$，则双曲线$${{C}_{1}}$$的离心率$${{e}_{1}}$$的取值范围为$${{(}{)}}$$
A.$$[ \frac{\sqrt{5}} {2}， \frac{\sqrt{6}} {2} ]$$
B.$$( \frac{\sqrt6} {2}，+\infty)$$
C.$$[ \frac{\sqrt6} {2}， \frac{\sqrt{1 4}} {2} ]$$
D.$$[ \frac{3 \sqrt{2}} {4}， \frac{\sqrt{6}} {2} ]$$
5、['椭圆的简单几何性质'， '与圆有关的轨迹问题']正确率80.0%已知$${{F}_{1}}$$，$${{F}_{2}}$$分别为椭圆$${{E}}$$：$$\frac{x^{2}} {9}+y^{2}=1$$的左、右焦点，$${{P}}$$是椭圆$${{E}}$$上一动点，$${{G}}$$点是三角形$${{P}{{F}_{1}}{{F}_{2}}}$$的重心，则点$${{G}}$$的轨迹方程为$${{(}{)}}$$
A.$$x^{2}+9 y^{2}=1$$
B.$$x^{2}+9 y^{2}=1 ( y \neq0 )$$
C.$$\frac{x^{2}} {8 1}+\frac{y^{2}} {9}=1$$
D.$$\frac{x^{2}} {8 1}+\frac{y^{2}} {9}=1 ( y \neq0 )$$
6、['椭圆的简单几何性质'， '三角函数与二次函数的综合应用'， '椭圆及其标准方程'， '两角和与差的余弦、正弦、正切公式']正确率40.0%已知椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$上有一个点$${{A}}$$，它关于原点的对称点为$${{B}}$$，点$${{F}}$$为椭圆的右焦点，且满足$$A F \perp B F$$，设$$\angle A B F=\theta$$，且$$\theta\in( {\frac{\pi} {1 2}}， {\frac{\pi} {3}} )$$，则椭圆的离心率的取值范围为$${{(}{)}}$$
A.$$( \frac{\sqrt{3}} {3}， \frac{\sqrt{6}} {2} ]$$
B.$$[ \frac{\sqrt2} {2}， \frac{\sqrt6} {3} )$$
C.$$( \frac{\sqrt{3}} {3}， \frac{\sqrt{6}} {2} )$$
D.$$( \frac{\sqrt2} {2}， \frac{\sqrt6} {3} )$$
7、['椭圆的简单几何性质']正确率40.0%已知椭圆方程为$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$，$$M ( 2， 1 )$$为椭圆内一点，以$${{M}}$$为中点的弦与椭圆交于点$${{A}}$$，$${{B}}$$，与$${{x}}$$轴交于点$${{P}}$$，线段$${{A}{B}}$$的中垂线与$${{x}}$$轴交于点$${{G}}$$，当$${{△}{G}{P}{M}}$$面积最小时，椭圆的离心率为$${{(}{)}}$$
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{\sqrt3} {2}$$
D.$$\frac{\sqrt{3}} {3}$$
8、['椭圆的简单几何性质']正确率40.0%已知椭圆$$C : \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 \， ( a > b > 0 )$$，$${{P}}$$是椭圆$${{C}}$$上的点，$$F_{1} \left(-c， 0 \right)， F_{2} \left( c， 0 \right)$$是椭圆$${{C}}$$的左右焦点，若$$\overrightarrow{P F_{1}} \cdot\overrightarrow{P F_{2}} \leq2 a c$$恒成立，则椭圆$${{C}}$$的离心率$${{e}}$$的取值范围是$${{(}{)}}$$
A.$$\left[ \frac{\sqrt{5}-1} {2}， 1 \right)$$
B.$$( 0， \sqrt{2}-1 ]$$
C.$$\left( 0， \frac{\sqrt{5}-1} {2} \right]$$
D.$$[ \sqrt{2}-1， 1 )$$
9、['椭圆的简单几何性质']正确率40.0%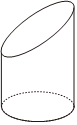
美学四大构件是：史诗、音乐、造型$${{(}}$$绘画、建筑等$${{)}}$$和数学$${{.}}$$素描是学习绘画的必要一步，它包括明暗素描和结构素描，而学习几何体结构素描是学习索描的重要一步$${{.}}$$某同学在画切面圆柱体$${{(}}$$用与圆柱底面不平行的平面去截圆柱，底面与截面之间的部分叫做切面圆柱体，原圆柱的母线被截面所截剩余的部分称为切面圆柱体的母线$${{)}}$$的过程中，发现“切面”是一个椭圆，若切面圆柱体的最长母线与最短母线所确定的平面截切面圆柱体得到的截面图形是一个底角为$${{6}{0}{°}}$$的直角梯形，设圆柱半径$${{r}{=}{1}}$$，则该椭圆的焦距为$${{(}{)}}$$
A.$$\frac{2 \sqrt{3}} {3}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{\sqrt3} {2}$$
D.$$\frac{1} {3}$$
10、['椭圆的简单几何性质']正确率80.0%已知椭圆$$\frac{x^{2}} {2 5}+\frac{y^{2}} {1 6}=1$$的左、右焦点分别为$${{F}_{1}}$$、$${{F}_{2}}$$，点$${{P}}$$在椭圆上，若$$| P F_{1} |=6$$，则$${{△}{P}{{F}_{1}}{{F}_{2}}}$$的面积为$${{(}{)}}$$
A.$${{8}}$$
B.$${{8}{\sqrt {2}}}$$
C.$${{1}{6}}$$
D.$${{1}{6}{\sqrt {2}}}$$
1. 方程 $$\frac{x^{2}}{5-m} + \frac{y^{2}}{m+3} = 1$$ 表示椭圆的条件是分母均为正且不相等，即 $$5 - m > 0$$ 且 $$m + 3 > 0$$ 且 $$5 - m \neq m + 3$$。解得 $$-3 < m < 5$$ 且 $$m \neq 1$$。题目中 $$-3 < m < 5$$ 是表示椭圆的必要条件，但不是充分条件（因为 $$m = 1$$ 时方程表示圆）。因此，答案是 **B.必要不充分条件**。
2. 设直线 $$l$$ 的方程为 $$y = kx + c$$，与椭圆 $$C$$ 联立后得到关于 $$x$$ 的二次方程。由于 $$M(2, m)$$ 是弦 $$AB$$ 的中点，利用中点坐标公式和判别式条件，可以推导出 $$k$$ 的范围。最终计算得到 $$k$$ 的范围是 $$- \frac{1}{3} < k < \frac{1}{3}$$，因此答案是 **B**。
3. 半圆的方程为 $$x^2 + y^2 = 9$$（因为半圆过点 $$F(3, 0)$$），半椭圆的方程为 $$\frac{x^2}{9} + \frac{y^2}{b^2} = 1$$（短轴与半圆直径重合，故 $$b = 3$$）。直线 $$y = \frac{3\sqrt{2}}{2}$$ 与半圆交于点 $$A(-\frac{3\sqrt{2}}{2}, \frac{3\sqrt{2}}{2})$$，与半椭圆交于点 $$B(\frac{3\sqrt{2}}{2}, \frac{3\sqrt{2}}{2})$$。计算三角形 $$ABF$$ 的面积，结果为 $$\frac{9}{4}(\sqrt{2} + 1)$$，因此答案是 **B**。
4. 椭圆和双曲线的公共焦点为 $$F_1$$ 和 $$F_2$$，设 $$|F_1F_2| = 2c$$。在椭圆中，离心率 $$e = \frac{c}{a}$$；在双曲线中，离心率 $$e_1 = \frac{c}{a_1}$$。利用余弦定理和椭圆离心率的范围，可以推导出双曲线离心率 $$e_1$$ 的范围为 $$\left[ \frac{\sqrt{6}}{2}, \frac{\sqrt{14}}{2} \right]$$，因此答案是 **C**。
5. 椭圆 $$E$$ 的焦点为 $$F_1(-2\sqrt{2}, 0)$$ 和 $$F_2(2\sqrt{2}, 0)$$。设点 $$P(x, y)$$ 在椭圆上，重心 $$G$$ 的坐标为 $$\left( \frac{x}{3}, \frac{y}{3} \right)$$。将 $$P$$ 的坐标代入椭圆方程，得到 $$G$$ 的轨迹方程为 $$x^2 + 9y^2 = 1$$（$$y \neq 0$$），因此答案是 **B**。
6. 设点 $$A(x, y)$$，则 $$B(-x, -y)$$。条件 $$AF \perp BF$$ 转化为向量点积为零，得到 $$x^2 + y^2 = c^2$$。结合椭圆方程和角度 $$\theta$$ 的范围，可以推导出离心率 $$e$$ 的范围为 $$\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{6}}{3} \right)$$，因此答案是 **D**。
7. 设椭圆方程为 $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$，弦 $$AB$$ 的斜率为 $$k$$，中点 $$M(2, 1)$$。利用点差法和判别式条件，可以求出 $$k$$ 与 $$a$$、$$b$$ 的关系。进一步分析三角形 $$GPM$$ 的面积最小值条件，得到离心率 $$e = \frac{\sqrt{2}}{2}$$，因此答案是 **B**。
8. 设点 $$P(x, y)$$ 在椭圆上，向量 $$\overrightarrow{PF_1} = (-c - x, -y)$$，$$\overrightarrow{PF_2} = (c - x, -y)$$。点积条件 $$\overrightarrow{PF_1} \cdot \overrightarrow{PF_2} \leq 2ac$$ 化简后得到 $$x^2 + y^2 \geq c^2 - 2ac$$。结合椭圆方程，推导出离心率 $$e$$ 的范围为 $$\left( 0, \frac{\sqrt{5} - 1}{2} \right]$$，因此答案是 **C**。
9. 切面圆柱体的截面是椭圆，圆柱半径 $$r = 1$$。根据题意，梯形的底角为 $$60^\circ$$，可以求出椭圆的半长轴 $$a = \frac{2\sqrt{3}}{3}$$，半短轴 $$b = 1$$。焦距 $$2c = 2\sqrt{a^2 - b^2} = \frac{2\sqrt{3}}{3}$$，因此答案是 **A**。
10. 椭圆 $$\frac{x^2}{25} + \frac{y^2}{16} = 1$$ 的焦点为 $$F_1(-3, 0)$$ 和 $$F_2(3, 0)$$。点 $$P$$ 满足 $$|PF_1| = 6$$，利用椭圆定义 $$|PF_1| + |PF_2| = 10$$，得到 $$|PF_2| = 4$$。利用余弦定理和面积公式，计算得到三角形面积为 $$8$$，因此答案是 **A**。