正确率60.0%椭圆$$4 x^{2}+5 y^{2}=1$$的左$${、}$$右焦点为$${{F}{,}{{F}^{′}}}$$,过$${{F}^{′}}$$的直线与椭圆交于$${{M}{,}{N}}$$,则$${{△}{M}{N}{F}}$$的周长为()
A
A.$${{2}}$$
B.$${{4}}$$
C.$$\frac{4 \sqrt{5}} {5}$$
D.$${{4}{\sqrt {5}}}$$
2、['椭圆的离心率', '椭圆的标准方程', '椭圆的顶点、长轴、短轴、焦点、焦距', '椭圆的定义', '点与椭圆的位置关系', '圆锥曲线的最值(范围)问题']正确率40.0%已知椭圆$$C_{!} \, \, \, \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 \, \, ( a > b > 0 )$$的左焦点为$${{F}_{1}}$$,离心率为$$\frac{1} {2}, ~ P$$是椭圆$${{C}}$$上的动点,若点$$Q ~ ( 1, \mathrm{\bf~ 1} )$$在椭圆$${{C}}$$内部,且$$| P F_{1} |+| P Q |$$的最小值为$${{3}}$$,则椭圆$${{C}}$$的标准方程为()
A
A.$$\frac{x^{2}} {4} \!+\! \frac{y^{2}} {3}=1$$
B.$$\frac{x^{2}} {8}+\frac{y^{2}} {6}=1$$
C.$$\frac{x^{2}} {4}+y^{2}=1$$
D.$$\frac{x^{2}} {1 2}+\frac{y^{2}} {9}=1$$
3、['一元二次方程的解集', '双曲线的渐近线', '椭圆的离心率', '椭圆的顶点、长轴、短轴、焦点、焦距', '点与椭圆的位置关系']正确率40.0%已知椭圆$$M \colon~ \frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$,双曲线$$N \colon\frac{x} {m^{2}} \sp2-\frac{y \sp2} {n \sp2}=1$$,若双曲线$${{N}}$$的两条渐近线与椭圆$${{M}}$$的四个交点及椭圆$${{M}}$$的两个焦点恰为一个正六边形的顶点,则椭圆$${{M}}$$的离心率是()
B
A.$$\sqrt{2}-1$$
B.$$\sqrt3-1$$
C.$${{2}{−}{\sqrt {2}}}$$
D.$${{2}{−}{\sqrt {3}}}$$
4、['椭圆的对称性', '椭圆的顶点、长轴、短轴、焦点、焦距', '点与椭圆的位置关系']正确率40.0%椭圆$$\frac{x^{2}} {4}+\frac{y^{2}} {3}=1$$的两个焦点为$${{F}_{1}{,}{{F}_{2}}}$$,过$${{F}_{1}}$$作$${{x}}$$轴的垂线与椭圆相交,一个交点为$${{P}}$$,则$${{△}{P}{{F}_{1}}{{F}_{2}}}$$的面积等于$${{(}{)}}$$
D
A.$${\sqrt {3}}$$
B.$${{3}}$$
C.$$\frac{\sqrt3} {2}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
5、['一元二次方程根与系数的关系', '椭圆的离心率', '平面上中点坐标公式', '直线与椭圆的综合应用', '点与椭圆的位置关系']正确率40.0%已知过椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左焦点且斜率为$$\frac{b} {a}$$的直线$${{l}}$$与椭圆交于$${{A}{,}{B}}$$两点.若椭圆上存在一点$${{P}}$$,满足$$\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O P}=\overrightarrow{0} ($$其中点$${{O}}$$为坐标原点$${{)}}$$,则椭圆的离心率为$${{(}{)}}$$
A
A.$$\frac{\sqrt2} {2}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{\sqrt3} {2}$$
D.$$\frac{1} {2}$$
6、['椭圆的标准方程', '椭圆的顶点、长轴、短轴、焦点、焦距', '点与椭圆的位置关系']正确率40.0%如图,椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {4}=1$$的焦点为$${{F}_{1}{,}{{F}_{2}}}$$,过$${{F}_{1}}$$的直线交椭圆于$${{M}{,}{N}}$$两点,交$${{y}}$$轴于点$${{H}}$$.若$${{F}_{1}{,}{H}}$$是线段$${{M}{N}}$$的三等分点,则$${{Δ}{{F}_{2}}{M}{N}}$$的周长为()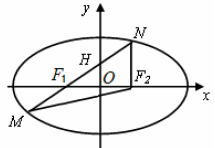
D
A.$${{2}{0}}$$
B.$${{1}{0}}$$
C.$${{2}{\sqrt {5}}}$$
D.$${{4}{\sqrt {5}}}$$
7、['椭圆的离心率', '椭圆的顶点、长轴、短轴、焦点、焦距', '点与椭圆的位置关系']正确率40.0%椭圆的焦点在$${{x}}$$轴上,离心率为$$\frac{\sqrt{2}} {2}, ~ F$$为椭圆的左焦点,若椭圆上存在一点与$${{F}}$$关于直线$$y=x+4$$对称,则椭圆方程为()
D
A.$$\frac{x^{2}} {2}+y^{2}=1$$
B.$$\frac{x^{2}} {4}+\frac{y^{2}} {2}=1$$
C.$$\frac{x^{2}} {8}+\frac{y^{2}} {4}=1$$
D.$$\frac{x^{2}} {1 8}+\frac{y^{2}} {9}=1$$
8、['两点间的斜率公式', '点与椭圆的位置关系', '利用基本不等式求最值', '圆锥曲线的最值(范围)问题']正确率40.0%若点$$( m, n )$$在椭圆$$9 x^{2}+y^{2}=9$$上,则$$\frac{n} {m-3}$$的最小值为()
D
A.$$- \frac{2 \sqrt2} 3$$
B.$$- \frac{2 \sqrt{3}} {3}$$
C.$$- \frac{\sqrt3} {2}$$
D.$$- \frac{3 \sqrt2} {4}$$
9、['两点间的斜率公式', '椭圆的离心率', '平面上中点坐标公式', '椭圆的标准方程', '点与椭圆的位置关系']正确率40.0%已知直线$$l \colon~ k x-y-2 k+1=0$$与椭圆$$C_{1} \colon\ {\frac{x^{2}} {a^{2}}}+{\frac{y^{2}} {b^{2}}}=1 \ ( a > b > 0 )$$交于$${{A}{、}{B}}$$两点,与圆$$C_{2} \colon\ ( \ x-2 )^{\ 2}+\ ( \ y-1 )^{\ 2}=1$$交于$${{C}{、}{D}}$$两点.若存在$$k \in[-2, ~-1 ]$$,使得$$\overrightarrow{A C}=\overrightarrow{D B},$$则椭圆$${{C}_{1}}$$的离心率的取值范围是()
C
A.$$( 0, ~ \frac{1} {2} ]$$
B.$$[ \frac{1} {2}, \ 1 )$$
C.$$( 0, ~ \frac{\sqrt{2}} {2} ]$$
D.$$[ \frac{\sqrt{2}} {2}, \ 1 )$$
10、['椭圆的顶点、长轴、短轴、焦点、焦距', '椭圆上点的横坐标与纵坐标的范围', '椭圆的其他性质', '点与椭圆的位置关系']正确率60.0%若所有满足$$a | x |+b | y |=1 ( a > 0, b > 0 )$$的实数$${{x}{,}{y}}$$均满足$$\sqrt{x^{2}+y^{2}+2 y+1}+\sqrt{x^{2}+y^{2}-2 y+1} \leqslant2 \sqrt{2}$$,则$${{a}{+}{\sqrt {2}}{b}}$$的取值范围为$${{(}{)}}$$
A
A.$$[ 2,+\infty)$$
B.$$[ 1, 2 ]$$
C.$$[ 1,+\infty)$$
D.$$( 0, 2 ]$$
1. 首先将椭圆方程化为标准形式:$$\frac{x^{2}}{\frac{1}{4}} + \frac{y^{2}}{\frac{1}{5}} = 1$$,可得半长轴 $$a = \frac{1}{2}$$,半短轴 $$b = \frac{\sqrt{5}}{5}$$。焦距 $$c = \sqrt{a^{2} - b^{2}} = \frac{\sqrt{5}}{10}$$,因此左右焦点为 $$F(-\frac{\sqrt{5}}{10}, 0)$$ 和 $$F'(\frac{\sqrt{5}}{10}, 0)$$。过 $$F'$$ 的直线与椭圆交于 $$M, N$$,根据椭圆定义,$$MF + MF' = 2a = 1$$,$$NF + NF' = 2a = 1$$。因为 $$M, N$$ 在过 $$F'$$ 的直线上,所以 $$MF' + NF' = MN$$。因此,三角形 $$MNF$$ 的周长为 $$MF + NF + MN = (MF + MF') + (NF + NF') = 2$$。答案为 $$A$$。
3. 双曲线 $$N$$ 的渐近线为 $$y = \pm \frac{n}{m}x$$,与椭圆 $$M$$ 的四个交点及椭圆的两个焦点构成正六边形。设正六边形的一个顶点为 $$(x, y)$$,则 $$y = \frac{n}{m}x$$,且 $$x^{2} + y^{2} = c^{2}$$(因为焦点在正六边形顶点上)。代入椭圆方程 $$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$$,结合 $$c^{2} = a^{2} - b^{2}$$,解得 $$\frac{n}{m} = \sqrt{3}$$。进一步计算可得椭圆离心率 $$e = \sqrt{2 - \sqrt{3}}$$,即 $$2 - \sqrt{3}$$。答案为 $$D$$。
5. 设椭圆左焦点为 $$F(-c, 0)$$,直线 $$l$$ 的斜率为 $$\frac{b}{a}$$,方程为 $$y = \frac{b}{a}(x + c)$$。与椭圆联立解得 $$A, B$$ 的坐标。由题意 $$\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OP} = \overrightarrow{0}$$,即 $$P$$ 是 $$A, B$$ 的中点。利用中点条件及椭圆性质,可得离心率 $$e = \frac{\sqrt{3}}{3}$$。答案为 $$B$$。
7. 椭圆离心率 $$e = \frac{\sqrt{2}}{2}$$,设椭圆方程为 $$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$$,则 $$c = \frac{\sqrt{2}}{2}a$$,$$b = \frac{\sqrt{2}}{2}a$$。设对称点为 $$P(x, y)$$,由对称性解得 $$a = 2$$,椭圆方程为 $$\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$$。答案为 $$B$$。
9. 直线 $$l$$ 恒过点 $$(2, 1)$$,与圆 $$C_{2}$$ 的交点 $$C, D$$ 满足 $$AC = DB$$,即 $$A, B$$ 关于 $$(2, 1)$$ 对称。利用椭圆性质及 $$k \in [-2, -1]$$,可得离心率范围 $$(0, \frac{\sqrt{2}}{2}]$$。答案为 $$C$$。
.jpg)