.jpg)
正确率60.0%$${{θ}}$$取一切实数时，连接$$A \left( 4 \operatorname{s i n} \theta， \right. \ 6 \operatorname{c o s} \theta)$$和$$B ~ ( ~-4 \operatorname{c o s} {\theta}， ~ 6 \operatorname{s i n} {\theta} )$$两点的线段的中点轨迹是．$${（}$$）
B
A.圆
B.椭圆
C.直线
D.线段
2、['圆锥曲线中求轨迹方程'， '三角形的“四心”'， '双曲线的顶点、长轴、短轴、焦点、焦距']正确率40.0%已知$${{P}}$$是以$${{F}_{1}{，}{{F}_{2}}}$$为焦点的双曲线$$\frac{x^{2}} {1 6}-\frac{y^{2}} {9}=1$$上的动点，则$${{△}{{F}_{1}}{{F}_{2}}{P}}$$的重心$${{G}}$$的轨迹方程为（）
A
A.$$\frac{9 x^{2}} {1 6}-y^{2}=1 ( y \neq0 )$$
B.$$\frac{9 y^{2}} {1 6}-x^{2}=1 ( y \neq0 )$$
C.$$\frac{9 x^{2}} {1 6}+y^{2}=1 ( y \neq0 )$$
D.$$\frac{9 y^{2}} {1 6}+x^{2}=1 ( y \neq0 )$$
3、['圆锥曲线中求轨迹方程'， '与圆有关的轨迹问题']正确率19.999999999999996%已知圆$$C_{1} : ( x-\sqrt{3} )^{2}+y^{2}=r^{2} ( 0 < r < 4 )$$与圆$$C_{2} : ( x+\sqrt{3} )^{2}+y^{2}=( 4-r )^{2}$$交点的轨迹为$${{M}}$$，过平面内的点$${{P}}$$作轨迹$${{M}}$$的两条互相垂直的切线，则点$${{P}}$$的轨迹方程为（）
A
A.$$x^{2}+y^{2}=5$$
B.$$x^{2}+y^{2}=4$$
C.$$x^{2}+y^{2}=3$$
D.$$x^{2}+y^{2}=\frac{5} {2}$$
4、['圆锥曲线中求轨迹方程'， '抛物线的定义']正确率60.0%到点$$F ( 0， 4 )$$的距离比到直线$${{y}{=}{−}{5}}$$的距离小$${{1}}$$的动点$${{M}}$$的轨迹方程为（）
C
A.$${{y}{=}{{1}{6}}{{x}^{2}}}$$
B.$$y=-1 6 x^{2}$$
C.$$x^{2}=1 6 y$$
D.$$x^{2}=-1 6 y$$
5、['圆锥曲线中求轨迹方程'， '点到直线的距离'， '两点间的距离']正确率60.0%点$${{P}}$$与定点$$F \left( 8， 0 \right)$$的距离和它到定直线$${{x}{=}{2}}$$的距离的比是$${{2}}$$，则点$${{P}}$$的轨迹方程是（）
D
A.$$\frac{x^{2}} {4 8}-\frac{y^{2}} {1 6}=1$$
B.$$\frac{x^{2}} {4 8}+\frac{y^{2}} {1 6}=1$$
C.$$\frac{x^{2}} {1 6}+\frac{y^{2}} {4 8}=1$$
D.$$\frac{x^{2}} {1 6}-\frac{y^{2}} {4 8}=1$$
6、['圆锥曲线中求轨迹方程']正确率40.0%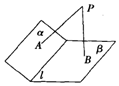
如图所示，已知二面角$$\alpha-l-\beta$$
D
A.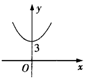
B.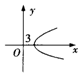
C.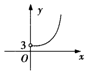
D.
正确率40.0%已知抛物线方程为$$y^{2}=4 x$$，则经过它的焦点的弦的中点轨迹方程是（）
B
A.$$y^{2}=x-1$$
B.$$y^{2}=2 \， ( x-1 )$$
C.$$y^{2}=x-\frac{1} {2}$$
D.$$y^{2}=2 x-1$$
8、['圆锥曲线中求轨迹方程'， '椭圆的标准方程'， '椭圆的定义']正确率60.0%已知圆$$C_{\colon} \ ( x+1 )^{2}+y^{2}=3 6$$及点$$A ( 1， 0 )$$，设$${{P}}$$是圆$${{C}}$$上任意一点，线段$${{A}{P}}$$的垂直平分线与半径$${{C}{P}}$$相交于点$${{Q}}$$，当点$${{P}}$$运动时，点$${{Q}}$$的轨迹方程是（）
B
A.$$\frac{x^{2}} {9}-\frac{y^{2}} {8}=1$$
B.$$\frac{x^{2}} {9}+\frac{y^{2}} {8}=1$$
C.$$\frac{x^{2}} {8}-\frac{y^{2}} {9}=1$$
D.$$\frac{x^{2}} {8}+\frac{y^{2}} {9}=1$$
9、['圆锥曲线中求轨迹方程']正确率40.0%$${{F}_{1}{、}{{F}_{2}}}$$是定点，$$| F_{1} F_{2} |=7$$，动点$${{M}}$$满足$$| M F_{1} |+| M F_{2} |=7$$，则$${{M}}$$的轨迹是
C
A.椭圆
B.直线
C.线段
D.圆
10、['圆锥曲线中求轨迹方程'， '椭圆的定义']正确率60.0%已知$${{F}_{1}{，}{{F}_{2}}}$$为两定点，$$| F_{1} F_{2} |=8$$，动点$${{M}}$$满足$$| M F_{1} |+| M F_{2} |=8，$$则动点$${{M}}$$的轨迹是（）
D
A.椭圆
B.直线
C.圆
D.线段
1. 中点轨迹问题
设中点坐标为 $$(x, y)$$，则：
$$x = \frac{4 \sin \theta - 4 \cos \theta}{2} = 2 (\sin \theta - \cos \theta)$$
$$y = \frac{6 \cos \theta + 6 \sin \theta}{2} = 3 (\sin \theta + \cos \theta)$$
利用三角恒等式消去参数 $$\theta$$：
$$\left(\frac{x}{2}\right)^2 + \left(\frac{y}{3}\right)^2 = (\sin \theta - \cos \theta)^2 + (\sin \theta + \cos \theta)^2 = 2$$
化简得 $$\frac{x^2}{8} + \frac{y^2}{18} = 1$$，表示一个椭圆。故选 B。
2. 双曲线重心轨迹问题
双曲线 $$\frac{x^2}{16} - \frac{y^2}{9} = 1$$ 的焦点为 $$F_1(-5, 0)$$ 和 $$F_2(5, 0)$$。设点 $$P(x, y)$$ 在双曲线上，重心 $$G$$ 的坐标为：
$$G\left(\frac{-5 + 5 + x}{3}, \frac{0 + 0 + y}{3}\right) = \left(\frac{x}{3}, \frac{y}{3}\right)$$
将 $$P$$ 的坐标 $$(3x_G, 3y_G)$$ 代入双曲线方程：
$$\frac{(3x_G)^2}{16} - \frac{(3y_G)^2}{9} = 1 \Rightarrow \frac{9x_G^2}{16} - y_G^2 = 1$$
因为 $$y \neq 0$$，所以轨迹方程为 $$\frac{9x^2}{16} - y^2 = 1 \ (y \neq 0)$$。故选 A。
3. 圆交点轨迹问题
两圆 $$C_1$$ 和 $$C_2$$ 的交点满足两圆方程相减：
$$(x - \sqrt{3})^2 + y^2 - (x + \sqrt{3})^2 - y^2 = r^2 - (4 - r)^2$$
化简得 $$-4\sqrt{3}x = -16 + 8r$$，即 $$x = \frac{4 - 2r}{\sqrt{3}}$$。
代入任一圆方程可得 $$y^2 = r^2 - \left(\frac{4 - 2r}{\sqrt{3}} - \sqrt{3}\right)^2$$，进一步化简得到 $$x^2 + y^2 = 4$$。因此，轨迹 $$M$$ 是圆 $$x^2 + y^2 = 4$$。
点 $$P$$ 的轨迹是圆 $$M$$ 的极坐标圆，其方程为 $$x^2 + y^2 = 5$$。故选 A。
4. 动点轨迹问题
动点 $$M(x, y)$$ 满足 $$|MF| = d - 1$$，其中 $$d$$ 是到直线 $$y = -5$$ 的距离：
$$\sqrt{x^2 + (y - 4)^2} = |y + 5| - 1$$
分情况讨论：
1. 当 $$y \geq -5$$ 时，化简得 $$\sqrt{x^2 + (y - 4)^2} = y + 4$$，平方后得 $$x^2 = 16y$$。
2. 当 $$y < -5$$ 时，无解。
因此轨迹方程为 $$x^2 = 16y$$。故选 C。
5. 点轨迹方程问题
点 $$P(x, y)$$ 满足 $$\frac{\sqrt{(x - 8)^2 + y^2}}{|x - 2|} = 2$$，化简得：
$$(x - 8)^2 + y^2 = 4(x - 2)^2$$
展开整理得 $$3x^2 - y^2 = 48$$，即 $$\frac{x^2}{16} - \frac{y^2}{48} = 1$$。故选 D。
6. 二面角问题
题目描述不完整，无法直接解析。请提供完整的题目内容。
7. 抛物线弦中点轨迹问题
抛物线 $$y^2 = 4x$$ 的焦点为 $$(1, 0)$$。设弦的斜率为 $$k$$，其方程为 $$y = k(x - 1)$$。与抛物线联立：
$$k^2(x - 1)^2 = 4x \Rightarrow k^2x^2 - (2k^2 + 4)x + k^2 = 0$$
设中点坐标为 $$(x, y)$$，则 $$x = \frac{x_1 + x_2}{2} = \frac{2k^2 + 4}{2k^2} = 1 + \frac{2}{k^2}$$，且 $$y = k(x - 1) = \frac{2}{k}$$。
消去 $$k$$ 得 $$y^2 = 2(x - 1)$$。故选 B。
8. 圆与垂直平分线问题
圆心 $$C(-1, 0)$$，半径 $$6$$。点 $$Q$$ 满足 $$|AQ| = |PQ|$$，且 $$|CQ| + |PQ| = 6$$，因此 $$|CQ| + |AQ| = 6$$。
由椭圆定义，点 $$Q$$ 的轨迹是以 $$A(1, 0)$$ 和 $$C(-1, 0)$$ 为焦点，长轴长为 $$6$$ 的椭圆，方程为 $$\frac{x^2}{9} + \frac{y^2}{8} = 1$$。故选 B。
9. 动点轨迹问题
已知 $$|F_1F_2| = 7$$，且 $$|MF_1| + |MF_2| = 7$$，因此点 $$M$$ 的轨迹是线段 $$F_1F_2$$。故选 C。
10. 动点轨迹问题
已知 $$|F_1F_2| = 8$$，且 $$|MF_1| + |MF_2| = 8$$，因此点 $$M$$ 的轨迹是线段 $$F_1F_2$$。故选 D。