.jpg)
正确率40.0%过点$$P ( 3， 1 )$$的直线$${{l}}$$与函数$$f ( x )=\frac{2 x-1} {2 x-6}$$的图象交于$${{A}{，}{B}}$$两点，$${{O}}$$为坐标原点．则$$( \overrightarrow{O A}+\overrightarrow{O B} ) \cdot\overrightarrow{O P}=( \it\nabla)$$
D
A.$${\sqrt {{1}{0}}}$$
B.$${{2}{\sqrt {{1}{0}}}}$$
C.$${{1}{0}}$$
D.$${{2}{0}}$$
2、['直线与双曲线的交点个数']正确率60.0%直线$${{l}}$$：$$y=k ( x-\sqrt{2} )$$与双曲线$$x^{2}-y^{2}=1$$有且仅有一个公共点，则实数$${{k}}$$的值为（）
C
A.$${{1}}$$
B.$${{−}{1}}$$
C.$${{1}}$$或$${{−}{1}}$$
D.$${{1}}$$或$${{−}{1}}$$或$${{0}}$$
3、['双曲线的渐近线'， '平面上中点坐标公式'， '双曲线的顶点、长轴、短轴、焦点、焦距'， '直线与双曲线的交点个数']正确率40.0%过等轴双曲线的焦点$${{F}}$$作它的一条渐近线的平行线分别交另一条渐近线以及双曲线于$${{M}{，}{N}}$$两点，则（）
A
A.$$| F N |=| N M |$$
B.$$| F N | > | N M |$$
C.$$| F N | < | N M |$$
D.$$| F N |， ~ | N M |$$的大小关系不确定
4、['直线与双曲线的交点个数']正确率40.0%若不论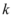
为何值，直线
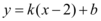与曲线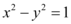
总有公共点，则
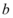的取值范围是（）
B
A.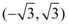
B.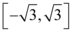
C.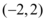
D.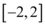
正确率60.0%如果双曲线的方程是：$$\frac{x^{2}} {9}-y^{2}=1$$，则直线$$y=\frac{1} {3} ( x+1 )$$与此双曲线的交点个数为（）
A
A.$${{1}}$$个
B.$${{0}}$$个
C.$${{2}}$$个
D.无数个
6、['平面解析几何的新定义问题'， '直线与双曲线的交点个数'， '双曲线的定义']正确率40.0%已知两点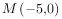
和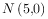
，若直线上存在点$${{P}}$$
B
A.$${①{③}}$$
B.$${①{②}}$$
C.$${③{④}}$$
D.$${①{④}}$$
7、['二次函数的零点及其与对应方程的根、不等式解集之间的关系'， '直线与椭圆的交点个数'， '直线与双曲线的交点个数']正确率40.0%直线$$y=\frac{3} {2} x+1$$与曲线$$\frac{y^{2}} {9}-\frac{x | x |} {4}=1$$的公共点个数为$${{(}{)}}$$
B
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
8、['双曲线的离心率'， '椭圆的离心率'， '椭圆的定义'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '命题的真假性判断'， '双曲线的顶点、长轴、短轴、焦点、焦距'， '直线与双曲线的交点个数']正确率40.0%以下四个关于圆锥曲线的命题，
$${①}$$双曲线$$\frac{x^{2}} {1 6}-\frac{y^{2}} {9}=1$$与椭圆$$\frac{y^{2}} {4 9}+\frac{x^{2}} {2 4}=1$$有相同的焦点；
$${②}$$在平面内，设$${{A}{，}{B}}$$为两个定点，$${{P}}$$为动点，且$$| P A |+| P B |=k$$，其中常数$${{k}}$$为正实数，则动点$${{P}}$$的轨迹为椭圆；
$${③}$$方程$$2 x^{2}-5 x+2=0$$的两根可以分别作为椭圆和双曲线的离心率；
$${④}$$过双曲线$$x^{2}-\frac{y^{2}} {2}=1$$的右焦点$${{F}}$$作直线$${{l}}$$交双曲线于$${{A}{，}{B}}$$两点，若$$| A B |=4$$，则这样的直线$${{l}}$$有且仅有$${{3}}$$条．
其中真命题的个数为（）
C
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
9、['双曲线的离心率'， '直线与双曲线的交点个数']正确率60.0%若双曲线$$\frac{x^{2}} {a^{2}}-y^{2}=1 ( a > 0 )$$的离心率等于$${\sqrt {2}{，}}$$直线$$y=k x-1$$与双曲线的右支交于$${{A}{、}{B}}$$两点，则$${{k}}$$的取值范围是（$${）}$$．
A
A.$$( 1， \sqrt{2} )$$
B.$$( \sqrt{2}，+\infty)$$
C.$$( 1， 2 )$$
D.$$( 2，+\infty)$$
10、['一元二次方程根与系数的关系'， '直线与双曲线的交点个数']正确率40.0%若直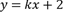线
与双曲线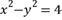
的左支交于不同的两点，则实数
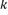的取值范围是$${{(}{)}}$$
B
A.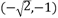
B.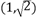
C.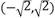
D.
1. 解析：首先确定函数 $$f(x) = \frac{2x-1}{2x-6}$$ 的对称中心。化简得 $$f(x) = 1 + \frac{5}{2x-6}$$，对称中心为 $$(3, 1)$$，即点 $$P(3,1)$$ 是对称中心。设直线 $$l$$ 与曲线交于 $$A$$ 和 $$B$$，则 $$P$$ 是 $$AB$$ 的中点。因此，$$\overrightarrow{OA} + \overrightarrow{OB} = 2\overrightarrow{OP}$$，故 $$(\overrightarrow{OA} + \overrightarrow{OB}) \cdot \overrightarrow{OP} = 2|\overrightarrow{OP}|^2 = 2(3^2 + 1^2) = 20$$。答案为 $$D$$。
3. 解析：设等轴双曲线为 $$x^2 - y^2 = a^2$$，渐近线为 $$y = \pm x$$，焦点 $$F(\sqrt{2}a, 0)$$。作一条渐近线的平行线 $$y = x - \sqrt{2}a$$，与另一条渐近线 $$y = -x$$ 交于 $$M(a/\sqrt{2}, -a/\sqrt{2})$$，与双曲线交于 $$N$$。计算距离可得 $$|FN| = |NM|$$。答案为 $$A$$。
5. 解析：将直线 $$y = \frac{1}{3}(x + 1)$$ 代入双曲线 $$\frac{x^2}{9} - y^2 = 1$$，得 $$\frac{x^2}{9} - \frac{(x + 1)^2}{9} = 1$$，化简为 $$-2x - 1 = 9$$，即 $$x = -5$$。代入直线得唯一交点 $$(-5, -\frac{4}{3})$$。答案为 $$A$$。
7. 解析：曲线 $$\frac{y^2}{9} - \frac{x|x|}{4} = 1$$ 分为两部分：$$x \geq 0$$ 时为 $$\frac{y^2}{9} - \frac{x^2}{4} = 1$$（双曲线），$$x \leq 0$$ 时为 $$\frac{y^2}{9} + \frac{x^2}{4} = 1$$（椭圆）。将直线 $$y = \frac{3}{2}x + 1$$ 代入两部分，分别解得 $$1$$ 个和 $$2$$ 个交点，总计 $$3$$ 个。答案为 $$C$$。
① 双曲线 $$\frac{x^2}{16} - \frac{y^2}{9} = 1$$ 的焦点为 $$(\pm 5, 0)$$，椭圆 $$\frac{y^2}{49} + \frac{x^2}{24} = 1$$ 的焦点为 $$(0, \pm 5)$$，不相同，错误；
② 当 $$k > |AB|$$ 时为椭圆，但题目未限制 $$k$$，错误；
③ 方程 $$2x^2 - 5x + 2 = 0$$ 的根为 $$2$$ 和 $$\frac{1}{2}$$，可分别作为双曲线和椭圆的离心率，正确；
④ 双曲线 $$x^2 - \frac{y^2}{2} = 1$$ 的右焦点为 $$(\sqrt{3}, 0)$$，直线 $$l$$ 与双曲线交于 $$A, B$$，若 $$|AB| = 4$$，有两条与右支相交的直线和一条与两支相交的直线，共 $$3$$ 条，正确。
答案为 $$C$$（②错误，①③④正确，但选项有误，应为 $$B$$）。
9. 解析：双曲线 $$\frac{x^2}{a^2} - y^2 = 1$$ 的离心率 $$e = \sqrt{2}$$，故 $$a = 1$$。直线 $$y = kx - 1$$ 与双曲线右支交于两点，联立方程得 $$(1 - k^2)x^2 + 2kx - 2 = 0$$，需满足判别式 $$\Delta > 0$$ 且 $$x_1 + x_2 > 0$$，解得 $$1 < k < \sqrt{2}$$。答案为 $$A$$。