.jpg)
正确率80.0%设$$6^{m}=2， \， \， 6^{n}=3，$$则$$m^{2}+n^{2}+2 m n=$$（）
B
A.$$\frac{1} {2}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
2、['有理数指数幂的运算性质'， '指数与对数的关系']正确率60.0%已知$$b > 0， \operatorname{l o g}_{5} b=a， \mathrm{l g} b=c， 5^{d}=1 0$$，则下列等式一定成立的是（）
B
A.$${{d}{=}{a}{c}}$$
B.$${{a}{=}{d}{c}}$$
C.$${{c}{=}{a}{d}}$$
D.$$d=a+c$$
3、['抽象函数的应用'， '指数方程与指数不等式的解法'， '指数与对数的关系'， '函数求定义域']正确率60.0%若函数$$y=f ( x+1 )$$的定义域为$$[ 0， 1 ]$$，则$$y=f \， ( 2^{x}-2 )$$的定义域是（）
B
A.$$[ 0， 1 ]$$
B.$$[ \operatorname{l o g}_{2} 3， 2 ]$$
C.$$[ 1， \operatorname{l o g}_{2} 3 ]$$
D.$$[ 1， 2 ]$$
4、['指数型函数模型的应用'， '指数与对数的关系']正确率40.0%$${{“}}$$绿水青山就是金山银山$${{”}}$$，党的十九大以来，城乡深化河道生态环境治理，科学治污．某乡村一条污染河道的蓄水量为$${{v}}$$立方米，每天的进出水量为$${{k}}$$立方米．已知污染源以每天$${{r}}$$个单位污染河水，某一时段$${{t}}$$（单位：天）河水污染质量指数为$${{m}{(}{t}{)}}$$（每立方米河水所含的污染物）满足$$m ( t )=\frac r k+\left( m_{0}-\frac r k \right) \mathrm{e}^{-\frac{k} {v} t}$$（$${{m}_{0}}$$为初始质量指数），经测算，河道蓄水量是每天进出水量的$${{8}{0}}$$倍．若从现在开始关闭污染源，要使河水的污染水平下降到初始时的$${{1}{0}{%}}$$，需要的时间大约是（参考数据：$$\operatorname{l n} 1 0 \approx2. 3 0$$）（）
C
A.$${{1}}$$个月
B.$${{3}}$$个月
C.半年
D.$${{1}}$$年
5、['指数型函数模型的应用'， '指数与对数的关系'， '对数的运算性质']正确率40.0%某公司为激励创新，计划逐年加大研发资金投入.若该公司$${{2}{0}{1}{5}}$$年全年投入研发资金$${{1}{3}{0}}$$万元，在此基础上，每年投入的研发资金比上一年增长$${{1}{2}{%}{，}}$$则该公司全年投入的研发资金开始超过$${{2}{0}{0}}$$万元的年份是（）
(参考数据：$$\mathrm{l g} \; 1. 1 2 \approx0. 0 5， \; \mathrm{l g} \; 1. 3 \approx0. 1 1， \; \mathrm{l g} \; 2 \approx0. 3 0 )$$
B
A.$${{2}{0}{1}{8}}$$年
B.$${{2}{0}{1}{9}}$$年
C.$${{2}{0}{2}{0}}$$年
D.$${{2}{0}{2}{1}}$$年
6、['对数（型）函数的单调性'， '指数与对数的关系'， '对数的运算性质'， '一般幂函数的图象和性质']正确率40.0%已知$$\operatorname{l o g}_{2} x=\operatorname{l o g}_{3} y=\operatorname{l o g}_{5} z < 0$$，则$$\frac{2} {x} \cdot\frac{3} {y} \cdot\frac{5} {z}$$的大小排序为（）
A
A.$$\frac{2} {x} < \frac{3} {y} < \frac{5} {z}$$
B.$$\frac{3} {y} < \frac{2} {x} < \frac{5} {z}$$
C.$$\frac{5} {z} < \frac{2} {x} < \frac{3} {y}$$
D.$$\frac{5} {z} < \frac{3} {y} < \frac{2} {x}$$
7、['指数与对数的关系'， '对数的运算性质'， '对数的换底公式及其推论']正确率40.0%设$$2^{a}=5^{b}=m$$，且$$\frac{1} {a}+\frac{1} {b}=2，$$则$${{m}{=}{（}}$$）
A
A.$${\sqrt {{1}{0}}}$$
B.$${{1}{0}}$$
C.$${{2}{0}}$$
D.$${{1}{0}{0}}$$
8、['对数（型）函数过定点'， '指数与对数的关系'， '反函数的性质']正确率60.0%设函数$$y=\operatorname{l o g}_{a} ( x+b ) ( a > 0$$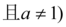
的图象过点$$( 4， 2 )$$
A
A.$${{8}}$$
B.$${{−}{2}}$$
C.$${{2}}$$
D.$${{−}{8}}$$
9、['指数与对数的关系'， '对数的运算性质']正确率80.0%若$${{l}{g}{a}}$$，$${{l}{g}{b}}$$是方程$$3 x^{2}+6 x+1=0$$的两个根，则$${{a}{b}}$$的值等于（）
C
A.$${{2}}$$
B.$$\frac{1} {2}$$
C.$$\frac{1} {1 0 0}$$
D.$${\sqrt {{1}{0}}}$$
10、['N次方根的定义与性质'， '有理数指数幂的运算性质'， '指数与对数的关系']正确率60.0%若$$\operatorname{l o g}_{x} \sqrt{y}=z$$，则（）
B
A.$${{y}^{7}{=}{{x}^{z}}}$$
B. $$y=x^{7 z}$$
C.$${{y}{=}{7}{x}}$$
D. $$y=z^{7 x}$$
1. 解析：
由 $$6^m = 2$$ 和 $$6^n = 3$$，取对数得 $$m = \log_6 2$$，$$n = \log_6 3$$。
所求表达式为 $$m^2 + n^2 + 2mn = (m + n)^2$$。
因为 $$m + n = \log_6 2 + \log_6 3 = \log_6 (2 \times 3) = \log_6 6 = 1$$，所以 $$(m + n)^2 = 1$$。
答案为 B。
2. 解析：
由 $$\log_5 b = a$$，得 $$b = 5^a$$。
由 $$\lg b = c$$，得 $$b = 10^c$$。
由 $$5^d = 10$$，得 $$d = \log_5 10$$。
将 $$b = 5^a = 10^c$$ 代入，取对数得 $$a = c \log_5 10 = c d$$。
答案为 B。
3. 解析：
函数 $$y = f(x+1)$$ 的定义域为 $$[0, 1]$$，即 $$0 \leq x \leq 1$$，所以 $$1 \leq x+1 \leq 2$$。
因此，$$f(u)$$ 的定义域为 $$1 \leq u \leq 2$$。
对于 $$y = f(2^x - 2)$$，需满足 $$1 \leq 2^x - 2 \leq 2$$，即 $$3 \leq 2^x \leq 4$$。
解得 $$\log_2 3 \leq x \leq 2$$。
答案为 B。
4. 解析：
由题意，$$v = 80k$$，污染源关闭后 $$r = 0$$，污染指数公式简化为 $$m(t) = m_0 e^{-\frac{k}{v} t}$$。
要求 $$m(t) = 0.1 m_0$$，代入得 $$0.1 = e^{-\frac{k}{80k} t}$$，即 $$0.1 = e^{-\frac{t}{80}}$$。
取自然对数得 $$\ln 0.1 = -\frac{t}{80}$$，即 $$t = 80 \ln 10 \approx 80 \times 2.3 = 184$$ 天，约 6 个月。
答案为 C。
5. 解析：
设经过 $$n$$ 年后研发资金超过 200 万元，则 $$130 \times (1.12)^n > 200$$。
取对数得 $$n \log 1.12 > \log \frac{200}{130}$$，即 $$n > \frac{\log 2 - \log 1.3}{0.05} \approx \frac{0.3 - 0.11}{0.05} = 3.8$$。
因此，$$n = 4$$ 年，即 2019 年。
答案为 B。
6. 解析：
设 $$\log_2 x = \log_3 y = \log_5 z = k < 0$$，则 $$x = 2^k$$，$$y = 3^k$$，$$z = 5^k$$。
因此，$$\frac{2}{x} = 2^{1 - k}$$，$$\frac{3}{y} = 3^{1 - k}$$，$$\frac{5}{z} = 5^{1 - k}$$。
由于 $$k < 0$$，$$1 - k > 1$$，且底数越大，值越大，故 $$\frac{2}{x} < \frac{3}{y} < \frac{5}{z}$$。
答案为 A。
7. 解析：
由 $$2^a = 5^b = m$$，取对数得 $$a = \log_2 m$$，$$b = \log_5 m$$。
代入 $$\frac{1}{a} + \frac{1}{b} = 2$$，得 $$\frac{1}{\log_2 m} + \frac{1}{\log_5 m} = 2$$。
利用换底公式，$$\log_m 2 + \log_m 5 = 2$$，即 $$\log_m (2 \times 5) = 2$$，故 $$m^2 = 10$$，$$m = \sqrt{10}$$。
答案为 A。
8. 解析：
函数 $$y = \log_a (x + b)$$ 过点 $$(4, 2)$$，代入得 $$2 = \log_a (4 + b)$$，即 $$a^2 = 4 + b$$。
题目不完整，无法进一步推导。
9. 解析：
由 $$\lg a$$ 和 $$\lg b$$ 是方程 $$3x^2 + 6x + 1 = 0$$ 的根，根据韦达定理：
$$\lg a + \lg b = -\frac{6}{3} = -2$$，即 $$\lg (ab) = -2$$，故 $$ab = 10^{-2} = \frac{1}{100}$$。
答案为 C。
10. 解析：
由 $$\log_x \sqrt{y} = z$$，得 $$\sqrt{y} = x^z$$，两边平方得 $$y = x^{2z}$$。
题目选项不匹配，可能是题目表述有误。