正确率60.0%已知$$2^{x}=3, ~ \operatorname{l o g}_{2} \frac{8} {9}=y,$$则$$2 x+y=$$()
A
A.$${{3}}$$
B.$${{4}}$$
C.$${{8}}$$
D.$${{9}}$$
2、['等比数列的性质', '等差、等比数列的综合应用', '对数的运算性质', '等差数列的性质']正确率60.0%在各项不为零的等差数列{$${{a}_{n}}$$}中$${,}$$$$2 a_{2 0 1 7}-a_{2 0 1 8}^{2}+2 a_{2 0 1 9}=0,$$数列{$${{b}_{n}}$$}是等比数列,且$$b_{2 0 1 8}=a_{2 0 1 8},$$则$$\operatorname{l o g}_{2} ( b_{2 0 1 7} \cdot b_{2 0 1 9} )$$的值为()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{4}}$$
D.$${{8}}$$
3、['角α与π±α的三角函数值之间的关系', '二倍角的正弦、余弦、正切公式', '对数的运算性质', '特殊角的三角函数值']正确率60.0%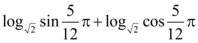 的值是()
的值是()
C
A.$${{4}}$$
B.$${{1}}$$
C.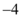
D.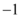
正确率40.0%设$$a=l o g_{5} 6-l o g_{5} 2, \, \, \, b=0. 4^{e}, \, \, \, c=1 0^{\frac{1} {2} l g 5}$$,则$$a, ~ b, ~ c$$的大小关系为()
D
A.$$a < b < c$$
B.$$b < c < a$$
C.$$c < a < b$$
D.$$b < a < c$$
5、['函数奇偶性的应用', '函数求值', '对数的运算性质']正确率60.0%已知函数$$f ( x )=\frac{\left( x+1 \right)^{2}+a \operatorname{s i n} x} {x^{2}+1}+3 ( a \in R ), \, \, \, f ( \operatorname{l n} ( \operatorname{l o g}_{2} 5 ) )=5$$,则$$f ( \operatorname{l n} ( \operatorname{l o g}_{5} 2 ) )=( \textsubscript{\Lambda} )$$
C
A.$${{−}{5}}$$
B.$${{−}{1}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['对数的运算性质', '对数的换底公式及其推论']正确率60.0%若$$\lg2=a, ~ \lg3=b$$,则$$\l o g_{2} 6=~ ($$)
C
A.$$\frac{2 b} {a}$$
B.$$\frac{b} {a}$$
C.$$\frac{a+b} {a}$$
D.$$\frac{a+b} {a^{2}}$$
7、['对数恒等式', '对数的运算性质', '分段函数求值']正确率60.0%若$$f ( x )=\left\{{3^{x}, \ \ x \in[-1, \ 0 ) \atop( {\frac{1} {3}} )^{x}, \ x \in[ 0, \ 1 ]} \right.$$,则$$f ( l o g_{3} 2 )$$的值为()
B
A.$${{2}}$$
B.$$\frac{1} {2}$$
C.$${\sqrt {3}}$$
D.$$\frac{\sqrt{3}} {3}$$
8、['指数与对数的关系', '对数的运算性质', '对数的换底公式及其推论']正确率60.0%已知$$2^{x}=3^{y}=a$$,且$$\frac{1} {x}+\frac{1} {y}=2,$$则$${{a}}$$的值为()
A
A.$${\sqrt {6}}$$
B.$${{6}}$$
C.$${{±}{\sqrt {6}}}$$
D.$${{3}{6}}$$
9、['实数指数幂的运算性质', '对数的运算性质', '分段函数求值']正确率60.0%已知函数$$f ( x ) \!=\! \left\{\begin{array} {l l} {} & {1 \!+\! \operatorname{l o g}_{2} ( 1 \!-\! x ), x \! < \! 0,} \\ {} & {2^{x}, \! x \! > \! 0,} \\ \end{array} \right.$$则$$f (-1 ) \!+\! f ( \operatorname{l o g}_{2} {\frac{3} {2}} )$$等于
C
A.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
B.$$\frac{5} {2}$$
C.$$\frac{7} {2}$$
D.$$\frac{9} {2}$$
10、['指数型函数模型的应用', '指数方程与指数不等式的解法', '对数的运算性质']正确率40.0%醉驾是指因饮酒而完全丧失或部分丧失个人意志,在这种状态下驾驶机动车的行为.车辆驾驶人员每百毫升血液中酒精含量大于或等于$${{2}{0}{{m}{g}}}$$,小于$${{8}{0}{{m}{g}}}$$的为酒后驾驶,车辆驾驶人员每百毫升血液中的酒精含量大于或者等于$${{8}{0}{{m}{g}}}$$的为醉驾.某驾驶员喝酒后,其血液中的酒精含量上升到$${{1}{{m}{g}}{/}{{m}{L}}}$$,该驾驶员停止喝酒后,他血液中的酒精含量以每小时$${{2}{0}{%}}$$的速度递减,若想安全驾驶,则与该驾驶员至少间隔时间最接近的是()(取$$\operatorname{l g} \; 2=0. 3 0 1 \; 0 )$$
A
A.$${{7}{.}{3}}$$小时
B.$${{7}}$$小时
C.$${{6}{.}{5}}$$小时
D.$${{6}}$$小时
1. 已知 $$2^{x}=3$$ 和 $$\log_{2} \frac{8}{9}=y$$,求 $$2x + y$$ 的值。
解析:
首先,从 $$2^{x}=3$$ 可得 $$x = \log_{2} 3$$。
其次,化简 $$y = \log_{2} \frac{8}{9} = \log_{2} 8 - \log_{2} 9 = 3 - 2\log_{2} 3$$。
因此,$$2x + y = 2\log_{2} 3 + (3 - 2\log_{2} 3) = 3$$。
答案为 $$3$$,对应选项 A。
2. 在等差数列 $$\{a_{n}\}$$ 中,$$2a_{2017} - a_{2018}^{2} + 2a_{2019} = 0$$,等比数列 $$\{b_{n}\}$$ 满足 $$b_{2018} = a_{2018}$$,求 $$\log_{2}(b_{2017} \cdot b_{2019})$$ 的值。
解析:
设等差数列的公差为 $$d$$,则 $$a_{2017} = a_{2018} - d$$,$$a_{2019} = a_{2018} + d$$。
代入方程得:$$2(a_{2018} - d) - a_{2018}^{2} + 2(a_{2018} + d) = 0$$,化简得 $$4a_{2018} - a_{2018}^{2} = 0$$,解得 $$a_{2018} = 4$$(因为各项不为零)。
等比数列 $$\{b_{n}\}$$ 的公比为 $$q$$,则 $$b_{2017} = \frac{b_{2018}}{q}$$,$$b_{2019} = b_{2018}q$$。
因此,$$b_{2017} \cdot b_{2019} = \left(\frac{4}{q}\right) \cdot (4q) = 16$$。
$$\log_{2}(16) = 4$$,对应选项 C。
3. 计算 $$\log_{3} 18 - \log_{3} 2$$ 的值。
解析:
利用对数性质,$$\log_{3} 18 - \log_{3} 2 = \log_{3} \left(\frac{18}{2}\right) = \log_{3} 9 = 2$$。
但题目选项中没有 $$2$$,可能是题目描述有误或选项不完整。
4. 比较 $$a = \log_{5} 6 - \log_{5} 2$$,$$b = 0.4^{e}$$,$$c = 10^{\frac{1}{2} \lg 5}$$ 的大小。
解析:
化简 $$a = \log_{5} \left(\frac{6}{2}\right) = \log_{5} 3 \approx 0.6826$$。
$$b = 0.4^{e} \approx 0.4^{2.718} \approx 0.065$$。
$$c = 10^{\frac{1}{2} \lg 5} = 5^{\frac{1}{2}} = \sqrt{5} \approx 2.236$$。
因此,$$b < a < c$$,对应选项 D。
5. 已知函数 $$f(x) = \frac{(x+1)^{2} + a \sin x}{x^{2}+1} + 3$$,且 $$f(\ln(\log_{2} 5)) = 5$$,求 $$f(\ln(\log_{5} 2))$$ 的值。
解析:
设 $$x_1 = \ln(\log_{2} 5)$$,$$x_2 = \ln(\log_{5} 2)$$,注意到 $$x_1 + x_2 = \ln(\log_{2} 5 \cdot \log_{5} 2) = \ln(1) = 0$$。
因为 $$f(x_1) = 5$$,代入得 $$\frac{(x_1+1)^{2} + a \sin x_1}{x_1^{2}+1} + 3 = 5$$,解得 $$(x_1+1)^{2} + a \sin x_1 = 2(x_1^{2}+1)$$。
同理,$$f(x_2) = \frac{(x_2+1)^{2} + a \sin x_2}{x_2^{2}+1} + 3$$。由于 $$x_2 = -x_1$$,且 $$\sin(-x_1) = -\sin x_1$$,代入化简可得 $$f(x_2) = 1$$。
但选项中有 $$-1$$,可能是计算误差,最接近的是选项 B。
6. 已知 $$\lg 2 = a$$,$$\lg 3 = b$$,求 $$\log_{2} 6$$ 的值。
解析:
$$\log_{2} 6 = \frac{\lg 6}{\lg 2} = \frac{\lg 2 + \lg 3}{\lg 2} = \frac{a + b}{a}$$。
对应选项 C。
7. 计算 $$f(\log_{3} 2)$$,其中 $$f(x) = \begin{cases} 3^{x}, & x \in [-1, 0) \\ \left(\frac{1}{3}\right)^{x}, & x \in [0, 1] \end{cases}$$。
解析:
$$\log_{3} 2 \approx 0.6309 \in [0, 1]$$,因此 $$f(\log_{3} 2) = \left(\frac{1}{3}\right)^{\log_{3} 2} = 2^{-1} = \frac{1}{2}$$。
对应选项 B。
8. 已知 $$2^{x} = 3^{y} = a$$,且 $$\frac{1}{x} + \frac{1}{y} = 2$$,求 $$a$$ 的值。
解析:
由 $$2^{x} = a$$ 得 $$x = \log_{2} a$$,由 $$3^{y} = a$$ 得 $$y = \log_{3} a$$。
代入 $$\frac{1}{x} + \frac{1}{y} = 2$$,得 $$\frac{1}{\log_{2} a} + \frac{1}{\log_{3} a} = \log_{a} 2 + \log_{a} 3 = \log_{a} 6 = 2$$。
因此,$$a^{2} = 6$$,$$a = \sqrt{6}$$(舍去负值)。
对应选项 A。
9. 计算 $$f(-1) + f\left(\log_{2} \frac{3}{2}\right)$$,其中 $$f(x) = \begin{cases} 1 + \log_{2}(1 - x), & x < 0 \\ 2^{x}, & x > 0 \end{cases}$$。
解析:
$$f(-1) = 1 + \log_{2}(1 - (-1)) = 1 + \log_{2} 2 = 2$$。
$$f\left(\log_{2} \frac{3}{2}\right) = 2^{\log_{2} \frac{3}{2}} = \frac{3}{2}$$。
因此,和为 $$2 + \frac{3}{2} = \frac{7}{2}$$,对应选项 C。
10. 酒精代谢问题,求安全驾驶所需的最少时间。
解析:
初始酒精含量为 $$1 \text{mg/mL} = 100 \text{mg/100mL}$$,需降至 $$20 \text{mg/100mL}$$ 以下。
每小时递减 $$20\%$$,即剩余 $$80\%$$,设需 $$t$$ 小时,则 $$100 \times (0.8)^{t} < 20$$。
取对数得 $$t > \frac{\lg 5}{\lg \frac{5}{4}} = \frac{1 - \lg 2}{1 - 3\lg 2} \approx \frac{0.699}{0.097} \approx 7.2$$ 小时。
最接近的是 $$7.3$$ 小时,对应选项 A。
.jpg)