正确率60.0%已知$$f ( x )=\operatorname{l o g}_{a} x ( a > 0, \; a \neq1 ),$$若函数$$y=f ( x )$$的图像经过点$$( 4, \ 2 ),$$则$$f ( 2 \sqrt{2} )=$$()
C
A.$${{2}}$$
B.$${{2}{\sqrt {2}}}$$
C.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
2、['同角三角函数的商数关系', '两角和与差的正弦公式', '对数恒等式']正确率60.0%已知$$\operatorname{s i n} ( \alpha+\beta)=\frac{1} {2}, \operatorname{s i n} ( \alpha-\beta)=\frac{1} {3},$$则$$\operatorname{l o g}_{\sqrt{5}} \left( \frac{\zeta\mathrm{t a n} \; \alpha} {\zeta\mathrm{t a n} \; \beta} \right)^{2}$$等于$${{(}{)}}$$
C
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
3、['等比数列的性质', '对数恒等式', '对数的运算性质']正确率60.0%己知等比数列$${{\{}{{a}_{n}}{\}}}$$的各项均为正数,若$$a_{1 0 0 8} a_{1 0 1 1}+a_{1 0 0 9} a_{1 0 1 0}=6$$,则$$\operatorname{l o g}_{3} a_{1}+\operatorname{l o g}_{3} a_{2}+\operatorname{l o g}_{3} a_{3}+\cdots+\operatorname{l o g}_{3} a_{2 0 1 8}=$$
A
A.$${{1}{0}{0}{9}}$$
B.$${{1}{0}{1}{0}}$$
C.$${{2}{0}{1}{8}}$$
D.$${{2}{0}{2}{0}}$$
4、['函数中的存在性问题', '指数与对数的关系', '已知函数值(值域)求自变量或参数', '不等式的解集与不等式组的解集', '对数恒等式']正确率19.999999999999996%设$${{a}{>}{1}}$$,若仅有一个常数$${{c}}$$使得对于任意的$$x \in[ a, a^{3} ]$$,都有$$y \in[ 1+\operatorname{l o g}_{a} 2-a^{3}, 2-a ]$$满足方程$$a^{x} a^{y}=c$$,则$${{a}}$$的取值集合为$${{(}{)}}$$
C
A.$${{\{}{4}{\}}}$$
B.$$\{\frac{3} {2}, 2 \}$$
C.$${{\{}{2}{\}}}$$
D.$$\{\frac{3} {2} \}$$
5、['函数图象的识别', '对数的性质', '对数恒等式', '分段函数的图象']正确率60.0%函数$${{y}{=}{3}{{|}{{l}{o}{g}_{3}}{x}{|}}}$$的图象是()
A
A.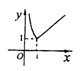
B.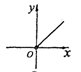
C.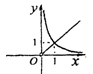
D.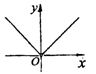
正确率60.0%下列计算错误的是()
D
A.$$\sqrt{2} \cdot\sqrt{2}=2^{\frac{2} {3}}$$
B.$$(-2 7 )^{\frac{1} {3}}=-3$$
C.$$2^{l o g_{2} 5}=5$$
D.$$\l g 2 \cdot\l g 5=1$$
7、['抽象函数的应用', '对数恒等式', '函数单调性与奇偶性综合应用']正确率40.0%已知函数$${{f}{(}{x}{)}}$$是定义在$${{R}}$$上的奇函数,且在$$[ 0, \ \ +\infty)$$上是增函数,若实数$${{a}}$$满足$$3 f ~ ( l o g_{2} a ) ~+f ~ ( ~-l o g_{2} a ) ~ \gg2 f ~ ( 1 )$$,则实数$${{a}}$$的取值范围是()
C
A.$$( \ 0, \ 2 ]$$
B.$$(-\infty, \ 2 ]$$
C.$$[ 2, ~+\infty)$$
D.$$[ 1, ~+\infty)$$
8、['对数恒等式', '分段函数求值']正确率80.0%若函数$$f ( x )=\left\{\begin{aligned} {} & {{} ( \frac{1} {4} )^{x}, x \in[-1, 0 )} \\ {} & {{} 4^{x}, x \in[ 0, 1 ]} \\ \end{aligned} \right.$$则$$f ( \operatorname{l o g}_{4} 3 )=( \textsubscript{\Lambda} )$$
B
A.$$\frac{1} {3}$$
B.$${{3}}$$
C.$$\frac{1} {4}$$
D.$${{4}}$$
9、['对数恒等式', '分段函数求值']正确率60.0%已知$$f ( x )=\left\{\begin{array} {l l} {2^{x}, x < 1} \\ {f ( x-1 ), x \geq1} \\ \end{array} \right.$$,则$$f ( l o g_{2} 8 ) ~=~ ($$)
C
A.$${{8}}$$
B.$${{4}}$$
C.$${{1}}$$
D.$${{0}}$$
10、['已知函数值(值域)求自变量或参数', '对数恒等式', '分段函数求值']正确率60.0%设$$f ( x )=\left\{\begin{matrix} {\operatorname{l o g}_{2} ( x^{2}+t ), x < 0} \\ {3 \left( t-1 \right)^{x}, x \geq0} \\ \end{matrix} \right.$$,且$$f ( \frac{1} {2} )=6$$,则$$f ( f (-2 ) )$$的值为$${{(}{)}}$$
B
A.$${{2}{7}}$$
B.$${{2}{4}{3}}$$
C.$$\frac{1} {2 7}$$
D.$$\frac{1} {2 4 3}$$
1. 由题意,函数 $$y = f(x) = \log_a x$$ 经过点 $$(4, 2)$$,代入得:$$2 = \log_a 4$$,解得 $$a = 2$$。因此,$$f(2\sqrt{2}) = \log_2 (2\sqrt{2}) = \log_2 2 + \log_2 2^{1/2} = 1 + \frac{1}{2} = \frac{3}{2}$$。答案为 $$C$$。
2. 利用正弦和差公式:$$\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta = \frac{1}{2}$$,$$\sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta = \frac{1}{3}$$。解得 $$\sin \alpha \cos \beta = \frac{5}{12}$$,$$\cos \alpha \sin \beta = \frac{1}{12}$$。因此,$$\frac{\tan \alpha}{\tan \beta} = \frac{\sin \alpha \cos \beta}{\cos \alpha \sin \beta} = 5$$。所求表达式为 $$\log_{\sqrt{5}} \left(5\right)^2 = \log_{\sqrt{5}} 25 = 4$$。答案为 $$C$$。
3. 设等比数列的公比为 $$q$$,则 $$a_{1008} a_{1011} = a_{1009} a_{1010} = a_1^2 q^{2017}$$。由题意得 $$2a_1^2 q^{2017} = 6$$,即 $$a_1^2 q^{2017} = 3$$。所求和为 $$\log_3 (a_1 a_2 \cdots a_{2018}) = \log_3 \left(a_1^{2018} q^{\frac{2017 \times 2018}{2}}\right) = 2018 \log_3 a_1 + \frac{2017 \times 2018}{2} \log_3 q$$。注意到 $$a_1^2 q^{2017} = 3$$,故 $$\log_3 a_1 + \frac{2017}{2} \log_3 q = \frac{1}{2}$$。因此,和为 $$2018 \times \frac{1}{2} = 1009$$。答案为 $$A$$。
4. 方程 $$a^x a^y = c$$ 可化为 $$y = \log_a c - x$$。由题意,对于 $$x \in [a, a^3]$$,$$y$$ 需满足 $$1 + \log_a 2 - a^3 \leq y \leq 2 - a$$。因此,$$\log_a c - a^3 \geq 1 + \log_a 2 - a^3$$ 且 $$\log_a c - a \leq 2 - a$$,即 $$\log_a c \geq 1 + \log_a 2$$ 且 $$\log_a c \leq 2$$。解得 $$c = 2a$$ 且 $$c = a^2$$,故 $$2a = a^2$$,解得 $$a = 2$$($$a > 1$$)。答案为 $$C$$。
5. 函数 $$y = 3^{|\log_3 x|}$$ 可以化简为 $$y = x$$ 当 $$x \geq 1$$,$$y = \frac{1}{x}$$ 当 $$0 < x < 1$$。图像在 $$x=1$$ 处连续且通过点 $$(1,1)$$,符合选项 $$C$$ 的特征。答案为 $$C$$。
6. 选项 $$D$$ 错误,因为 $$\lg 2 \cdot \lg 5 \neq 1$$(实际约为 $$0.3010 \times 0.6990 \approx 0.210$$)。其他选项均正确:$$A$$ 中 $$\sqrt{2} \cdot \sqrt{2} = 2 = 2^{2/2}$$;$$B$$ 中 $$(-27)^{1/3} = -3$$;$$C$$ 中 $$2^{\log_2 5} = 5$$。答案为 $$D$$。
7. 由奇函数性质,$$f(-\log_2 a) = -f(\log_2 a)$$。不等式化为 $$2f(\log_2 a) \geq 2f(1)$$,即 $$f(\log_2 a) \geq f(1)$$。由于 $$f$$ 在 $$[0, +\infty)$$ 上增函数,故 $$\log_2 a \geq 1$$,解得 $$a \geq 2$$。答案为 $$C$$。
8. 首先计算 $$\log_4 3$$,注意到 $$0 = \log_4 1 < \log_4 3 < \log_4 4 = 1$$,因此 $$f(\log_4 3) = 4^{\log_4 3} = 3$$。答案为 $$B$$。
9. 由于 $$\log_2 8 = 3 \geq 1$$,递归计算得 $$f(3) = f(2) = f(1) = f(0) = 2^0 = 1$$。答案为 $$C$$。
10. 由 $$f\left(\frac{1}{2}\right) = 3(t-1)^{1/2} = 6$$,解得 $$t = 5$$。因此,$$f(-2) = \log_2 (4 + 5) = \log_2 9$$,$$f(f(-2)) = 3 \times 4^{\log_2 9} = 3 \times 2^{2 \log_2 9} = 3 \times 9^2 = 243$$。答案为 $$B$$。
.jpg)