.jpg)
正确率60.0%已知函数$$f ( x )=\operatorname{l o g}_{a} ( x-1 )-3 ( a > 0$$，且$${{a}{≠}{1}{)}}$$的图象恒过定点$${{P}}$$.若角$${{α}}$$的顶点与原点重合， 始边与$${{x}}$$轴的正半轴重合，终边经过点$${{P}}$$，则$${{s}{i}{n}{α}}$$的值为$${{(}{)}}$$．
D
A.$$\frac{\sqrt{1 0}} {1 0}$$
B.$$- \frac{3 \sqrt{1 0}} {1 0}$$
C.$$\frac{\sqrt{1 3}} {1 3}$$
D.$$- \frac{3 \sqrt{1 3}} {1 3}$$
2、['对数（型）函数过定点']正确率60.0%函数$$y=1-\operatorname{l o g}_{a} ( 1-x )$$的图像恒过定点（）
D
A.$$( 1， 0 )$$
B.$$\left( 1， 1 \right)$$
C.$$( 0， 0 )$$
D.$$( 0， 1 )$$
3、['对数（型）函数过定点'， '正弦（型）函数的单调性'， '对数（型）函数的定义域'， '对数（型）函数的值域'， '对数（型）函数的单调性'， '正弦（型）函数的周期性'， '正弦（型）函数的定义域和值域'， '常见函数的零点'， '函数零点的概念'， '对数函数的定义'， '函数零点个数的判定']正确率60.0%函数$$f ( x )=| \operatorname{l g} x |-\operatorname{s i n} x |$$的零点个数为$${{(}{)}}$$
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['对数（型）函数过定点'， '利用基本不等式求最值']正确率40.0%函数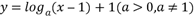
，图象恒过定点$${{A}}$$
C
A.$${{6}}$$
B.$${{7}}$$
C.$${{8}}$$
D.$${{9}}$$
5、['对数（型）函数过定点'， '基本不等式：(√ab)≤(a+b)/2，当且仅当a=b时等号成立'， '对数（型）函数的单调性'， '对数的运算性质'， '对数函数的定义'， '函数零点的值或范围问题']正确率40.0%已知函数$${{f}{{(}{x}{)}}{=}{{|}{{l}{g}}{x}{|}}}$$.若$${{a}{≠}{b}}$$且，$$f \left( a \right)=f \left( b \right)$$，则$${{a}{+}{b}}$$的取值范围是（）
C
A.$$( 1，+\infty)$$
B.$$[ 1，+\infty)$$
C.$$( 2，+\infty)$$
D.$$[ 2，+\infty)$$
6、['对数（型）函数过定点'， '对数的运算性质'， '幂函数的定义']正确率60.0%已知函数$$y=l o g_{a} \， \， ( \， x-1 ) \， \， \，+4 \， \， ( \， a > 0$$且$${{a}{≠}{1}{）}}$$的图象恒过定点$${{P}}$$，点$${{P}}$$在幂函数$$y=f ~ ( x )$$的图象上，则$$\lg f ~ ( \mathrm{\bf~ 2} ) ~+\l g f ~ ( \mathrm{\bf~ 5} ) ~=~ ( \mathrm{\bf~$$）
B
A.$${{−}{2}}$$
B.$${{2}}$$
C.$${{−}{1}}$$
D.$${{1}}$$
7、['对数（型）函数过定点']正确率60.0%函数$$y=\operatorname{l o g}_{a} \left( x+2 \right)+1 \left( a > 0 \ss a \neq1 \right)$$的图象过定点（）
D
A.$$( 1， 2 )$$
B.$$( 2， 1 )$$
C.$$(-2， 1 )$$
D.$$(-1， 1 )$$
8、['对数（型）函数过定点'， '对数（型）函数的单调性']正确率60.0%函数$$y=\operatorname{l o g}_{a} {( 2 x-1 )}+3$$的图象必过点（）
B
A.$$( \frac{1} {2}， 4 )$$
B.$$( 1， 3 )$$
C.$$( \frac{1} {2}， 3 )$$
D.$$( 1， 4 )$$
9、['对数（型）函数过定点']正确率60.0%若函数$$y=\operatorname{l o g}_{a} ( x+3 ) ( a > 0$$，且$${{a}{≠}{1}{)}}$$的图象恒过定点$${{P}}$$，则点$${{P}}$$的坐标是
A
A.$$(-2， 0 )$$
B.$$( 0， 2 )$$
C.$$( 0， 3 )$$
D.$$(-3， 0 )$$
10、['对数（型）函数过定点']正确率60.0%函数$$f \left( x \right)=\operatorname{l o g}_{a} \left( x+1 \right)-3$$的图象恒过的定点是（）
A
A.$$( 0，-3 )$$
B.$$( 0，-2 )$$
C.$$( 1， 0 )$$
D.$$( 0， 0 )$$
1. 函数 $$f(x) = \log_a (x-1) - 3$$ 的图象恒过定点 $$P$$。对数函数 $$\log_a (x-1)$$ 在 $$x-1 = 1$$ 时值为 0，即 $$x = 2$$，此时 $$f(2) = -3$$，故 $$P(2, -3)$$。角 $$\alpha$$ 的终边经过 $$P$$，则 $$\sin \alpha = \frac{y}{\sqrt{x^2 + y^2}} = \frac{-3}{\sqrt{2^2 + (-3)^2}} = -\frac{3\sqrt{13}}{13}$$。正确答案为 D。
2. 函数 $$y = 1 - \log_a (1-x)$$ 的图象恒过定点需满足 $$1-x = 1$$，即 $$x = 0$$，此时 $$y = 1 - 0 = 1$$，故定点为 $$(0, 1)$$。正确答案为 D。
3. 函数 $$f(x) = |\lg x| - |\sin x|$$ 的零点即 $$|\lg x| = |\sin x|$$。分析区间 $$(0, 1]$$ 和 $$(1, +\infty)$$，结合图像可知有两个交点。正确答案为 B。
4. 题目描述不完整，无法解析。
5. 函数 $$f(x) = |\lg x|$$，若 $$a \neq b$$ 且 $$f(a) = f(b)$$，则 $$\lg a = -\lg b$$，即 $$ab = 1$$。故 $$a + b = a + \frac{1}{a} > 2$$（当 $$a \neq 1$$ 时）。正确答案为 C。
6. 函数 $$y = \log_a (x-1) + 4$$ 的图象恒过定点 $$P(2, 4)$$。设幂函数 $$f(x) = x^k$$，由 $$f(2) = 2^k = 4$$ 得 $$k = 2$$，故 $$f(x) = x^2$$。则 $$\lg f(2) + \lg f(5) = \lg 4 + \lg 25 = \lg 100 = 2$$。正确答案为 B。
7. 函数 $$y = \log_a (x+2) + 1$$ 的图象恒过定点需满足 $$x+2 = 1$$，即 $$x = -1$$，此时 $$y = 0 + 1 = 1$$，故定点为 $$(-1, 1)$$。正确答案为 D。
8. 函数 $$y = \log_a (2x-1) + 3$$ 的图象恒过定点需满足 $$2x-1 = 1$$，即 $$x = 1$$，此时 $$y = 0 + 3 = 3$$，故定点为 $$(1, 3)$$。正确答案为 B。
9. 函数 $$y = \log_a (x+3)$$ 的图象恒过定点需满足 $$x+3 = 1$$，即 $$x = -2$$，此时 $$y = 0$$，故定点为 $$(-2, 0)$$。正确答案为 A。
10. 函数 $$f(x) = \log_a (x+1) - 3$$ 的图象恒过定点需满足 $$x+1 = 1$$，即 $$x = 0$$，此时 $$f(0) = -3$$，故定点为 $$(0, -3)$$。正确答案为 A。