正确率40.0%已知函数$$f ( x )=| \operatorname{l o g}_{2} ( x+1 ) |,$$若$$f ( m )=f ( n ), \, \, m \neq n,$$则$$\frac{1} {m}+\frac{1} {n}$$等于()
B
A.$${{1}}$$
B.$${{−}{1}}$$
C.$${{0}}$$
D.$${{2}}$$
2、['对数函数y= log2 X的图象和性质', '对数(型)函数的定义域', '对数(型)函数的值域']正确率80.0%函数$${{y}{=}{{l}{o}{g}_{2}}{x}}$$的定义域是$$[ 1, 6 4 ),$$则其值域是()
C
A.$${{R}}$$
B.$$[ 0, ~+\infty)$$
C.$$[ 0, 6 )$$
D.$$[ 0, 6 4 )$$
3、['利用函数单调性解不等式', '对数函数y= log2 X的图象和性质', '函数单调性的判断']正确率60.0%已知函数$$f ( x )=\frac2 x-\operatorname{l o g}_{2} x,$$则不等式$$f ( x ) > 0$$的解集是()
D
A.$$( 0, \ 1 )$$
B.$$(-\infty, \; 2 )$$
C.$$( 2, ~+\infty)$$
D.$$( 0, \ 2 )$$
4、['对数函数y= log2 X的图象和性质', '二次函数的零点及其与对应方程的根、不等式解集之间的关系']正确率60.0%函数$$y=\operatorname{l o g}_{2} x-\sqrt{x}$$的图象大致是()
A
A.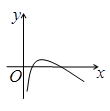
B.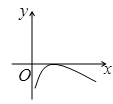
C.
D.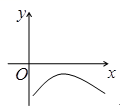
正确率40.0%方程$$\operatorname{s i n} x=\operatorname{l g} | x |$$根的个数为()
C
A.$${{4}}$$个
B.$${{5}}$$个
C.$${{6}}$$个
D.$${{8}}$$个
6、['对数函数y= log2 X的图象和性质', '函数的最大(小)值', '二次函数的零点及其与对应方程的根、不等式解集之间的关系', '对数的运算性质']正确率19.999999999999996%设正数$${{x}{,}{y}}$$满足$$l o g_{\frac{1} {3}} x+l o g_{3} y=m ~ ( ~ m \in[-1, ~ 1 ] )$$,若不等式$$3 a x^{2}-1 8 x y+\begin{array} {c} {( 2 a+3 )} \\ {y^{2} \geqslant\ ( x-y )} \\ \end{array}^{2}$$有解,则实数$${{a}}$$的取值范围是()
C
A.$$( 1, ~ \frac{5 5} {2 9} ]$$
B.$$( 1, ~ \frac{3 1} {2 1} ]$$
C.$$[ \frac{3 1} {2 1}, ~+\infty)$$
D.$$[ \frac{5 5} {2 9}, ~ ~+\infty)$$
7、['在给定区间上恒成立问题', '对数函数y= log2 X的图象和性质', '对数方程与对数不等式的解法', '对数的运算性质', '给定参数范围的恒成立问题', '二次函数的图象分析与判断']正确率40.0%若不等式$$t^{2}-\operatorname{l o g}_{2 x} t < 0$$对任意$$t \in( 0, \frac{1} {2} ]$$恒成立,则实数$${{x}}$$的取值范围是()
A
A.$$\frac{1} {3 2} < \! x < \frac{1} {2}$$
B.$$\frac{1} {6 4} \! < \! x \! < \! \frac{1} {2}$$
C.$$\frac{1} {1 2 8} < \! x < \frac{1} {2}$$
D.$$\frac{1} {1 6} < \! x < \frac{1} {2}$$
8、['对数函数y= log2 X的图象和性质', '函数图象的平移变换', '函数图象的翻折变换', '函数零点个数的判定', '分段函数的图象']正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right) \ =\left\{\begin{matrix} {| \operatorname{l o g}_{2} x |, x > 0} \\ {| x+2 |-1, x \leqslant0} \\ \end{matrix} \right.$$,若函数$$y=f ~^{(} x ) ~^{-} m+1$$有四个零点,零点从小到大依次为$$a, ~ b, ~ c, ~ d$$,则$$a+b+c d$$的值为()
C
A.$${{2}}$$
B.$${{−}{2}}$$
C.$${{−}{3}}$$
D.$${{3}}$$
9、['对数函数y= log2 X的图象和性质', '指数函数的定义', '分段函数求值']正确率60.0%已知函数$$f ( x )=\left\{\begin{array} {l l} {l o g_{2} x, x > 1} \\ {3^{x}, x \leq1} \\ \end{array} \right.$$,则$$f ( 1 )+f ( 2 )=( ~ ~ )$$
B
A.$${{1}}$$
B.$${{4}}$$
C.$${{9}}$$
D.$${{1}{2}}$$
10、['对数函数y= log2 X的图象和性质', '分段函数求值']正确率60.0%设函数$$f^{\left( \begin{matrix} {x} \\ \end{matrix} \right)}=\left\{\begin{matrix} {l n | x |, x \leq-1} \\ {e^{x}, x >-1} \\ \end{matrix} \right.$$,则)
D
A.$$\frac{1} {2}$$
B.$$\frac{1} {e}$$
C.$$\frac{2} {e}$$
D.$${{2}}$$
1. 解析:由 $$f(m) = f(n)$$ 得 $$|\log_2 (m+1)| = |\log_2 (n+1)|$$,即 $$\log_2 (m+1) = \pm \log_2 (n+1)$$。若 $$\log_2 (m+1) = \log_2 (n+1)$$,则 $$m = n$$,与题意矛盾。故 $$\log_2 (m+1) = -\log_2 (n+1)$$,即 $$(m+1)(n+1) = 1$$。展开得 $$mn + m + n = 0$$,因此 $$\frac{1}{m} + \frac{1}{n} = \frac{m+n}{mn} = -1$$。答案为 $$B$$。
3. 解析:不等式 $$f(x) > 0$$ 即 $$\frac{2}{x} - \log_2 x > 0$$。设 $$g(x) = \frac{2}{x} - \log_2 x$$,求导得 $$g'(x) = -\frac{2}{x^2} - \frac{1}{x \ln 2} < 0$$,故 $$g(x)$$ 单调递减。又 $$g(1) = 2 > 0$$,$$g(2) = 1 - 1 = 0$$,因此解集为 $$(0, 2)$$。答案为 $$D$$。
5. 解析:方程 $$\sin x = \lg |x|$$ 的根个数可通过图像法分析。$$\sin x$$ 周期为 $$2\pi$$,振幅为 1,而 $$\lg |x|$$ 在 $$|x| \geq 1$$ 时定义,且单调递增。在 $$x > 0$$ 时,两图像在 $$(0, \pi)$$ 和 $$(2\pi, 3\pi)$$ 各有一个交点;由对称性,$$x < 0$$ 时也有两个交点。此外,$$x = 0$$ 无定义。故总共有 6 个根。答案为 $$C$$。
7. 解析:不等式 $$t^2 < \log_{2x} t$$ 对 $$t \in (0, \frac{1}{2}]$$ 恒成立。当 $$2x > 1$$ 时,$$\log_{2x} t$$ 单调减,需 $$t^2 < \log_{2x} \frac{1}{2}$$ 对所有 $$t \in (0, \frac{1}{2}]$$ 成立,即 $$\frac{1}{4} \leq \log_{2x} \frac{1}{2}$$,解得 $$x \leq \frac{1}{2}$$。当 $$0 < 2x < 1$$ 时,$$\log_{2x} t$$ 单调增,需 $$t^2 < \log_{2x} t$$ 对所有 $$t \in (0, \frac{1}{2}]$$ 成立,取 $$t = \frac{1}{2}$$ 得 $$\frac{1}{4} < \log_{2x} \frac{1}{2}$$,即 $$x > \frac{1}{32}$$。综上,$$x \in (\frac{1}{32}, \frac{1}{2})$$。答案为 $$A$$。
9. 解析:根据函数定义,$$f(1) = 3^1 = 3$$,$$f(2) = \log_2 2 = 1$$,因此 $$f(1) + f(2) = 4$$。答案为 $$B$$。
.jpg)