.jpg)
正确率60.0%设点集$${{M}{=}}$$$${{\{}}$$$${{P}{|}{P}}$$是指数函数与幂函数图像的公共点或对数函数与幂函数图像的公共点$${{\}}}$$，则下列选项中的点可能是集合$${{M}}$$中的元素的是（）
D
A.$$\left( 1， \frac{1} {2} \right)$$
B.$$\left( 1，-\frac{1} {2} \right)$$
C.$$\left(-2，-\frac{1} {4} \right)$$
D.$$\left(-2， \frac{1} {4} \right)$$
2、['对数函数的定义']正确率80.0%下列函数是对数函数的是（）
D
A.$$y=\operatorname{l o g}_{a} ( 2 x )$$
B.$${{y}{=}{{l}{g}}{{1}{0}^{x}}}$$
C.$$y=\operatorname{l o g}_{a} ( x^{2}+x )$$
D.$${{y}{=}{{l}{n}}{x}}$$
3、['对数函数的定义']正确率80.0%若函数$$f ( x )=\operatorname{l g} ( a x^{2}-2 x+a )$$的定义域为$${{R}{，}}$$则实数$${{a}}$$的取值范围为（）
D
A.$$(-1， \ 0 )$$
B.$$[-1， ~ 1 ]$$
C.$$( 0， \ 1 )$$
D.$$( 1， ~+\infty)$$
4、['对数函数的定义']正确率80.0%下列函数是对数函数的是（）
B
A.$${{y}{=}{{l}{o}{g}_{2}}{{x}^{2}}}$$
B.$$y=\operatorname{l o g}_{( \pi-\mathrm{e} )} x$$
C.$$y=\operatorname{l o g}_{x} 2 ( x > 0，$$且$${{x}{≠}{1}{)}}$$
D.$$y=\operatorname{l o g}_{2} {\frac{x} {2}}$$
5、['对数函数y= log2 X的图象和性质'， '对数（型）函数的单调性'， '对数函数的定义']正确率60.0%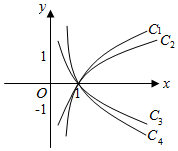
如图所示的曲线$$C_{1}， ~ C_{2}， ~ C_{3}， ~ C_{4}$$
B
A.$$d < c < b < a$$
B.$$c < d < a < b$$
C.$$b < a < c < d$$
D.$$c < d < b < a$$
6、['有理数指数幂的运算性质'， '指数与对数的关系'， '对数的运算性质'， '对数函数的定义'， '对数的换底公式及其推论']正确率40.0%已知$$2^{x}=3^{y}=5^{z}$$，且$$x， ~ y， ~ z$$均为正数，则$$2 x， ~ 3 y， ~ 5 z$$的大小关系为（）
B
A.$$2 x < 3 y < 5 z$$
B.$$3 y < 2 x < 5 z$$
C.$$5 z < 3 y < 2 x$$
D.$$5 z < 2 x < 3 y$$
7、['对数（型）函数过定点'， '基本不等式：(√ab)≤(a+b)/2，当且仅当a=b时等号成立'， '对数（型）函数的单调性'， '对数的运算性质'， '对数函数的定义'， '函数零点的值或范围问题']正确率40.0%已知函数$${{f}{{(}{x}{)}}{=}{{|}{{l}{g}}{x}{|}}}$$.若$${{a}{≠}{b}}$$且，$$f \left( a \right)=f \left( b \right)$$，则$${{a}{+}{b}}$$的取值范围是（）
C
A.$$( 1，+\infty)$$
B.$$[ 1，+\infty)$$
C.$$( 2，+\infty)$$
D.$$[ 2，+\infty)$$
8、['指数函数的定义'， '不等式比较大小'， '对数函数的定义']正确率60.0%若$$a=3. 3^{0. 3}， \ b=0. 7^{0. 7}， \ c=\mathrm{l g} \ 0. 6$$，则实数$$a， ~ b， ~ c$$的大小关系为（）
A
A.$$a > b > c$$
B.$$a > c > b$$
C.$$b > c > a$$
D.$$b > a > c$$
9、['交集'， '一元二次不等式的解法'， '对数函数的定义']正确率60.0%设$$A=\{x | x^{2}-x-6 < 0 \}， \， \， \， B=\{x | y=1 n x \}$$，则$${{A}{∩}{B}{=}}$$
D
A.$$(-1， 0 )$$
B.$$( 0， 6 )$$
C.$$(-2， 3 )$$
D.$$( 0， 3 )$$
10、['对数（型）函数过定点'， '对数（型）函数的定义域'， '对数（型）函数的值域'， '单调性的定义与证明'， '对数（型）函数的单调性'， '函数单调性的判断'， '函数的单调区间'， '对数函数的定义']正确率19.999999999999996%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=l n \left( \begin{matrix} {\epsilon-x^{2}-2 x+3} \\ \end{matrix} \right)$$，则$${{f}{（}{x}{）}}$$的增区间为（）
B
A.$${{(}{{−}{∞}{，}{−}}{1}{)}}$$
B.$$(-3，-1 )$$
C.$$[-1，+\infty)$$
D.$$[-1， 1 )$$
1. 解析：集合$$M$$包含指数函数与幂函数或对数函数与幂函数图像的公共点。对于选项A，$$(1, \frac{1}{2})$$可能满足$$y = a^x$$与$$y = x^b$$在$$x=1$$时$$a = \frac{1}{2}$$，或$$y = \log_a x$$与$$y = x^b$$在$$x=1$$时$$0 = 1$$（不成立），故A可能正确。其他选项不满足条件。
3. 解析：函数$$f(x) = \lg(ax^2 - 2x + a)$$的定义域为$$R$$，需满足$$ax^2 - 2x + a > 0$$对所有$$x \in R$$成立。因此：
- 当$$a > 0$$时，判别式$$\Delta = 4 - 4a^2 < 0$$，解得$$a > 1$$。
综合得$$a \in (1, +\infty)$$，故选D。
5. 解析：图中曲线$$C_1, C_2, C_3, C_4$$分别对应不同底数的对数函数，增长速率与底数大小相关。观察图像斜率可得$$c < d < b < a$$，故选D。
7. 解析：函数$$f(x) = |\lg x|$$，若$$f(a) = f(b)$$且$$a \neq b$$，则$$\lg a = -\lg b$$，即$$ab = 1$$。$$a + b = a + \frac{1}{a} > 2$$（$$a \neq 1$$），故选C。
9. 解析：集合$$A = \{x | x^2 - x - 6 < 0\} = (-2, 3)$$，集合$$B = \{x | y = \ln x\} = (0, +\infty)$$，故$$A \cap B = (0, 3)$$，选D。