正确率60.0%设$${{a}{,}{b}}$$都是不等于$${{1}}$$的正数,则$${{“}}$$ $${{”}}$$
$${{”}}$$
A
A.充分不必要
B.必要不充分
C.充要
D.既不充分也不必要
2、['对数型复合函数的应用', '底数对对数函数图象的影响', '函数零点的值或范围问题']正确率19.999999999999996%已知函数$$f ( x )=\operatorname{l o g}_{a} x-4^{x-1} ( a > 0$$且$${{a}{≠}{1}{)}}$$在$$\left( 0, \ \frac{1} {2} \right]$$上无零点,在$$\left( \frac{1} {2}, \, 1 \right)$$上有零点,则实数$${{a}}$$的取值范围为()
D
A.$$\left( 0, \ \frac{1} {4} \right)$$
B.$$\left( \frac{1} {4}, ~ 1 \right) \cup( 1, ~+\infty)$$
C.$$\left( 0, \enspace\frac{1} {4} \right]$$
D.$$\left( \frac{1} {4}, \, 1 \right)$$
3、['底数对对数函数图象的影响']正确率60.0%已知三个对数函数$$y=\operatorname{l o g}_{a} x, \, \, \, y=\operatorname{l o g}_{b} x, \, \, \, y=\operatorname{l o g}_{c} x ( a > 0, \, \, \, b > 0, \, \, \, c > 0,$$且$$a \neq1, \, \, \, b \neq1, \, \, \, c \neq1 ),$$它们分别对应图中序号为①②③的三个图像,则$$a, ~ b, ~ c$$的大小关系是()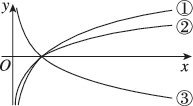
C
A.$$a < b < c$$
B.$$b < a < c$$
C.$$c < a < b$$
D.$$c < b < a$$
4、['底数对对数函数图象的影响', '底数对指数函数图象的影响']正确率40.0%已知$$a=x^{\frac{1} {3}}, b=\left( \frac{1} {3} \right)^{x}, c=\operatorname{l o g}_{\frac{1} {3}} x.$$则下列说法正确的是()
C
A.当$${{a}{=}{b}}$$时$${,{c}{<}{a}}$$
B.当$${{b}{=}{c}}$$时$${,{a}{<}{c}}$$
C.当$${{a}{=}{c}}$$时$${,{b}{<}{a}}$$
D.当$${{c}{=}{0}}$$时$${,{a}{<}{b}}$$
5、['底数对对数函数图象的影响', '底数对指数函数图象的影响']正确率60.0%已知$${{a}{>}{1}{,}}$$函数$${{y}{=}{{a}^{x}}}$$与$$y=\operatorname{l o g}_{a} (-x )$$的图像只可能是()
B
A.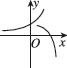
B.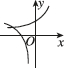
C.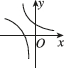
D.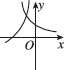
正确率40.0%已知函数$$f ( x )=\left( \frac{1} {2} \right)^{x}-x,$$$$g ( x )=$$$$\operatorname{l o g}_{\frac{1} {4}} x-x$$,$$h ( x )=x^{3}-x ( x > 0 )$$的零点分别为$$a, ~ b, ~ c,$$则$$a, ~ b, ~ c$$的大小关系为()
B
A.$$a > b > c$$
B.$$c > a > b$$
C.$$b > c > a$$
D.$$b > a > c$$
7、['底数对对数函数图象的影响', '充分、必要条件的判定', '对数(型)函数的单调性']正确率40.0%设$${{a}{,}{b}}$$均为不等于$${{1}}$$的正实数,则$$\4 a > b > 1^{n}$$是$$\mathrm{` `} \operatorname{l o g}_{b} 2 > \operatorname{l o g}_{a} 2^{n}$$的()
A
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
8、['底数对对数函数图象的影响', '函数性质的综合应用']正确率60.0%函数$$y=x \operatorname{s i n} x+l n \ ( \ x^{2}+1 )$$在$$[-\pi, \, \, \pi]$$上的图象大致为()
A
A.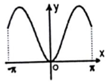
B.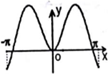
C.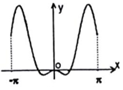
D.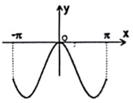
正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=\operatorname{l o g}_{3} x$$的图象与函数$${{g}{(}{x}{)}}$$的图象关于直线$${{y}{=}{x}}$$对称,函数$${{h}{(}{x}{)}}$$是最小正周期为$${{2}}$$的偶函数,且当$$x \in[ 0, ~ 1 ]$$时,$$h ~ ( \textbf{x} ) ~=g ~ ( \textbf{x} ) ~-1$$,若函数$$y=k \cdot f \textit{( x )}+h \textit{( x )}$$有$${{3}}$$个零点,则实数$${{k}}$$的取值范围是()
B
A.$$( 1, \ 2 \mathrm{l o g}_{7} 3 )$$
B.$$( \mathit{l}-\2, \mathit{l}-2 \operatorname{l o g}_{5} {3} )$$
C.$$( \mathbf{\theta}-2 \operatorname{l o g}_{5} 3, \mathbf{\phi}-1 )$$
D.$$( ~-\operatorname{l o g}_{7} 3, ~-\frac1 2 )$$
10、['底数对对数函数图象的影响', '反函数的性质', '函数零点存在定理']正确率60.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=a^{x}-l o g_{a} x \left( \begin{matrix} {a > 1} \\ \end{matrix} \right)$$有两个零点,则实数$${{a}}$$的取值范围是()
A
A.$$( {\bf1}, ~ e^{\frac{1} {e}} )$$
B.$$[ 2, ~ e^{e} )$$
C.$$( e^{\frac{1} {e}}, ~ e^{e} )$$
D.$$( \ e^{\frac{1} {e}}, \ e^{\frac{2} {e}} )$$
以下是各题的详细解析:
1. 解析:
题目条件为$$3^a > 3^b > 2$$,取对数得$$a > b > \log_3 2$$。分析$$\log_b 2 > \log_a 2$$:
由于$$a > b > \log_3 2$$,且$$\log_3 2 < 1$$,所以$$a > b > 1$$或$$1 > a > b > \log_3 2$$。
若$$a > b > 1$$,则$$\log_b 2 > \log_a 2$$成立;若$$1 > a > b$$,则$$\log_b 2 < \log_a 2$$。因此条件是充分不必要条件,选A。
2. 解析:
函数$$f(x) = \log_a x - 4^{x-1}$$在$$\left(0, \frac{1}{2}\right]$$无零点,在$$\left(\frac{1}{2}, 1\right)$$有零点。
由$$f\left(\frac{1}{2}\right) = \log_a \frac{1}{2} - 4^{-\frac{1}{2}} \leq 0$$,解得$$a \geq \frac{1}{4}$$。
在$$\left(\frac{1}{2}, 1\right)$$有零点,需$$f(1^-) = \log_a 1 - 4^{0^-} = 0^- - 1^- < 0$$,结合单调性分析得$$a \in \left(\frac{1}{4}, 1\right)$$,选D。
3. 解析:
观察图像:①上升最快,对应底数最大;②上升较慢,对应底数中等;③下降,对应底数小于1。
设①为$$y = \log_c x$$,②为$$y = \log_a x$$,③为$$y = \log_b x$$,则$$c > a > 1 > b$$,即$$b < a < c$$,选B。
4. 解析:
选项分析:
A. 当$$a = b$$时,$$x^{\frac{1}{3}} = \left(\frac{1}{3}\right)^x$$,解得$$x = \frac{1}{3}$$,此时$$c = \log_{\frac{1}{3}} \frac{1}{3} = 1$$,而$$a = \left(\frac{1}{3}\right)^{\frac{1}{3}} < 1$$,故$$c > a$$,A错误。
B. 当$$b = c$$时,$$\left(\frac{1}{3}\right)^x = \log_{\frac{1}{3}} x$$,解得$$x = \frac{1}{3}$$,此时$$a = \left(\frac{1}{3}\right)^{\frac{1}{3}} > \frac{1}{3} = c$$,B错误。
C. 当$$a = c$$时,$$x^{\frac{1}{3}} = \log_{\frac{1}{3}} x$$,解得$$x = \frac{1}{3}$$,此时$$b = \left(\frac{1}{3}\right)^{\frac{1}{3}} < \left(\frac{1}{3}\right)^{\frac{1}{3}} = a$$,C正确。
D. 当$$c = 0$$时,$$x = 1$$,此时$$a = 1$$,$$b = \frac{1}{3}$$,$$a > b$$,D错误。
综上,选C。
5. 解析:
$$a > 1$$时,$$y = a^x$$单调递增,$$y = \log_a (-x)$$定义域为$$x < 0$$且单调递增。只有选项D符合,选D。
6. 解析:
求零点:
$$f(x) = \left(\frac{1}{2}\right)^x - x = 0$$,解得$$a \approx 0.64$$。
$$g(x) = \log_{\frac{1}{4}} x - x = 0$$,解得$$b \approx 0.5$$。
$$h(x) = x^3 - x = 0$$,解得$$c = 1$$。
故$$c > a > b$$,选B。
7. 解析:
条件$$a > b > 1$$与$$\log_b 2 > \log_a 2$$等价,因为底数大于1时,对数函数单调递增,且$$\log_b 2 > \log_a 2 \Leftrightarrow \frac{1}{\log_2 b} > \frac{1}{\log_2 a} \Leftrightarrow \log_2 a > \log_2 b \Leftrightarrow a > b$$。
因此是充要条件,选C。
8. 解析:
函数$$y = x \sin x + \ln(x^2 + 1)$$为偶函数,排除B、D。当$$x \in (0, \pi)$$时,$$\sin x > 0$$,且$$\ln(x^2 + 1) > 0$$,故$$y > 0$$,排除C。选A。
9. 解析:
$$g(x) = 3^x$$(反函数),$$h(x)$$为偶函数且周期为2,当$$x \in [0,1]$$时,$$h(x) = 3^x - 1$$。
函数$$y = k \log_3 x + h(x)$$有3个零点,需$$k < 0$$且$$h(1) = 2$$,$$h(0) = 0$$,通过图像分析得$$k \in (-2 \log_5 3, -1)$$,选C。
10. 解析:
函数$$f(x) = a^x - \log_a x$$($$a > 1$$)有两个零点,需最小值小于0且$$f(1) = a > 0$$。
求导得极值点$$x_0 = \frac{\ln \ln a}{\ln a}$$,代入得$$a^{x_0} - \log_a x_0 < 0$$,解得$$a \in \left(e^{\frac{1}{e}}, e^e\right)$$,选C。
.jpg)