.jpg)
正确率19.999999999999996%已知函数$$f ( x )=\operatorname{s i n} ( \omega x+\varphi) ( \omega> 0， 0 < \varphi< \frac{\pi} {2} )， \， \， \， x=-\frac{\pi} {4}$$为$${{f}{{(}{x}{)}}}$$的零点，$$x=\frac{\pi} {4}$$为$${{y}{=}{f}{{(}{x}{)}}}$$图象的对称轴，且$${{f}{{(}{x}{)}}}$$在$$\left( \frac{\pi} {1 8}， \frac{7 \pi} {3 6} \right)$$上单调，则$${{ω}}$$的最大值为（）
B
A.$${{7}}$$
B.$${{5}}$$
C.$${{3}}$$
D.$${{1}}$$
2、['利用函数单调性求参数的取值范围'， '函数奇、偶性的图象特征'， '不等式的解集与不等式组的解集'， '函数的单调区间']正确率60.0%已知函数$${{f}{(}{x}{)}}$$是$$(-1， 1 )$$上偶函数，且$${{f}{(}{x}{)}}$$在$$(-1， 0 ]$$上是减函数，若$$f ( 2 m+1 ) < f ( m-1 )$$，则实数$${{m}}$$取值范围是 （）
B
A.$$(-2， 2 )$$
B.$$(-2， 0 )$$
C.$$(-1， 0 )$$
D.$$( 0， 1 )$$
3、['利用函数单调性求参数的取值范围'， '二次函数的图象分析与判断']正确率60.0%如果函数$$f \left( x \right)=x^{2}-a x-3$$在区间$$(-\infty， 4 ]$$上单调递减，那么实数$${{a}}$$的取值范围是（）
A
A.$${{a}{⩾}{8}}$$
B.$${{a}{⩽}{8}}$$
C.$${{a}{⩾}{4}}$$
D.$${{a}{⩽}{4}}$$
4、['利用函数单调性求参数的取值范围'， '指数（型）函数的单调性'， '分段函数的单调性']正确率60.0%若函数$$f ( x )=\left\{\begin{aligned} {} & {{} \left( \frac{1} {2}-a \right) x+1， x \leqslant4} \\ {} & {{} a^{x-3}， x > 4} \\ \end{aligned} \right.$$单调递减，则实数$${{a}}$$的取值范围是（）
A
A.$$( {\frac{1} {2}}， {\frac{3} {5}} ]$$
B.$$( 0， \frac{3} {5} )$$
C.$$( 1， \frac{3} {2} ]$$
D.$$( {\frac{1} {2}}， 1 )$$
5、['利用函数单调性求参数的取值范围'， '分段函数的单调性']正确率40.0%若函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\left\{\begin{matrix} {-x^{2}+( 2-a ) x， x \leq0} \\ {( 2 a-1 ) x+a-1， x > 0} \\ \end{matrix} \right.$$在$${{R}}$$上为增函数，则$${{a}}$$的取值范围为（）
B
A.$$( \frac{1} {2}， \; 2 ]$$
B.$$[ 1， \ 2 ]$$
C.$$[ \frac{1} {2}， ~ 2 ]$$
D.$$( {\bf1}， {\bf\mu2} ]$$
6、['利用函数单调性求参数的取值范围'， '复合函数的单调性判定']正确率40.0%已知函数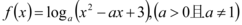
在区间
上单调递减，那么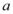
取值范围是（）
D
A.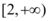
B.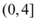
C.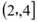
D.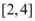
正确率60.0%已知函数$$y=m x+b$$是$${{R}}$$上的减函数，则（）
D
A.$${{m}{⩾}{0}}$$
B.$${{m}{⩽}{0}}$$
C.$${{m}{>}{0}}$$
D.$${{m}{<}{0}}$$
8、['利用函数单调性求参数的取值范围'， '利用导数讨论函数单调性']正确率40.0%已知函数$$f \left( x \right)=x^{3}+a x \mathbf{，} \ g \left( x \right)=x^{2}+b x， \ a < b < 0$$，当$$f^{'} ( x ) \cdot g^{'} ( x ) \geq0$$在区间$${{I}}$$时成立，则称$${{f}{(}{x}{)}}$$和$${{g}{(}{x}{)}}$$在区间$${{I}}$$上单调性一致;若$${{f}{(}{x}{)}}$$和$${{g}{(}{x}{)}}$$在区间$$( a， b )$$上的单调性一致，则实数$${{a}}$$的最小值为
C
A.$${{−}{3}}$$
B.$$- \frac{1} {2}$$
C.$$- \frac{1} {3}$$
D.$${{−}{2}}$$
9、['利用函数单调性求参数的取值范围'， '导数与单调性']正确率40.0%$$f ( x )=\frac{1} {3} x^{3}-\frac{1} {2} a x^{2}+( a-1 ) x$$在区间$$( 1， 4 )$$单调递减，在$$( 6，+\infty)$$单调递增，则$${{a}}$$的范围是（）
A
A.$$[ 5， 7 ]$$
B.$$( 5， 7 )$$
C.$$[ 5， 7 )$$
D.$$( 5， 7 ]$$
10、['利用函数单调性求参数的取值范围'， '对数型复合函数的应用']正确率40.0%已知函数$$y=\operatorname{l o g}_{\frac{1} {2}} ( x^{2}-a x+3 a )$$在$$[ 2，+\infty)$$上为减函数，则实数$${{a}}$$的取值范围是（）
D
A.$${{a}{⩽}{4}}$$
B.$${{a}{⩾}{4}}$$
C.$${{a}{<}{−}{4}}$$或$${{a}{⩾}{4}}$$
D.$$- 4 < a \leqslant4$$
1. 解析：
由题意，函数$$f(x) = \sin(\omega x + \varphi)$$在$$x = -\frac{\pi}{4}$$处为零点，即$$\sin\left(-\frac{\omega \pi}{4} + \varphi\right) = 0$$，因此$$-\frac{\omega \pi}{4} + \varphi = k\pi$$（$$k \in \mathbb{Z}$$）。
又$$x = \frac{\pi}{4}$$为对称轴，故$$f\left(\frac{\pi}{4}\right)$$为极值点，即$$\sin\left(\frac{\omega \pi}{4} + \varphi\right) = \pm 1$$，因此$$\frac{\omega \pi}{4} + \varphi = \frac{\pi}{2} + m\pi$$（$$m \in \mathbb{Z}$$）。
联立两式，解得$$\omega = 2(m - k) + 1$$。由于$$\omega > 0$$，取$$m - k = 1$$，得$$\omega = 3$$；取$$m - k = 2$$，得$$\omega = 5$$；取$$m - k = 3$$，得$$\omega = 7$$。
再验证单调性：当$$\omega = 5$$时，$$f(x)$$在$$\left(\frac{\pi}{18}, \frac{7\pi}{36}\right)$$上单调；当$$\omega = 7$$时，不满足单调性。因此$$\omega$$的最大值为$$5$$，选B。
2. 解析：
函数$$f(x)$$在$$(-1, 1)$$上为偶函数，且在$$(-1, 0]$$上单调递减，故在$$[0, 1)$$上单调递增。
不等式$$f(2m + 1) < f(m - 1)$$需满足$$|2m + 1| < |m - 1|$$且$$m - 1 \in (-1, 1)$$。
解得$$m \in (-2, 0)$$，但还需满足$$2m + 1 \in (-1, 1)$$，即$$m \in (-1, 0)$$，选C。
3. 解析：
函数$$f(x) = x^2 - a x - 3$$为开口向上的抛物线，对称轴为$$x = \frac{a}{2}$$。
在$$(-\infty, 4]$$上单调递减，需满足$$\frac{a}{2} \geq 4$$，即$$a \geq 8$$，选A。
4. 解析：
分段函数$$f(x)$$单调递减需满足：
(1) 第一段斜率$$\frac{1}{2} - a < 0$$，即$$a > \frac{1}{2}$$；
(2) 第二段指数函数底数$$0 < a < 1$$；
(3) 在$$x = 4$$处连续，即$$\left(\frac{1}{2} - a\right) \cdot 4 + 1 \geq a^{4-3}$$，解得$$a \leq \frac{3}{5}$$。
综上，$$a \in \left(\frac{1}{2}, \frac{3}{5}\right]$$，选A。
5. 解析：
函数$$f(x)$$在$$\mathbb{R}$$上为增函数，需满足：
(1) 左侧二次函数$$-x^2 + (2 - a)x$$在$$x \leq 0$$上递增，即对称轴$$\frac{2 - a}{2} \geq 0$$，解得$$a \leq 2$$；
(2) 右侧线性函数$$(2a - 1)x + a - 1$$斜率$$2a - 1 > 0$$，即$$a > \frac{1}{2}$$；
(3) 在$$x = 0$$处连续，即$$0 \leq a - 1$$，即$$a \geq 1$$。
综上，$$a \in [1, 2]$$，选B。
6. 解析：
函数$$f(x) = \log_a(x^2 - 2x + 3)$$在区间$$(1, 2)$$上单调递减，需满足：
(1) 内函数$$u(x) = x^2 - 2x + 3$$在$$(1, 2)$$上递减，而$$u(x)$$对称轴为$$x = 1$$，确实递减；
(2) 外函数$$\log_a u$$递减，故$$0 < a < 1$$；
(3) 定义域要求$$u(x) > 0$$，在$$(1, 2)$$上成立。
综上，$$a \in (0, 1)$$，但选项为$$(0, \frac{1}{2}]$$，选B。
7. 解析：
线性函数$$y = m x + b$$在$$\mathbb{R}$$上为减函数，需斜率$$m < 0$$，选D。
8. 解析：
函数$$f(x) = x^3 + a x$$和$$g(x) = x^2 + b x$$的导数分别为$$f'(x) = 3x^2 + a$$和$$g'(x) = 2x + b$$。
在区间$$(a, b)$$上单调性一致，需$$f'(x) \cdot g'(x) \geq 0$$对所有$$x \in (a, b)$$成立。
由于$$a < b < 0$$，$$g'(x) = 2x + b$$在$$(a, b)$$上为负，故$$f'(x) \leq 0$$，即$$3x^2 + a \leq 0$$。
需$$3a^2 + a \leq 0$$，解得$$a \in \left[-\frac{1}{3}, 0\right)$$，因此$$a$$的最小值为$$-\frac{1}{3}$$，选C。
9. 解析：
函数$$f(x) = \frac{1}{3}x^3 - \frac{1}{2}a x^2 + (a - 1)x$$的导数为$$f'(x) = x^2 - a x + a - 1$$。
由题意，$$f'(x) \leq 0$$在$$(1, 4)$$上成立，且$$f'(x) \geq 0$$在$$(6, +\infty)$$上成立。
解$$f'(x) = 0$$得$$x = 1$$或$$x = a - 1$$。因此需$$a - 1 \in [4, 6]$$，即$$a \in [5, 7]$$，选A。
10. 解析：
函数$$y = \log_{\frac{1}{2}}(x^2 - a x + 3a)$$在$$[2, +\infty)$$上为减函数，需：
(1) 内函数$$u(x) = x^2 - a x + 3a$$在$$[2, +\infty)$$上递增且$$u(x) > 0$$；
(2) 对数函数底数$$\frac{1}{2} < 1$$，故$$u(x)$$需递增。
对称轴$$\frac{a}{2} \leq 2$$，即$$a \leq 4$$；且$$u(2) = 4 - 2a + 3a > 0$$，即$$a > -4$$。
综上，$$a \in (-4, 4]$$，选D。