正确率60.0%若$$y=f ~ ( x )$$是定义域在$${{R}}$$上的函数,则$$y=f ~ ( x )$$为奇函数的一个充要条件为()
D
A.$$f \left( \begin{matrix} {0} \\ \end{matrix} \right) \ =0$$
B.对$$\forall x \in R, ~ f ~ ( \textbf{x} ) ~=0$$都成立
C.$$\exists x_{0} \in R,$$使得$$f ~ ( \boldsymbol{x}_{0} ) ~+f ~ ( \boldsymbol{\omega}-\boldsymbol{x}_{0} ) ~=0$$
D.对$$\forall x \in R, ~ f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~+f \left( \begin{matrix} {\rho} \\ {-x} \\ \end{matrix} \right) ~=0$$都成立
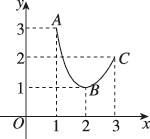
2、['函数求值']正确率80.0%已知函数$$y=g ( x )$$的对应关系如下表所示,函数$$y=f ( x )$$的图象如图所示,则$$g [ f ( 1 ) ]$$的值为()
| $${{x}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{g}{(}{x}{)}}$$ | $${{4}}$$ | $${{3}}$$ | $${{−}{1}}$$ |
A
A.$${{−}{1}}$$
B.$${{0}}$$
C.$${{3}}$$
D.$${{4}}$$
3、['函数求值', '列表法']正确率60.0%已知函数$${{f}{(}{x}{)}}$$和$${{g}{(}{x}{)}}$$分别由下表给出,则满足$$f ( g ( x ) ) > g ( f ( x ) )$$的$${{x}}$$的取值范围是()
| $${{x}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{f}{(}{x}{)}}$$ | $${{1}}$$ | $${{3}}$$ | $${{2}}$$ |
| $${{x}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ |
| $${{g}{(}{x}{)}}$$ | $${{2}}$$ | $${{1}}$$ | $${{3}}$$ |
C
A.$$\{1, 2, 3 \}$$
B.$$\{1, 2 \}$$
C.$$\{1, 3 \}$$
D.$${{\{}{1}{\}}}$$
4、['函数求值', '二次函数的图象分析与判断']正确率60.0%函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=a x^{2}+b x+8$$满足条件$$f \ ( \ -1 ) \ =f \ ( \ 3 )$$,则$${{f}{(}{2}{)}}$$的值为()
C
A.$${{5}}$$
B.$${{6}}$$
C.$${{8}}$$
D.与$${{a}{,}{b}}$$值有关
5、['由图象(表)求三角函数的解析式', '函数求值', '三角函数的图象变换']正确率40.0%将函数$$f ~ ( \textbf{x} ) ~=-\frac{1} {2} \operatorname{c o s} 2 x$$的图象向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位长度后,再将图象上各点的纵坐标伸长到原来的$${{2}}$$倍,得到函数$$y=g \emph{\left( x \right)}$$的图象,则$$g ~ ( \frac{3 \pi} {4} ) ~=~ ($$)
A
A.$$\frac{\sqrt3} {2}$$
B.$$- \frac{\sqrt3} {2}$$
C.$$- \frac{1} {2}$$
D.$$\frac{1} {2}$$
6、['函数奇偶性的应用', '函数的周期性', '函数求值']正确率19.999999999999996%对任意的实数$${{x}}$$,奇函数$${{f}{(}{x}{)}}$$满足$$f ( x )=-f ( x+2 )$$,且在$$[ 0, 2 ]$$上的解析式为$$f ( x )=\{\begin{array} {l l} {\quad x^{2}, 0 \leqslant x \leqslant1} \\ {\quad\operatorname{l o g}_{2} x+1, 1 < x \leqslant2} \\ \end{array}$$,则$$f ( 2 0 1 8 )+f ( 2 0 1 9 )=\c($$)
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
7、['函数奇偶性的应用', '函数的周期性', '函数求值']正确率60.0%已知$${{f}{(}{x}{)}}$$在$${{R}}$$上为奇函数,且满足$$f ( x+2 )=-f ( x )$$,则$${{f}{(}{6}{)}}$$的值为()
A
A.$${{0}}$$
B.$${{−}{1}}$$
C.$${{1}}$$
D.$${{2}}$$
8、['函数奇偶性的应用', '利用函数奇偶性求值', '函数求值', '函数的周期性']正确率40.0%已知$${{f}{(}{x}{)}}$$是定义在$${{R}}$$上的奇函数,且$${{f}{(}{x}{)}}$$的图象关于直线$${{x}{=}{2}}$$对称.若当$$0 < x \leqslant2$$时,$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=x+1$$,则$$f ~ ( \mathrm{\bf{2 0 1 9}} ) ~+f ~ ( \mathrm{\bf{2 0 2 0}} ) ~=$$()
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{4}}$$
9、['函数求值']正确率60.0%若$$f ~ ( \textup{x}+2 ) ~=2 x+3$$,则$${{f}{(}{5}{)}}$$的值是()
A
A.$${{9}}$$
B.$${{7}}$$
C.$${{5}}$$
D.$${{3}}$$
10、['函数求值', '函数求解析式']正确率60.0%函数$${{f}{(}{x}{)}}$$满足,则$$f ~ ( \varrho-1 ) ~=~ ($$)
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{−}{1}}$$
D.$${{2}}$$
1. 奇函数的定义是 $$f(-x) = -f(x)$$ 对所有 $$x \in \mathbb{R}$$ 成立。选项 D 明确表达了这一条件,因此是充要条件。选项 A 和 B 是必要条件但不是充分条件,选项 C 仅针对特定 $$x_0$$ 成立,不满足全局性。
3. 分别计算 $$f(g(x))$$ 和 $$g(f(x))$$ 的值: - 当 $$x=1$$ 时,$$f(g(1))=f(2)=3$$,$$g(f(1))=g(1)=2$$,满足不等式。 - 当 $$x=2$$ 时,$$f(g(2))=f(1)=1$$,$$g(f(2))=g(3)=3$$,不满足。 - 当 $$x=3$$ 时,$$f(g(3))=f(3)=2$$,$$g(f(3))=g(2)=1$$,满足。 因此,满足条件的 $$x$$ 是 1 和 3,答案为 C。
5. 平移后的函数为 $$f\left(x-\frac{\pi}{6}\right)=-\frac{1}{2}\cos\left(2\left(x-\frac{\pi}{6}\right)\right)$$。纵坐标伸长 2 倍后为 $$g(x)=-cos\left(2x-\frac{\pi}{3}\right)$$。代入 $$x=\frac{3\pi}{4}$$ 得 $$g\left(\frac{3\pi}{4}\right)=-cos\left(\frac{3\pi}{2}-\frac{\pi}{3}\right)=-cos\left(\frac{7\pi}{6}\right)=\frac{\sqrt{3}}{2}$$,答案为 A。
7. 由 $$f(x+2)=-f(x)$$ 和奇函数性质 $$f(0)=0$$,推导得 $$f(6)=f(2+4)=-f(2)=f(0)=0$$,答案为 A。
9. 设 $$t=x+2$$,则 $$x=t-2$$,代入得 $$f(t)=2(t-2)+3=2t-1$$。因此 $$f(5)=2 \times 5 -1=9$$,答案为 A。
.jpg)