正确率80.0%函数$$f ( x )=\frac{1} {\sqrt{2-x}}+( x+2 )^{0}$$的定义域为()
B
A.$$(-\infty, ~ 2 ) \cup( 2, ~+\infty)$$
B.$$(-\infty, ~-2 ) \cup(-2, ~ 2 )$$
C.$$(-\infty, ~-2 )$$
D.$$(-\infty, \; 2 )$$
2、['利用导数讨论函数单调性', '函数单调性的判断', '函数求定义域']正确率60.0%下面关于函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=1-\frac{1} {x}$$的说法正确的是()
B
A.在定义域上为增函数
B.在$$( \mathrm{\mathbf{~-\infty, \ 0 ~}} )$$上是增函数
C.在定义域上为减函数
D.在$$( \mathrm{\mathbf{~-\infty, \ 0 ~}} )$$上为减函数
3、['函数求定义域']正确率60.0%函数$$y=\frac{( 2 x-1 )^{\frac{3} {4}}} {( 2-x )^{\frac{1} {2}}}$$的定义域为$${{(}{)}}$$
C
A.$$[ \frac{1} {2},+\infty)$$
B.$$[ \frac{1} {2}, 2 ) \cup( 2,+\infty)$$
C.$$[ \frac{1} {2}, 2 )$$
D.$$(-\infty, 2 )$$
4、['一元二次不等式的解法', '函数求定义域']正确率60.0%函数$$f ( x )=\sqrt{( x+1 ) ( x-2 )}+( x+2 )^{0}$$,则其定义域为$${{(}{)}}$$
C
A.$$\{x | x \leqslant-1$$或$${{x}{⩾}{2}}$$
B.$$\{x |-1 \leqslant x \leqslant2 \}$$
C.$$\{x | x \leqslant-1$$或$${{x}{⩾}{2}}$$,且$$x \neq-2 \}$$
D.$$\{x | x <-2$$或$${{x}{⩾}{1}{\}}}$$
5、['不等式的解集与不等式组的解集', '函数求定义域']正确率60.0%函数$$f ( x )=\frac{\sqrt{x+2}} {x-3}+\left( x+2 \right)^{0}$$的定义域为()
D
A.$$[-2 \,, \,+\infty)$$
B.$$(-2 \,, \,+\infty)$$
C.$$[-2, \, 3 ) \bigcup( 3 \,, \,+\infty)$$
D.$$(-2 \,, \, 3 ) \bigcup( 3 \,, \,+\infty)$$
6、['函数求值域', '图象法', '函数求定义域']正确率60.0%已知函数$${{f}{(}{x}{)}}$$的图象如图所示,则该函数的定义域$${、}$$值域分别是$${{(}{)}}$$。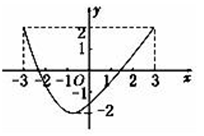
D
A.$$(-3, 3 ) \,, (-2, 2 )$$
B.$$(-2, 2 ) \, \,, (-3, 3 )$$
C.$$[-2, 2 ] \,, [-3, 3 ]$$
D.$$[-3, 3 ] \;, [-2, 2 ]$$
7、['对数(型)函数的定义域', '对数方程与对数不等式的解法', '函数求定义域']正确率40.0%函数$${{f}{{(}{x}{)}}{=}{\sqrt {{1}{−}{{l}{n}}{x}}}}$$的定义域是()
B
A.$$(-\infty, e ]$$
B.$$( 0, e ]$$
C.$$[ e,+\infty)$$
D.$$( 0, e )$$
8、['对数(型)函数的定义域', '函数求定义域']正确率60.0%函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=\frac{\sqrt{x+3}+l n ( 1-x )} {x+3}$$的定义域为()
C
A.$$[-3, \ 1 )$$
B.$$[-3, ~ 1 ]$$
C.$$( \ -3, \ 1 )$$
D.$$( \ -3, \ 1 ]$$
9、['函数求定义域']正确率60.0%函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=\frac{1} {x-5}+\sqrt{x-1}$$的定义域为()
C
A.$$( \mathrm{~-\infty, \ 1 ~} )$$
B.$$[ 1, ~+\infty)$$
C.$$[ 1, \ 5 ) \cup\begin{array} {c c} {( 5, \ l+\infty)} \\ \end{array}$$
D.
正确率60.0%函数$$f ( x )=\sqrt{3-3^{-x}}+\operatorname{l n} | x |$$的定义域为()
B
A.$$[-1,+\infty)$$
B.$$[-1, 0 ) \cup( 0,+\infty)$$
C.$$(-\infty,-1 ]$$
D.$$(-1, 0 ) \cup( 0,+\infty)$$
1. 解析:函数$$f(x)=\frac{1}{\sqrt{2-x}}+(x+2)^0$$的定义域需满足两个条件:
(1) 分母$$\sqrt{2-x}$$要求$$2-x>0$$,即$$x<2$$;
(2) 零次幂$$(x+2)^0$$要求$$x+2\neq0$$,即$$x\neq-2$$。
综上,定义域为$$(-\infty,-2)\cup(-2,2)$$,故选 B。
2. 解析:函数$$f(x)=1-\frac{1}{x}$$的定义域为$$x\neq0$$。
求导得$$f'(x)=\frac{1}{x^2}>0$$($$x\neq0$$),故函数在$$(-\infty,0)$$和$$(0,+\infty)$$上均为增函数,但整体定义域上不连续,不能直接说在定义域上为增函数。因此选项 B 正确。
3. 解析:函数$$y=\frac{(2x-1)^{\frac{3}{4}}}{(2-x)^{\frac{1}{2}}}$$需满足:
(1) 根号内$$2x-1\geq0$$,即$$x\geq\frac{1}{2}$$;
(2) 分母$$(2-x)^{\frac{1}{2}}$$要求$$2-x>0$$,即$$x<2$$。
综上,定义域为$$[\frac{1}{2},2)$$,故选 C。
4. 解析:函数$$f(x)=\sqrt{(x+1)(x-2)}+(x+2)^0$$需满足:
(1) 根号内$$(x+1)(x-2)\geq0$$,解得$$x\leq-1$$或$$x\geq2$$;
(2) 零次幂$$(x+2)^0$$要求$$x+2\neq0$$,即$$x\neq-2$$。
综上,定义域为$$x\leq-1$$或$$x\geq2$$且$$x\neq-2$$,故选 C。
5. 解析:函数$$f(x)=\frac{\sqrt{x+2}}{x-3}+(x+2)^0$$需满足:
(1) 根号内$$x+2\geq0$$,即$$x\geq-2$$;
(2) 分母$$x-3\neq0$$,即$$x\neq3$$;
(3) 零次幂$$(x+2)^0$$要求$$x+2\neq0$$,即$$x\neq-2$$。
综上,定义域为$$[-2,3)\cup(3,+\infty)$$,但题目选项未严格排除$$x=-2$$,最接近的是 C。
6. 解析:根据图像,函数$$f(x)$$的横坐标范围为$$[-3,3]$$(定义域),纵坐标范围为$$[-2,2]$$(值域),故选 D。
7. 解析:函数$$f(x)=\sqrt{1-\ln x}$$需满足$$1-\ln x\geq0$$且$$x>0$$,即$$0 8. 解析:函数$$f(x)=\frac{\sqrt{x+3}+\ln(1-x)}{x+3}$$需满足: 9. 解析:函数$$f(x)=\frac{1}{x-5}+\sqrt{x-1}$$需满足: 10. 解析:函数$$f(x)=\sqrt{3-3^{-x}}+\ln|x|$$需满足:
(1) 根号内$$x+3\geq0$$,即$$x\geq-3$$;
(2) 对数$$\ln(1-x)$$要求$$1-x>0$$,即$$x<1$$;
(3) 分母$$x+3\neq0$$,即$$x\neq-3$$。
综上,定义域为$$[-3,1)$$,故选 A。
(1) 分母$$x-5\neq0$$,即$$x\neq5$$;
(2) 根号内$$x-1\geq0$$,即$$x\geq1$$。
综上,定义域为$$[1,5)\cup(5,+\infty)$$,故选 C。
(1) 根号内$$3-3^{-x}\geq0$$,即$$3^{-x}\leq3$$,解得$$x\geq-1$$;
(2) 对数$$\ln|x|$$要求$$|x|>0$$,即$$x\neq0$$。
综上,定义域为$$[-1,0)\cup(0,+\infty)$$,故选 B。
.jpg)