.jpg)
正确率60.0%已知函数$${{f}{(}{x}{)}}$$在定义域$$( 0， ~+\infty)$$上是单调函数，若对任意$$x \in( 0， ~ ~+\infty)，$$都有$$f \left[ f ( x )-\frac{1} {x} \right]=2，$$则$$f \left( \frac1 {2 0 2 4} \right)=$$（）
D
A.$$\frac{1} {2 0 2 4}$$
B.$${{2}{0}{2}{3}}$$
C.$${{2}{0}{2}{4}}$$
D.$${{2}{0}{2}{5}}$$
2、['函数求值'， '函数求解析式'， '利用基本不等式求最值']正确率40.0%已知$$f \left( x+\frac{1} {x} \right)=x^{2}+\frac{1} {x^{2}}，$$则$${{f}{(}{3}{)}}$$的值为（）
C
A.$${{3}}$$
B.$${{5}}$$
C.$${{7}}$$
D.$$\frac{7} {2}$$
3、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '三角函数的图象变换'， '函数求解析式']正确率40.0%将函数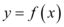
图象上每一点的纵坐标保持不变，横坐标扩大到原来的
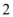倍，再把所得的图象沿
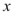轴向右平移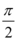
个单位，这样所得的曲线与
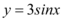的图象相同，则函数
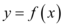的表达式是$${{(}{)}}$$
B
A.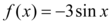
B.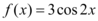
C.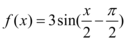
D.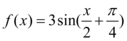
正确率40.0%函数$$f ( x )=x | x-a |$$，若$$\forall x_{1}， x_{2} \in[ 3，+\infty)， x_{1} \neq x_{2}，$$不等式$$\frac{f ( x_{1} )-f ( x_{2} )} {x_{1}-x_{2}} > 0$$恒成立，则实数$${{a}}$$的取值范围是$${{(}{)}}$$
C
A.$$(-\infty，-3 ]$$
B.$$[-3， 0 )$$
C.$$(-\infty， 3 ]$$
D.$$( 0， 3 ]$$
5、['函数求解析式'， '函数单调性的应用']正确率60.0%已知函数$${{f}{（}{x}{）}}$$在定义域$$( \mathrm{\bf~ 0}， \mathrm{\bf~ \Lambda}+\infty)$$上是单调函数，若对于任意$$x \in~ ( 0， ~+\infty) ~， ~ f ( f ( x )-\frac{1} {x} )=2$$，则函数$${{f}{（}{x}{）}}$$的解析式是（）
D
A.$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right) \ =x$$
B.$$f ( x )=\frac{1} {x}$$
C.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=x+1$$
D.$$f ( x )=\frac{1} {x}+1$$
6、['函数奇偶性的应用'， '函数求解析式'， '利用函数奇偶性求解析式']正确率60.0%已知定义在$${{R}}$$上的奇函数$${{f}{（}{x}{）}}$$，当$${{x}{>}{0}}$$时，$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=x^{2}+| x |-1$$，那么$${{x}{<}{0}}$$时，$${{f}{（}{x}{）}}$$的解析式为$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\cline{(}$$）
D
A.$$x^{2}-| x |+1$$
B.$$- x^{2}+| x |+1$$
C.$$- x^{2}-| x |-1$$
D.$$- x^{2}-| x |+1$$
7、['函数奇偶性的应用'， '函数求解析式']正确率60.0%设$${{f}{{(}{x}{)}}}$$是定义在$${{R}}$$上的周期为$${{2}}$$的偶函数，已知$$x \in[ 2， ~ 3 ]$$时，$${{f}{{(}{x}{)}}{=}{x}}$$，则$$x \in[-2， ~ 0 ]$$时，$${{f}{{(}{x}{)}}}$$的解析式为$${{f}{{(}{x}{)}}{=}}$$（）
C
A.$${{x}{+}{4}}$$
B.$${{2}{−}{x}}$$
C.$$3-| x+1 |$$
D.$$2+| x+1 |$$
8、['函数单调性的判断'， '函数求解析式'， '函数零点存在定理']正确率40.0%已知函数$${{f}{(}{x}{)}}$$是定义在$$( 0，+\infty)$$上的单调函数，$$\forall x \in( 0，+\infty)， f \left[ f ( x )-\operatorname{l n} x \right]=e+1$$，则函数$$g ( x )=f ( x )-f^{\prime} ( x )-e ($$其中$${{e}}$$为自然对数的底数)的零点所在的区间是（）
D
A.$$( 2， 3 )$$
B.$$( 0， \frac{1} {2} )$$
C.$$( {\frac{1} {2}}， 1 )$$
D.$$( 1， 2 )$$
9、['函数奇偶性的应用'， '函数求解析式']正确率60.0%已知函数$${{y}{=}{f}{{(}{x}{)}}}$$是定义在$${{R}}$$上的奇函数，当$${{x}{⩾}{0}}$$时，$$f \left( x \right)=x \left( 1+3 x \right)$$，则当$${{x}{<}{0}}$$时，$${{f}{{(}{x}{)}}}$$表达式是
$${}$$
D
A.$$- x \， ( 1+3 x )$$
B.$$x \， ( 1+3 x )$$
C.$$- x \， ( 1-3 x )$$
D.$$x \， ( 1-3 x )$$
10、['函数图象的识别'， '函数求解析式']正确率60.0%函数$$y=f ~ ( x )$$的图象如图所示，则$${{f}{（}{x}{）}}$$的解析式可以是（）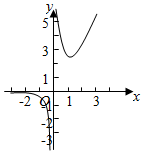
C
A.$$y=\frac{1} {x}+x^{2}$$
B.$$y=\frac{l n x} {x}$$
C.$$y=\frac{e^{x}} {x}$$
D.$$f \left( \textbf{x} \right) ~=x^{3}+l n | x |$$
1. 由于函数 $$f(x)$$ 在 $$(0, +\infty)$$ 上单调，且 $$f\left[f(x)-\frac{1}{x}\right]=2$$ 对所有 $$x>0$$ 成立，说明 $$f(x)-\frac{1}{x}$$ 是一个常数。设 $$f(x)-\frac{1}{x} = C$$，则 $$f(C)=2$$。代入 $$x=C$$ 得 $$f(C)-\frac{1}{C}=C$$，即 $$2-\frac{1}{C}=C$$，解得 $$C=1$$。因此 $$f(x)=1+\frac{1}{x}$$，故 $$f\left(\frac{1}{2024}\right)=1+2024=2025$$。答案为 D。
2. 设 $$t=x+\frac{1}{x}$$，则 $$x^2+\frac{1}{x^2}=t^2-2$$，所以 $$f(t)=t^2-2$$。因此 $$f(3)=3^2-2=7$$。答案为 C。
3. 设原函数为 $$y=\sin(2x)$$。横坐标扩大 2 倍得到 $$y=\sin(x)$$，再向右平移 $$\frac{\pi}{2}$$ 单位得到 $$y=\sin\left(x-\frac{\pi}{2}\right)=-\cos x$$。因此原函数为 $$y=\sin(2x)$$。答案为 D。
4. 函数 $$f(x)=x|x-a|$$ 在 $$[3,+\infty)$$ 上单调递增，需满足 $$a \leq 3$$。否则在 $$x=a$$ 处会出现极小值点，破坏单调性。答案为 C。
5. 同第 1 题，设 $$f(x)-\frac{1}{x}=C$$，由 $$f(C)=2$$ 解得 $$C=1$$，故 $$f(x)=1+\frac{1}{x}$$。答案为 D。
6. 设 $$x<0$$，则 $$-x>0$$，由奇函数性质得 $$f(x)=-f(-x)=-\left((-x)^2+|-x|-1\right)=-x^2-|x|+1$$。答案为 D。
7. 函数周期为 2 且为偶函数。当 $$x \in [-2,-1]$$ 时，$$x+4 \in [2,3]$$，故 $$f(x)=f(x+4)=x+4$$；当 $$x \in [-1,0]$$ 时，$$-x \in [0,1]$$，由偶函数性质得 $$f(x)=f(-x)=-x+2$$。综合为 $$f(x)=3-|x+1|$$。答案为 C。
8. 设 $$f(x)-\ln x = C$$，由 $$f(C)=e+1$$ 得 $$C+\ln C=e+1$$，解得 $$C=e$$。故 $$f(x)=e+\ln x$$，$$g(x)=e+\ln x-\frac{1}{x}-e=\ln x-\frac{1}{x}$$。计算 $$g(1)=-1<0$$，$$g(2)=\ln 2-\frac{1}{2}>0$$，零点在 $$(1,2)$$。答案为 D。
9. 设 $$x<0$$，则 $$-x>0$$，由奇函数性质得 $$f(x)=-f(-x)=-(-x)(1+3(-x))=x(1-3x)$$。答案为 D。
10. 观察图像，函数在 $$x=0$$ 附近趋向于 $$+\infty$$，且 $$x \to +\infty$$ 时增长较快。选项 A 中 $$\frac{1}{x}+x^2$$ 符合此特征；选项 B 和 C 在 $$x \to 0^+$$ 时趋向于 $$-\infty$$；选项 D 在 $$x=0$$ 无定义。答案为 A。