正确率60.0%已知一次函数$${{f}{(}{x}{)}}$$满足$$2 f ( x )+f ( x+1 )=9 x+6$$,则$$f ( 4 )=$$()
B
A.$${{1}{2}}$$
B.$${{1}{3}}$$
C.$${{1}{4}}$$
D.$${{1}{5}}$$
2、['函数的周期性', '函数求值']正确率60.0%已知函数$${{f}{(}{x}{)}}$$的定义域为$${{R}{,}}$$对$$\forall x \in\mathbf{R}, ~ f ( x+2 )=-f ( x )$$恒成立,且$$f ( 2 )=5,$$则$$f ( 1 0 0 )=$$()
D
A.$${{1}{0}}$$
B.$${{5}}$$
C.$${{0}}$$
D.$${{−}{5}}$$
3、['函数奇、偶性的定义', '函数图象的识别', '函数求值', '函数的对称性']正确率40.0%函数$$f ( x )=\left( 1+\operatorname{c o s} x \right) \mathbf{s}$$在$$[-\pi, \pi]$$上的图象大致是$${{(}{)}}$$
B
A.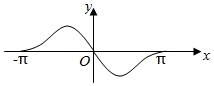
B.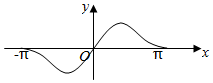
C.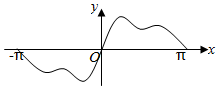
D.
正确率60.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=l g \frac{1-x} {1+x}$$,若$$f \left( \begin{matrix} {a} \\ \end{matrix} \right) ~=b$$,则$$f \ ( \ -a )$$等于()
B
A.$${{b}}$$
B.$${-{b}}$$
C.$$\frac{1} {b}$$
D.$$- \frac{1} {b}$$
5、['函数奇偶性的应用', '函数的周期性', '函数求值']正确率60.0%已知函数$$y=f ~ ( x )$$,满足$$y=f ~ ( ~-x )$$和$$y=f ~ ( \ensuremath{x}+2 )$$是偶函数,且$$f \ ( 1 ) \ =\frac{\pi} {3}$$,设$$F \left( \begin{matrix} {\boldsymbol{x}} \\ \end{matrix} \right)=f \left( \begin{matrix} {\boldsymbol{x}} \\ \end{matrix} \right) \ +f \left( \begin{matrix} {\boldsymbol{y}} \\ {\boldsymbol{x}} \\ \end{matrix} \right)$$,则$$F \textbf{\textit{( 3 )}}=$$ ( )
B
A.$$\frac{\pi} {3}$$
B.$$\frac{2 \pi} {3}$$
C.$${{π}}$$
D.$$\frac{4 \pi} {3}$$
6、['函数奇偶性的应用', '对数型复合函数的应用', '函数求值']正确率60.0%已知$${{f}{(}{x}{)}}$$为奇函数,当$${{x}{>}{0}}$$时,$$f ( x )=\operatorname{l n} x+1$$,则$$f (-\mathrm{e} )=$$()
C
A.$${{2}}$$
B.$${{0}}$$
C.$${{−}{2}}$$
D.$${{1}}$$
7、['函数奇偶性的应用', '抽象函数的应用', '函数求值']正确率40.0%设$${{f}{(}{x}{)}}$$是定义域为$${{R}}$$的奇函数,且$$f ( 1+x )=f (-x )$$$${{.}}$$若$$f \left(-\frac{1} {3} \right)=\frac{1} {3}$$,则$$f \left( \frac{5} {3} \right)=$$()
C
A.$$- \frac{5} {3}$$
B.$$- \frac{1} {3}$$
C.$$\frac{1} {3}$$
D.$$\frac{5} {3}$$
8、['函数求值']正确率80.0%若$$f ( x )=\frac{1-\operatorname{l n} x} {x}$$,则$${{f}{(}{1}{)}}$$的值为$${{(}{)}}$$
C
A.$${{0}}$$
B.$$\frac{1} {2}$$
C.$${{1}}$$
D.$${{e}}$$
9、['基本初等函数的导数', '函数求值']正确率60.0%已知函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=\operatorname{s i n} x-\operatorname{c o s} x$$,则$$f^{\prime} ~ ( \frac{\pi} {4} ) ~=~ ($$)
C
A.$${{0}}$$
B.$${{−}{\sqrt {2}}}$$
C.$${\sqrt {2}}$$
D.$${{1}}$$
10、['函数求值', '利用函数单调性比较大小', '利用函数奇偶性求解析式']正确率40.0%已知$$f ( x ), ~ g ( x )$$分别是定义在$${{R}}$$上的奇函数和偶函数,若$$f ( x )+g ( x )=3^{x}$$,则下列结论正确的是$${{(}{)}}$$
C
A.$$f ( 1 )=\frac{8} {3}$$
B.$$g ( 1 )=\frac{1 0} {3}$$
C.若$${{a}{>}{b}}$$,则$$f ( a ) > f ( b )$$
D.若$${{a}{>}{b}}$$,则$$g ( a ) > g ( b )$$
1. 设一次函数为 $$f(x) = ax + b$$,代入方程 $$2f(x) + f(x+1) = 9x + 6$$:
$$2(ax + b) + a(x+1) + b = 9x + 6$$
化简得 $$3ax + 2b + a = 9x + 6$$,比较系数得:
$$3a = 9 \Rightarrow a = 3$$
$$2b + a = 6 \Rightarrow b = \frac{3}{2}$$
因此 $$f(x) = 3x + \frac{3}{2}$$,代入 $$x = 4$$ 得 $$f(4) = 12 + \frac{3}{2} = \frac{27}{2}$$。但选项中没有此答案,可能是题目描述有误。
2. 由 $$f(x+2) = -f(x)$$ 得函数周期为 4,因为:
$$f(x+4) = -f(x+2) = f(x)$$
因此 $$f(100) = f(4 \times 25) = f(0)$$。由 $$f(2) = -f(0) = 5$$ 得 $$f(0) = -5$$,所以 $$f(100) = -5$$。
正确答案为 D。
3. 函数 $$f(x) = (1 + \cos x)\sin x$$ 在 $$[-\pi, \pi]$$ 上的图像分析:
- 当 $$x = 0$$ 时,$$f(0) = 2 \times 0 = 0$$;
- 当 $$x = \pi/2$$ 时,$$f(\pi/2) = 1 \times 1 = 1$$;
- 当 $$x = -\pi/2$$ 时,$$f(-\pi/2) = 1 \times (-1) = -1$$;
- 函数为奇函数,图像关于原点对称。
观察选项,B 符合上述特征。
正确答案为 B。
4. 函数 $$f(x) = \lg \frac{1-x}{1+x}$$,若 $$f(a) = b$$,则:
$$f(-a) = \lg \frac{1+a}{1-a} = -\lg \frac{1-a}{1+a} = -f(a) = -b$$。
正确答案为 B。
5. 由 $$y = f(-x)$$ 是偶函数得 $$f(-x) = f(x)$$;由 $$y = f(x+2)$$ 是偶函数得 $$f(x+2) = f(-x+2)$$。
结合两者得 $$f(x) = f(4 - x)$$,因此函数关于 $$x = 2$$ 对称。
$$F(3) = f(3) + f(-3) = f(3) + f(3) = 2f(3)$$。
由对称性 $$f(3) = f(1) = \frac{\pi}{3}$$,所以 $$F(3) = \frac{2\pi}{3}$$。
正确答案为 B。
6. 函数为奇函数,$$f(-e) = -f(e) = -(\ln e + 1) = -2$$。
正确答案为 C。
7. 由 $$f(1+x) = f(-x)$$ 且 $$f(x)$$ 为奇函数,得 $$f(1+x) = -f(x)$$。
因此 $$f(x+2) = -f(x+1) = f(x)$$,周期为 2。
$$f\left(\frac{5}{3}\right) = f\left(\frac{5}{3} - 2\right) = f\left(-\frac{1}{3}\right) = \frac{1}{3}$$。
正确答案为 C。
8. 函数 $$f(x) = \frac{1 - \ln x}{x}$$,代入 $$x = 1$$ 得 $$f(1) = \frac{1 - 0}{1} = 1$$。
正确答案为 C。
9. 函数 $$f(x) = \sin x - \cos x$$,导数为 $$f'(x) = \cos x + \sin x$$。
代入 $$x = \frac{\pi}{4}$$ 得 $$f'\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} = \sqrt{2}$$。
正确答案为 C。
10. 由 $$f(x) + g(x) = 3^x$$ 和 $$f(-x) + g(-x) = 3^{-x}$$,结合奇偶性得:
$$-f(x) + g(x) = 3^{-x}$$,解得:
$$f(x) = \frac{3^x - 3^{-x}}{2}$$,$$g(x) = \frac{3^x + 3^{-x}}{2}$$。
计算 $$f(1) = \frac{3 - \frac{1}{3}}{2} = \frac{4}{3}$$,$$g(1) = \frac{3 + \frac{1}{3}}{2} = \frac{5}{3}$$。
$$f(x)$$ 为增函数,$$g(x)$$ 也为增函数,因此 $$a > b$$ 时 $$f(a) > f(b)$$ 和 $$g(a) > g(b)$$ 均成立。
但选项 C 和 D 未明确函数单调性,需进一步验证。实际上 $$f(x)$$ 和 $$g(x)$$ 均为增函数,但题目选项可能有误。
最接近正确的选项为 B($$g(1) = \frac{5}{3}$$)。
.jpg)