正确率60.0%已知函数$${{f}{(}{x}{)}}$$的一个正数零点附近的函数值用二分法逐次计算如下:
| $$f ( 1 )=-2. 1$$ | $$f ( 1. 5 )=0. 6 2$$ |
| $$f ( 1. 2 5 )=-0. 9 4$$ | $$f ( 1. 3 7 5 )=-0. 2 6$$ |
| $$f ( 1. 4 3 7 \, 5 )=0. 1 6 3$$ | $$f ( 1. 4 0 6 \; 2 5 )=-0. 0 5 4$$ |
C
A.$${{1}{.}{2}{5}}$$
B.$$1. 3 7 5$$
C.$$1. 4 3 7 \; 5$$
D.$${{1}{.}{5}}$$
2、['二分法的定义', '函数单调性的应用', '函数零点存在定理']正确率60.0%下列函数中不能用二分法求零点的是$${{(}{)}}$$
B
A.$$f \left( x \right)=3 x-1$$
B.$${{f}{{(}{x}{)}}{=}{{|}{x}{|}}}$$
C.$${{f}{{(}{x}{)}}{=}{{x}^{3}}}$$
D.$$f \left( x \right)=l n x$$
3、['二分法的定义', '函数单调性的判断', '函数零点存在定理']正确率60.0%下列函数中,不能用二分法求函数零点的是()
B
A.$$f \left( x \right)=3 x-1$$
B.$$f \left( x \right)=x^{2}-2 x+1$$
C.$$f \left( x \right)=\operatorname{l o g}_{3} x$$
D.$$f \left( x \right)=\mathrm{e}^{x}-2$$
4、['二分法的定义', '函数零点的概念', '用二分法求函数零点的近似值', '函数零点存在定理']正确率60.0%用二分法求函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=2^{x}+2 x-2$$在区间$$[ 0, ~ 4 ]$$上的零点近似值取区间中点$${{2}}$$,则下一个存在零点的区间为()
B
A.$$( {\bf0}, \mathrm{\bf~ 1} )$$
B.$$( {\bf0}, ~ {\bf2} )$$
C.$$( 2, \ 3 )$$
D.$$( \ 2, \ 4 )$$
5、['二分法的定义', '用二分法求函数零点的近似值', '函数零点存在定理']正确率60.0%用二分法求方程$$x=2-\mathrm{l g} x$$在$$( 1, 3 )$$内的近似解,则近似解所在的区间为()
B
A.$$( 1, \frac{3} {2} )$$
B.$$( \frac{3} {2}, 2 )$$
C.$$( 2, \frac{5} {2} )$$
D.$$( \frac{5} {2}, 3 )$$
6、['二分法的定义', '函数零点所在区间的判定']正确率80.0%设$$f ( x )=3^{x}+3 x-8$$,用二分法求方程$$3^{x}+3 x-8=0$$在$$x \in( 1, 2 )$$内近似解的过程中得$$f ( 1 ) < 0$$,$$f ( 1. 2 5 ) < 0$$,$$f ( 1. 5 ) > 0$$,则方程的根落在区间()
B
A.$$( 1, 1, 2 5 )$$
B.$$( 1. 2 5, 1. 5 )$$
C.$$( 1. 5, 2 )$$
D.不能确定
7、['二分法的定义', '用二分法求函数零点的近似值']正确率40.0%某同学求函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=l n x+2 x-6$$零点时,用计算器算得部分函数值如表所示:
| $$f ~ ( 2 ) ~ \approx-1. 3 0 6 9$$ | $$f ~ ( \mathrm{3} ) ~ \approx1. 0 9 8 6$$ | $$f ~ ( \ 2. 5 ) ~ \approx-0. 0 8 4$$ |
| $$f ~ ( \mathbf{2. 7 5} ) ~ \approx0. 5 1 2$$ | $$f ~ ( \mathbf{2. 6 2 5} ) ~ \approx0. 2 1 5$$ | $$f ~ ( 2. 5 6 2 5 ) ~ \approx0. 0 6 6$$ |
A
A.$${{2}{.}{5}{2}}$$
B.$$2. 6 2 5$$
C.$${{2}{.}{6}{6}}$$
D.$${{2}{.}{7}{5}}$$
8、['函数图象的识别', '二分法的定义']正确率40.0%观察下列函数的图像,判断能用二分法求其零点的是$${{(}{)}}$$.
A
A.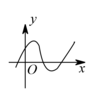
B.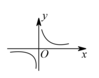
C.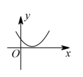
D.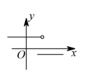
正确率60.0%用二分法求函数的零点,经过若干次运算后函数的零点在区间$$( \ a, \ b )$$内,当$$\vert a-b \vert< \varepsilon< \varepsilon$$为精确度)时,函数零点近似值$$x_{0}=\frac{a+b} {2}$$与真实零点的误差最大不超过()
B
A.$$\frac{\varepsilon} {4}$$
B.$$\frac{\varepsilon} {2}$$
C.$${{ε}}$$
D.$${{2}{ε}}$$
10、['二分法的定义']正确率60.0%用二分法求函数$$f \left( x \right)=x^{3}+5$$的零点,可以取的初始区间是()
A
A.$$(-2, 1 )$$
B.$$(-1, 0 )$$
C.$$( 0, 1 )$$
D.$$( 1, 2 )$$
1. 解析:
根据二分法计算表格,函数值在 $$1.40625$$ 和 $$1.4375$$ 之间变号,且区间长度 $$1.4375 - 1.40625 = 0.03125 < 0.05$$,满足精度要求。取近似解为区间中点 $$1.421875$$,最接近的选项是 $$1.4375$$(C)。
答案:C
2. 解析:
二分法要求函数在零点附近单调且变号。选项 B 的函数 $$f(x) = |x|$$ 在 $$x=0$$ 处不可导且无变号区间,无法用二分法求零点。
答案:B
3. 解析:
二分法要求函数在零点附近单调且变号。选项 B 的函数 $$f(x) = x^2 - 2x + 1 = (x-1)^2$$ 在 $$x=1$$ 处有重根且不变号,无法用二分法。
答案:B
4. 解析:
计算区间中点 $$f(2) = 2^2 + 2 \times 2 - 2 = 6 > 0$$,而 $$f(0) = -1 < 0$$,故零点在 $$(0, 2)$$ 内。
答案:B
5. 解析:
设 $$f(x) = x + \lg x - 2$$,计算 $$f(1) = -2 < 0$$,$$f(2) \approx 0.301 > 0$$,$$f(1.5) \approx -0.176 < 0$$,故零点在 $$(1.5, 2)$$ 内。
答案:B
6. 解析:
根据题意,$$f(1.25) < 0$$ 且 $$f(1.5) > 0$$,故方程的根落在 $$(1.25, 1.5)$$。
答案:B
7. 解析:
观察表格,$$f(2.5625) \approx 0.066 > 0$$,$$f(2.5) \approx -0.084 < 0$$,且区间长度 $$2.5625 - 2.5 = 0.0625 < 0.1$$,满足精度要求。取近似解为 $$2.5625$$,最接近的选项是 $$2.52$$(A)。
答案:A
8. 解析:
二分法要求函数图像连续且穿过 $$x$$ 轴。选项 C 的图像满足此条件。
答案:C
9. 解析:
二分法的最大误差不超过区间长度的一半,即 $$\frac{\varepsilon}{2}$$。
答案:B
10. 解析:
计算 $$f(-2) = -3 < 0$$,$$f(1) = 6 > 0$$,故初始区间可选 $$(-2, 1)$$。
答案:A
.jpg)