正确率80.0%用二分法求函数$${{f}{(}{x}{)}}$$在$$( a, \ b )$$内的唯一零点,精确度为$$0. 0 0 1,$$则结束计算的条件是()
B
A.$$| a-b | < \, 0. 1$$
B.$$| a-b | < \, 0. 0 0 1$$
C.$$| a-b | > 0. 0 0 1$$
D.$$| a-b |=0. 0 0 1$$
2、['用二分法求函数零点的近似值']正确率60.0%华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”“华氏不等式”“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”是研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每$${{1}{6}}$$人为一组,把每个人抽取的分泌物混合检查,若为阴性,则全部放行;若为阳性,则对这$${{1}{6}}$$人再次抽检确认感染者.某组$${{1}{6}}$$人中恰有一人感染(样本检验将会是阳性),若逐一检测可能需要$${{1}{5}}$$次才能确认感染者.现在先把这$${{1}{6}}$$人均分为$${{2}}$$组,选其中一组$${{8}}$$人的样本混合检查,若为阴性,则认定感染者在另一组;若为阳性,则认定感染者在本组.继续把认定的感染者所在的这组的$${{8}}$$人均分为$${{2}}$$组,选其中一组$${{4}}$$人的样本混合检查……以此类推,最终从这$${{1}{6}}$$人中确认那名感染者需要经过检测的次数为()
B
A.$${{3}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{7}}$$
4、['二分法的定义', '用二分法求函数零点的近似值']正确率40.0%求下列函数的零点,可以采用二分法的是()
B
A.$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right) ~=~ x^{4}$$
B.$$f ( \textbf{x} ) \ =\operatorname{t a n} x+2 \ ( \textbf{-} \frac{\pi} {2} < x < \frac{\pi} {2} )$$
C.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=\operatorname{c o s} x-1$$
D.$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=\left| 2^{x}-3 \right|$$
5、['函数零点所在区间的判定', '用二分法求函数零点的近似值', '函数单调性的应用']正确率40.0%用二分法求方程$$\operatorname{l g} x=3-x$$的近似解,可以取的一个区间是()
C
A.$$( 0, 1 )$$
B.$$( 1, 2 )$$
C.$$( 2, 3 )$$
D.$$( 3, 4 )$$
6、['用二分法求函数零点的近似值']正确率60.0%根据表格中的数据,可以断定方程$$\operatorname{l n} {x}+x-4=0$$的一个根所在的区间是()
| | $${{−}{{0}{.}{5}}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ |
| | $${{−}{{0}{.}{6}{9}}}$$ | $${{0}}$$ | $${{0}{.}{6}{9}}$$ | $${{1}{.}{1}{0}}$$ | $${{1}{.}{3}{9}}$$ |
C
A.$$(-0. 5, 1 )$$
B.$$( 1, 2 )$$
C.$$( 2, 3 )$$
D.$$( 3, 4 )$$
7、['用二分法求函数零点的近似值', '函数零点存在定理']正确率60.0%若函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=l o g_{3} x+x-3$$的一个零点附近的函数值用二分法逐次计算的参考数据如下:
| $$f ~ ( \ 2 ) ~=-0. 3 6 9 1$$ | $$f ~ ( \ 2. 5 ) ~=0. 3 3 4 0$$ |
| $$f ~ ( \ 2. 2 5 ) ~=-0. 0 1 1 9$$ | $$f ~ ( \ 2. 3 7 5 ) ~=0. 1 6 2 4$$ |
| $$f ~ ( \ 2. 3 1 2 5 ) ~=0. 0 7 5 6$$ | $$f ~ ( \ 2. 2 8 1 2 5 ) ~=0. 0 3 1 9$$ |
C
A.$${{2}{.}{1}}$$
B.$${{2}{.}{2}}$$
C.$${{2}{.}{2}{6}}$$
D.$${{2}{.}{4}}$$
8、['用二分法求函数零点的近似值']正确率60.0%下列函数中表示的函数能用二分法求零点的是()
C
A.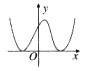
B.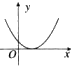
C.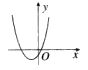
D.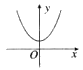
正确率60.0%已知函数$${{f}{(}{x}{)}}$$在$$( 1, 2 )$$内有$${{1}}$$个零点,用二分法求零点的近似值时,若精度为$${{0}{.}{0}{1}}$$,则至少计算中点函数值()
C
A.$${{5}}$$次
B.$${{6}}$$次
C.$${{7}}$$次
D.$${{8}}$$次
10、['函数零点的概念', '用二分法求函数零点的近似值']正确率60.0%下列是关于函数$$y=f ( x ), ~ x \in[ a, ~ b ]$$的说法:
①若$$x_{0} \in[ a, ~ b ],$$且满足$$f ( x_{0} )=0,$$则$$( x_{0}, 0 )$$是$${{f}{(}{x}{)}}$$的一个零点;
②若$${{x}_{0}}$$是$${{f}{(}{x}{)}}$$在$$[ a, ~ b ]$$上的零点,则可用二分法求$${{x}_{0}}$$的近似值;
③函数$${{f}{(}{x}{)}}$$的零点是方程$$f ( x )=0$$的根,但$$f ( x )=0$$的根不一定是函数$${{f}{(}{x}{)}}$$的零点;
④用二分法求方程的根时,得到的都是近似值.
则以上说法中正确的个数为()
A
A.$${{0}}$$
B.$${{1}}$$
C.$${{3}}$$
D.$${{4}}$$
1. 二分法结束的条件是区间长度小于精确度,即 $$|a-b| < 0.001$$。正确答案是 B。
2. 分组检测的过程是二分法的应用:
- 第一次检测16人分两组,确定8人组;
- 第二次检测8人分两组,确定4人组;
- 第三次检测4人分两组,确定2人组;
- 第四次检测2人分两组,确定感染者。
总共需要 4 次检测,正确答案是 B。
4. 二分法要求函数在区间内连续且变号:
- A选项 $$f(x)=x^4$$ 无零点且不变号;
- B选项 $$f(x)=\tan x +2$$ 在 $$(-\pi/2, \pi/2)$$ 内单调递增且无零点;
- C选项 $$f(x)=\cos x -1$$ 零点为 $$2k\pi$$,但导数在零点处为0,二分法可能失效;
- D选项 $$f(x)=|2^x-3|$$ 在 $$x=\log_2 3$$ 处有零点且变号,可用二分法。
正确答案是 D。
5. 设 $$f(x)=\lg x +x-3$$,计算区间端点函数值:
- $$f(2)=\lg 2+2-3 \approx -0.3$$;
- $$f(3)=\lg 3+3-3 \approx 0.48$$。
$$f(2)f(3)<0$$,故零点在 $$(2,3)$$,正确答案是 C。
6. 设 $$f(x)=\ln x +x-4$$,计算表格中区间端点函数值:
- $$f(2)=\ln 2+2-4 \approx -1.31$$;
- $$f(3)=\ln 3+3-4 \approx 0.10$$。
$$f(2)f(3)<0$$,故零点在 $$(2,3)$$,正确答案是 C。
7. 根据二分法数据:
- $$f(2.25)=-0.0119$$,$$f(2.375)=0.1624$$;
- 继续二分到 $$f(2.28125)\approx 0.0319$$,此时区间长度为 $$0.1$$,近似根为 $$2.2$$。
正确答案是 B。
8. 二分法要求函数连续且与x轴有交点:
- A选项函数不连续;
- B选项函数与x轴无交点;
- C选项函数连续且有交点,可用二分法;
- D选项函数与x轴相切,二分法可能失效。
正确答案是 C。
9. 初始区间长度为1,每次二分后区间长度减半。要求精度为0.01,需满足 $$\frac{1}{2^n} < 0.01$$,解得 $$n \geq 7$$。
至少需要 7 次计算,正确答案是 C。
10. 分析各说法:
- ①正确,$$(x_0,0)$$是零点;
- ②错误,二分法还需函数连续且变号;
- ③错误,方程的根就是函数的零点;
- ④错误,二分法可能得到精确值。
只有1个说法正确,正确答案是 B。
.jpg)