正确率60.0%如图,函数$${{f}{(}{x}{)}}$$的图像与$${{x}}$$轴交于$$M ( x_{1}, ~ 0 ), ~ N ( x_{2}, ~ 0 ),$$$$P ( x_{3}, ~ 0 ), ~ Q ( x_{4}, ~ 0 )$$四点,则不能用二分法求出的$${{f}{(}{x}{)}}$$的零点是()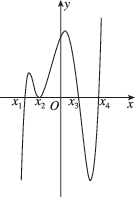
B
A.$${{x}_{1}}$$
B.$${{x}_{2}}$$
C.$${{x}_{3}}$$
D.$${{x}_{4}}$$
2、['二分法的定义', '函数零点所在区间的判定']正确率80.0%如图是函数$${{f}{(}{x}{)}}$$的图像,它与$${{x}}$$轴有$${{4}}$$个不同的交点,给出的下列四个区间之中,存在不能用二分法求的零点,则该零点所在的区间是()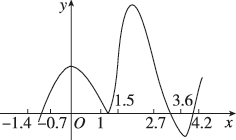
B
A.$$(-1. 4, ~-0. 7 )$$
B.$$( 1, 1. 5 )$$
C.$$( 2. 7, 3. 6 )$$
D.$$( 3. 6, 4. 2 )$$
3、['二分法的定义', '函数零点存在定理']正确率40.0%已知$${{f}{(}{x}{)}}$$是定义在$$( 0,+\infty)$$上的单调函数,且对任意的$$x \in( 0,+\infty)$$,都有$$f [ f ( x )-\operatorname{l o g}_{2} x ]=1$$,则方程$$f ( x )-f^{\prime} ( x )=1 ( f^{\prime} ( x )$$为函数$${{f}{(}{x}{)}}$$的导函数)的解所在的区间是
C
A.$$( 0, \frac{1} {2} )$$
B.$$( \frac{1} {2}, 0 )$$
C.$$( 1, 2 )$$
D.$$( 2, 3 )$$
4、['二分法的定义', '函数零点存在定理']正确率60.0%对于函数$${{f}{(}{x}{)}}$$在定义域内用二分法的求解过程中得到$$f ~ ( \ 2 0 1 4 ) ~ < 0, ~ f ~ ( \ 2 0 1 5 ) ~ < 0, ~ f ~ ( \ 2 0 1 6 ) ~ > 0$$,则下述描述正确的是()
D
A.函数$${{f}{(}{x}{)}}$$在$$( \ 2 0 1 4, \ 2 0 1 5 )$$内不存在零点
B.函数$${{f}{(}{x}{)}}$$在$$( \ 2 0 1 5, \ 2 0 1 6 )$$内不存在零点
C.函数$${{f}{(}{x}{)}}$$在$$( \ 2 0 1 5, \ 2 0 1 6 )$$内存在零点,并且仅有一个
D.函数$${{f}{(}{x}{)}}$$在$$( \ 2 0 1 4, \ 2 0 1 5 )$$内可能存在零点
5、['二分法的定义', '用二分法求函数零点的近似值']正确率60.0%用二分法研究函数$$f ( x )=x^{5}+8 x^{3}-1$$的零点时,第一次经过计算$$f ( 0 ) < 0, \; \; f ( 0. 5 ) > 0$$,< 0,f(0.5) >$${{0}}$$,则其中一个零点所在的区间和第二次应计算的函数值分别为()
D
A.$$( 0, 0. 5 ), \; \, f ( 0. 1 2 5 )$$
B.$$( 0. 5, 1 ), ~ f ( 0. 2 5 )$$
C.$$( 0. 5, 1 ), ~ f ( 0. 7 5 )$$
D.$$( 0, 0. 5 ), ~ \, f ( 0. 2 5 )$$
6、['二分法的定义', '用二分法求函数零点的近似值', '函数零点存在定理']正确率60.0%函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=2^{x} ~-5$$的零点在下列哪个区间内()
C
A.$$( {\bf0}, \mathrm{\bf~ 1} )$$
B.$$( 1, \ 2 )$$
C.$$( 2, \ 3 )$$
D.$$( 3, \ 4 )$$
7、['二分法的定义']正确率60.0%下列函数图像与$${{x}}$$轴均有交点,但不宜用二分法求交点横坐标的是$${{(}{)}}$$
B
A.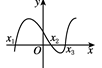
B.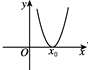
C.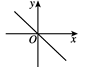
D.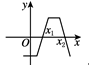
正确率60.0%用二分法求函数$$f \left( x \right)=x^{3}+5$$的零点,可以取的初始区间是()
A
A.$$(-2, 1 )$$
B.$$(-1, 0 )$$
C.$$( 0, 1 )$$
D.$$( 1, 2 )$$
9、['二分法的定义', '用二分法求函数零点的近似值']正确率60.0%已知$${{f}{(}{x}{)}}$$的一个零点$$x_{0} \in( 2, 3 ),$$用二分法求精确度为$${{0}{.}{0}{1}}$$的$${{x}_{0}}$$的近似值时,判断各区间中点的函数值的符号最多需要的次数为()
B
A.$${{6}}$$
B.$${{7}}$$
C.$${{8}}$$
D.$${{9}}$$
10、['函数零点所在区间的判定', '二分法的定义', '函数零点存在定理']正确率60.0%若函数$${{f}{(}{x}{)}}$$在$${{[}{a}}$$,$${{b}{]}}$$上的图象为一条连续不断的曲线,且同时满足$$f ( a ) \cdot f ( b ) < ~ 0$$,$$f ( a ) \cdot f \left( \frac{a+b} {2} \right) > 0$$,则()
B
A.$${{f}{(}{x}{)}}$$在$$\left[ a, \frac{a+b} {2} \right]$$上有零点
B.$${{f}{(}{x}{)}}$$在$$\left[ \frac{a+b} {2}, b \right]$$上有零点
C.$${{f}{(}{x}{)}}$$在$$\left[ a, \frac{a+b} {2} \right]$$上无零点
D.$${{f}{(}{x}{)}}$$在$$\left[ \frac{a+b} {2}, b \right]$$上无零点
1. 解析:二分法要求函数在零点附近单调且穿过x轴。观察图像,$$x_1$$和$$x_4$$处函数单调穿过x轴,适合二分法;$$x_2$$和$$x_3$$处函数与x轴相切,不穿过x轴,无法用二分法。但题目问的是“不能用二分法”的零点,而$$x_3$$处函数值不变号,因此选C。
2. 解析:二分法要求函数在区间内单调且穿过x轴。观察图像,区间$$(2.7,3.6)$$内函数与x轴相切(不变号),无法用二分法,故选C。
3. 解析:由题意,$$f(x)$$单调且$$f(f(x)-\log_2 x)=1$$,设$$f(x)-\log_2 x = C$$(常数),则$$f(C)=1$$。因为$$f(x)$$单调,$$C$$唯一。令$$x=C$$,得$$f(C)-\log_2 C=C$$,即$$1-\log_2 C=C$$。解得$$C=1$$(验证成立),故$$f(x)=1+\log_2 x$$。求导得$$f'(x)=\frac{1}{x \ln 2}$$,方程$$f(x)-f'(x)=1$$化为$$\log_2 x - \frac{1}{x \ln 2}=0$$。令$$g(x)=\log_2 x - \frac{1}{x \ln 2}$$,计算$$g(1)=-1$$,$$g(2)=1-\frac{1}{2 \ln 2}>0$$,零点在$$(1,2)$$,选C。
4. 解析:由$$f(2015)<0$$和$$f(2016)>0$$,根据介值定理,$$(2015,2016)$$内至少有一个零点。但$$f(2014)<0$$和$$f(2015)<0$$无法确定$$(2014,2015)$$是否有零点,可能无也可能有(如函数先下降再上升)。故选D。
5. 解析:由$$f(0)<0$$和$$f(0.5)>0$$,零点在$$(0,0.5)$$。第二次取中点$$0.25$$,计算$$f(0.25)$$,故选D。
6. 解析:计算$$f(2)=2^2-5=-1$$,$$f(3)=2^3-5=3$$,由介值定理,零点在$$(2,3)$$,选C。
7. 解析:二分法要求函数穿过x轴(变号)。选项B的图像与x轴相切(不变号),不宜用二分法,故选B。
8. 解析:计算$$f(-2)=(-2)^3+5=-3$$,$$f(1)=1^3+5=6$$,满足$$f(-2)\cdot f(1)<0$$,可选A。
9. 解析:初始区间长度为1,每次二分后长度减半。要求精度$$0.01$$,需满足$$\frac{1}{2^n}<0.01$$,解得$$n \geq 7$$,故选B。
10. 解析:由$$f(a)\cdot f(b)<0$$和$$f(a)\cdot f\left(\frac{a+b}{2}\right)>0$$,得$$f\left(\frac{a+b}{2}\right)$$与$$f(a)$$同号,故零点在$$\left(\frac{a+b}{2}, b\right)$$,选B。
.jpg)