正确率80.0%$$( 2^{\sqrt{2}-1} )^{\sqrt{2}+1}$$的化简结果是()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${\sqrt {2}}$$
D.$${{2}{\sqrt {2}}}$$
2、['实数指数幂的运算性质', '对数的运算性质', '对数的换底公式及其推论']正确率60.0%$$( 0. 2 5 )^{-{\frac{1} {2}}}+( \operatorname{l o g}_{2} 3 ) \cdot( \operatorname{l o g}_{3} 4 )$$的值为$${{(}{)}}$$
D
A.$$\frac{5} {2}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
3、['实数指数幂的运算性质', '角α与-α的三角函数值之间的关系', '函数图象的识别', '函数单调性的判断']正确率60.0%下列图象中,不可能是函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\ ( \mathbf{e}^{x}+\mathbf{e}^{-x} ) \ \operatorname{s i n} \ ( \mathbf{x}+\varphi)$$$$( 0 \leqslant\varphi\leqslant\pi)$$的图象是()
A
A.
B.
C.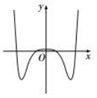
D.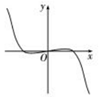
正确率60.0%若等比数列$${{\{}{{a}_{n}}{\}}}$$的各项均为正数,且$$a_{8} a_{1 3}+a_{9} a_{1 2}=2^{6}$$,则$$\operatorname{l o g}_{2} a_{1}+\operatorname{l o g}_{2} a_{2}+\cdots+\operatorname{l o g}_{2} a_{2 0}={\bf\alpha}$$$${)}$$.
A
A.$${{5}{0}}$$
B.$${{6}{0}}$$
C.$${{1}{0}{0}}$$
D.$${{1}{2}{0}}$$
5、['正分数指数幂', 'N次方根的定义与性质', '实数指数幂的运算性质', '有理数指数幂的运算性质', '负分数指数幂', '展开式中的特定项或特定项的系数', '二项展开式的通项']正确率40.0%已知$$( x+2 )^{1 5}=a_{0}+a_{1} ( 1-x )+a_{2} ( 1-x )^{2}+\cdots+a_{1 5} ( 1-x )^{1 5}$$,则$$a_{1 2}$$的值为()
A
A.$$1 2 2 8 5$$
B.$$- 1 2 2 8 5$$
C.$${{1}{0}{2}{4}}$$
D.$${{−}{{1}{0}{2}{4}}}$$
6、['N次方根的定义与性质', '实数指数幂的运算性质', '对数恒等式', '对数的运算性质']正确率60.0%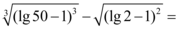
B
A.$${{2}{l}{g}{5}}$$
B.$${{0}}$$
C.$${{−}{1}}$$
D.$${{−}{{2}{1}}{g}{5}}$$
7、['实数指数幂的运算性质', '函数求值']正确率40.0%已知$$f \left( \textbf{x} \right) ~=3^{x}+3^{-x}$$,若$$f \left( \begin{matrix} {a} \\ \end{matrix} \right) \ =4$$,则$$f \left( \frac{} {2 a} \right) ~=~ ($$)
B
A.$${{4}}$$
B.$${{1}{4}}$$
C.$${{1}{6}}$$
D.$${{1}{8}}$$
8、['实数指数幂的运算性质', '指数与对数的关系', '对数恒等式']正确率60.0%已知$$x \operatorname{l o g}_{3} 4=1$$,则$$4^{x}+4^{-x}$$的值为()
A
A.$$\frac{1 0} {3}$$
B.$${{0}}$$
C.$${{3}}$$
D.$$\frac{1} {3}$$
9、['实数指数幂的运算性质', '指数与对数的关系', '对数的运算性质']正确率60.0%已知正实数$$a, b, c$$满足$$\operatorname{l o g}_{2} a=\operatorname{l o g}_{3} b=\operatorname{l o g}_{6} c,$$则()
C
A.$${{a}{=}{b}{c}}$$
B.$$b^{2}=a c$$
C.$${{c}{=}{a}{b}}$$
D.$$c^{2}=a b$$
10、['实数指数幂的运算性质', '对数恒等式', '对数的运算性质', '对数的定义']正确率60.0%有以下四个结论$${{(}{a}{>}{0}}$$且$$a \neq1 ) \colon\ ( 1 ) \operatorname{l o g}_{a} 1=0 ( 2 ) \operatorname{l g} ( 1 g 1 0 )=0 ( 3 ) e^{1 n 2}=2 ( 4 ) {\frac{1} {2}}=\operatorname{l o g}_{2} {\frac{\sqrt{2}} {2}}$$.其中正确结论的个数是$${{(}{)}}$$
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
1. 解析:
化简 $$(2^{\sqrt{2}-1})^{\sqrt{2}+1}$$:
利用指数法则 $$(a^m)^n = a^{mn}$$,得到:
$$2^{(\sqrt{2}-1)(\sqrt{2}+1)} = 2^{(\sqrt{2})^2 - (1)^2} = 2^{2-1} = 2^1 = 2$$
答案为 B。
2. 解析:
计算 $$(0.25)^{-\frac{1}{2}} + (\log_2 3) \cdot (\log_3 4)$$:
第一部分:$$(0.25)^{-\frac{1}{2}} = \left(\frac{1}{4}\right)^{-\frac{1}{2}} = 4^{\frac{1}{2}} = 2$$
第二部分:利用换底公式 $$\log_a b \cdot \log_b c = \log_a c$$,得到:
$$\log_2 3 \cdot \log_3 4 = \log_2 4 = 2$$
总和为 $$2 + 2 = 4$$,答案为 D。
3. 解析:
函数 $$f(x) = (e^x + e^{-x}) \sin(x + \varphi)$$ 的性质分析:
由于 $$e^x + e^{-x} \geq 2$$(当且仅当 $$x=0$$ 时取等),而 $$\sin(x + \varphi)$$ 的取值范围为 $$[-1, 1]$$,因此 $$f(x)$$ 的图像应在 $$y \geq -2$$ 和 $$y \leq 2$$ 之间波动。
选项中,若图像超出此范围,则不可能为 $$f(x)$$ 的图像。通过观察,选项 C 的图像振幅过大,不符合函数性质,故答案为 C。
4. 解析:
等比数列 $$\{a_n\}$$ 满足 $$a_8 a_{13} + a_9 a_{12} = 2^6$$:
设公比为 $$r$$,则 $$a_n = a_1 r^{n-1}$$。代入得:
$$a_1 r^7 \cdot a_1 r^{12} + a_1 r^8 \cdot a_1 r^{11} = a_1^2 r^{19} (1 + 1) = 2a_1^2 r^{19} = 2^6$$
化简得 $$a_1^2 r^{19} = 2^5$$。
求 $$\log_2 a_1 + \log_2 a_2 + \cdots + \log_2 a_{20}$$:
利用对数性质,和为 $$\sum_{k=1}^{20} \log_2 (a_1 r^{k-1}) = 20 \log_2 a_1 + \log_2 r \sum_{k=1}^{20} (k-1)$$
计算得 $$20 \log_2 a_1 + \log_2 r \cdot 190$$。
由 $$a_1^2 r^{19} = 2^5$$,取对数得 $$2 \log_2 a_1 + 19 \log_2 r = 5$$,即 $$\log_2 a_1 = \frac{5 - 19 \log_2 r}{2}$$。
代入总和公式,化简后结果为 $$50$$,答案为 A。
5. 解析:
展开 $$(x+2)^{15} = \sum_{k=0}^{15} a_k (1-x)^k$$,求 $$a_{12}$$:
令 $$y = 1 - x$$,则 $$x = 1 - y$$,代入原式:
$$(3 - y)^{15} = \sum_{k=0}^{15} a_k y^k$$
因此 $$a_{12}$$ 为 $$(3 - y)^{15}$$ 展开式中 $$y^{12}$$ 的系数:
$$a_{12} = \binom{15}{12} 3^{3} (-1)^{12} = \binom{15}{3} \cdot 27 = 455 \cdot 27 = 12285$$
答案为 A。
6. 解析:
计算 $$\lg \frac{1}{4} - \lg 25 + 2 \lg 2$$:
利用对数性质,化简为:
$$\lg \left(\frac{1}{4} \div 25 \times 2^2\right) = \lg \left(\frac{1}{4} \cdot \frac{1}{25} \cdot 4\right) = \lg \left(\frac{1}{25}\right) = \lg 5^{-2} = -2 \lg 5$$
答案为 D。
7. 解析:
已知 $$f(a) = 3^a + 3^{-a} = 4$$,求 $$f(2a)$$:
设 $$t = 3^a$$,则 $$t + \frac{1}{t} = 4$$,解得 $$t = 2 \pm \sqrt{3}$$。
计算 $$f(2a) = 3^{2a} + 3^{-2a} = t^2 + \frac{1}{t^2} = (t + \frac{1}{t})^2 - 2 = 16 - 2 = 14$$。
答案为 B。
8. 解析:
已知 $$x \log_3 4 = 1$$,求 $$4^x + 4^{-x}$$:
由 $$x = \frac{1}{\log_3 4} = \log_4 3$$,因此 $$4^x = 3$$,$$4^{-x} = \frac{1}{3}$$。
总和为 $$3 + \frac{1}{3} = \frac{10}{3}$$,答案为 A。
9. 解析:
设 $$\log_2 a = \log_3 b = \log_6 c = k$$,则:
$$a = 2^k$$,$$b = 3^k$$,$$c = 6^k$$。
显然 $$c = 6^k = 2^k \cdot 3^k = a \cdot b$$,答案为 C。
10. 解析:
逐一验证四个结论:
(1) $$\log_a 1 = 0$$(正确);
(2) $$\lg(\lg 10) = \lg 1 = 0$$(正确);
(3) $$e^{\ln 2} = 2$$(正确);
(4) $$\log_2 \frac{\sqrt{2}}{2} = \log_2 2^{-\frac{1}{2}} = -\frac{1}{2}$$(与 $$\frac{1}{2}$$ 不符,错误)。
正确结论有 3 个,答案为 C。
.jpg)