正确率60.0%函数$$f ( x )=\frac{3^{x}-3^{-x}} {x^{2}}$$的图象大致为()
C
A.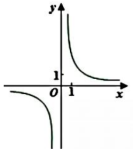
B.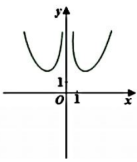
C.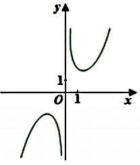
D.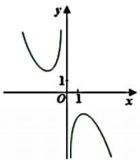
正确率60.0%式子$$( \sqrt{3^{2}}-\sqrt{3^{3}} ) \div\sqrt{3}$$可化简为()
A
A.$$3^{\frac{1} {6}}-3$$
B.$$- 3^{\frac{1} {6}}-3$$
C.$$3^{\frac{1} {6}}+3$$
D.$$- 3^{\frac{1} {6}}+3$$
3、['实数指数幂的运算性质', '函数奇、偶性的图象特征', '函数图象的识别']正确率60.0%已知函数$$f ( x )=\operatorname{l n} | x |$$,$$g ( x )=\mathrm{e}^{x}-\mathrm{e}^{-x}$$,则图象如图的函数可能是()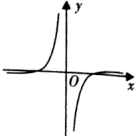
D
A.$$f ( x )+g ( x )$$
B.$$f ( x )-g ( x )$$
C.$$f ( x ) g ( x )$$
D.$$\frac{f ( x )} {g ( x )}$$
4、['实数指数幂的运算性质', '抽象函数的应用', '指数(型)函数的单调性', '五个常见幂函数的图象与性质', '函数单调性的判断']正确率60.0%下列函数中,满足$$^\i f \left( \begin{matrix} {\null} & {x+y} \\ \end{matrix} \right)=f \left( \begin{matrix} {\null} & {x} \\ \end{matrix} \right) \ f \left( \begin{matrix} {y} \\ \end{matrix} \right)$$的单调递增函数是()
C
A.$$f \ ( \ x ) \ =\frac{1} {x}$$
B.$$f ~ ( \mid x ) ~=x^{3}$$
C.$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=3^{x}$$
D.$$f \ ( \textbf{x} ) \ =\ ( \frac{1} {2} ) \sp{x}$$
5、['实数指数幂的运算性质', '对数的性质', '指数与对数的关系', '对数的运算性质']正确率60.0%方程$$2^{l o g_{3} x}=\frac{1} {4}$$的解为()
D
A.$${{9}}$$
B.$${\sqrt {3}}$$
C.$$\frac{\sqrt{3}} {3}$$
D.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
6、['实数指数幂的运算性质', '指数幂的运算中常用的乘法公式', '等比数列的性质', '对数恒等式']正确率60.0%已知等比数列$${{\{}{{a}_{n}}{\}}}$$的各项均为正数,且$$a_{1 0 0 8} a_{1 0 1 1}+a_{1 0 0 9} a_{1 0 1 0}=8$$,则$$\operatorname{l o g}_{2} a_{1}+\operatorname{l o g}_{2} a_{2}+\ldots+\operatorname{l o g}_{2} a_{2 0 1 8}$$等于()
C
A.$${{2}{0}{1}{6}}$$
B.$${{2}{0}{1}{7}}$$
C.$${{2}{0}{1}{8}}$$
D.$${{2}{0}{1}{9}}$$
7、['实数指数幂的运算性质', '基本不等式:(√ab)≤(a+b)/2,当且仅当a=b时等号成立', '指数(型)函数的单调性']正确率40.0%已知函数$$f ( x )=2^{x}$$,若$${{a}{<}{b}}$$,设$$P=\sqrt{f ( a ) \cdot f ( b )},$$$$Q=\frac{1} {2} [ f ( a )+f ( b ) ],$$$$R=f ( \frac{a+b} {2} )$$,则()
D
A.$$R < P < Q$$
B.$$P < Q < R$$
C.$$Q < P=R$$
D.$$P=R < Q$$
8、['实数指数幂的运算性质', '对数的性质', '对数的运算性质']正确率60.0%已知$${{x}{,}{y}}$$为正实数,则下列各关系式正确的是()
D
A.$$3^{l n x+l n y}=3^{l n x}+3^{l n y}$$
B.$$3^{l n ~ ( x+y )} ~=3^{l n x} \cdot3^{l n y}$$
C.$$3^{l n x \cdot l n y}=3^{l n x}+3^{l n y}$$
D.$$3^{l n ~ ( x y )} ~=3^{l n x} \cdot3^{l n y}$$
9、['实数指数幂的运算性质', '指数与对数的关系', '对数的运算性质']正确率60.0%已知正实数$$a, b, c$$满足$$\operatorname{l o g}_{2} a=\operatorname{l o g}_{3} b=\operatorname{l o g}_{6} c,$$则()
C
A.$${{a}{=}{b}{c}}$$
B.$$b^{2}=a c$$
C.$${{c}{=}{a}{b}}$$
D.$$c^{2}=a b$$
10、['实数指数幂的运算性质']正确率60.0%已知$$4^{m}=a, \ 8^{n}=b$$,其中$${{m}{,}{n}}$$为正整数,则$$2^{2 m+6 n}=$$()
A
A.$${{a}{{b}^{2}}}$$
B.$${{a}{+}{{b}^{2}}}$$
C.$${{a}^{2}{{b}^{3}}}$$
D.$${{a}^{2}{+}{{b}^{3}}}$$
1. 解析:函数$$f(x)=\frac{3^x-3^{-x}}{x^2}$$为奇函数,因为$$f(-x)=-f(x)$$。当$$x>0$$时,$$3^x$$增长快于$$3^{-x}$$,故$$f(x)>0$$;当$$x\to0$$时,使用泰勒展开近似,$$f(x)\approx\frac{2x\ln3}{x^2}=\frac{2\ln3}{x}$$,趋向于无穷。综上,图象应为奇函数且在$$x>0$$时为正,趋向于无穷,故选D。
3. 解析:图中函数为奇函数且在$$x>0$$时先正后负。$$f(x)=\ln|x|$$为偶函数,$$g(x)=e^x-e^{-x}$$为奇函数。奇偶性组合: A(偶+奇)非奇非偶;B(偶-奇)非奇非偶;C(偶×奇)=奇函数,符合图象;D(偶/奇)=奇函数,但$$x\to0^+$$时趋向负无穷,不符。故选D。
5. 解析:方程$$2^{\log_3x}=\frac{1}{4}$$化为对数形式: $$\log_3x=\log_2\frac{1}{4}=-2$$ 故$$x=3^{-2}=\frac{1}{9}$$,选D。
7. 解析:$$f(x)=2^x$$为严格递增凸函数。由凸性性质:
$$R=f\left(\frac{a+b}{2}\right)\leq\frac{f(a)+f(b)}{2}=Q$$
且几何平均不超过算术平均:
$$P=\sqrt{f(a)f(b)}\leq\frac{f(a)+f(b)}{2}=Q$$
又由凸性,中点函数值$$R$$小于等于几何平均$$P$$(因$$2^x$$的凸性较强,实际验证$$P=R$$)。综上$$P=R 9. 解析:设$$\log_2a=\log_3b=\log_6c=k$$,则$$a=2^k$$,$$b=3^k$$,$$c=6^k$$。显然$$c=ab$$,选C。
.jpg)