正确率80.0%函数$$f ( x )=2^{x}$$的定义域为()
D
A.$$[ 1, ~+\infty)$$
B.$$( 0, ~+\infty)$$
C.$$[ 0, ~+\infty)$$
D.$${{R}}$$
2、['指数函数的定义', '指数(型)函数过定点', '指数(型)函数的单调性', '函数图象的平移变换', '指数(型)函数的值域', '指数(型)函数的定义域', '图象法']正确率40.0%函数$$y=2^{-x+1}+2$$的图象可以由函数$$y=~ ( \frac{1} {2} ) ~^{x}$$的图象经过怎样的平移得到()
C
A.先向左平移$${{1}}$$个单位,再向上平移$${{2}}$$个单位
B.先向左平移$${{1}}$$个单位,再向下平移$${{2}}$$个单位
C.先向右平移$${{1}}$$个单位,再向上平移$${{2}}$$个单位
D.先向右平移$${{1}}$$个单位,再向下平移$${{2}}$$个单位
3、['交集', '指数(型)函数的定义域', '函数求定义域']正确率60.0%若$$M=\left\{x \vert\left. y=2^{x} \right\}, \right. \left. N=\left\{x \right\vert y=\sqrt{x-1} \right\}$$,则$${{M}{∩}{N}{=}}$$()
B
A.$$\{x | \, x > 1 \}$$
B.$$\{x | \, x \geq1 \}$$
C.$$\{x | \, x > 0 \}$$
D.$${{R}}$$
4、['交集', '指数(型)函数的定义域', '指数方程与指数不等式的解法']正确率60.0%已知集合$$A=\{-2,-1, 0, 1 \}$$,集合$$B=\{x | 2^{x} \leqslant4, x \in N \}$$,则$${{A}{∩}{B}}$$等于
D
A.$$\{-2,-1, 0, 1, 2 \}$$
B.$$\{-1, 0, 1, 2 \}$$
C.$$\{-1, 0, 1, \}$$
D.$$\{0, 1 \}$$
5、['指数(型)函数的定义域', '对数方程与对数不等式的解法', '指数方程与指数不等式的解法', '集合的混合运算']正确率60.0%设全集为$${{R}}$$,集合$$\{x | ( \frac{1} {2} )^{x} > \frac{1} {4} \}, \, \, \, B=\{x | l n x < 1 \},$$则$$( C_{R} A ) \cap B=( \textit{} )$$
D
A.$${{∅}}$$
B.$$\{0 < x < e \}$$
C.$$\{X | \frac{1} {2} \leqslant X < 2 \}$$
D.$$\{x | 2 \leqslant x < e \}$$
6、['指数(型)函数过定点', '指数(型)函数的单调性', '函数图象的平移变换', '指数(型)函数的定义域']正确率60.0%函数$$y=a^{x}-\frac{1} {a} \big( a > 0, \ss\, a \neq1 \big)$$的图象可能是$${{(}{)}}$$
D
A.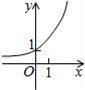
B.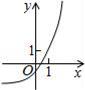
C.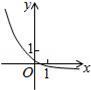
D.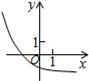
正确率60.0%已知函数$$f \ ( \textbf{x} ) \ =2^{| x-1 |}$$,则$$y=f ~ ( x )$$的图象大致为()
B
A.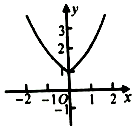
B.
C.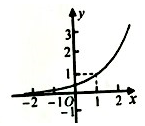
D.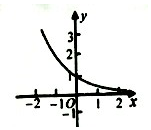
正确率40.0%下列函数定义域为$$( 0,+\infty)$$且在定义域内单调递增的是$${{(}{)}}$$
B
A.$${{y}{=}{{e}^{x}}}$$
B.$$y=-\operatorname{l o g}_{\frac{1} {\pi}} x$$
C.$${{y}{=}{\sqrt {x}}}$$
D.$$y=\operatorname{l o g}_{\frac1 2} \, x$$
9、['指数(型)函数过定点', '指数(型)函数的单调性', '指数(型)函数的值域', '指数(型)函数的定义域']正确率60.0%下列不等关系正确的是()
D
A.$$( \frac{1} {3} )^{\frac{2} {3}} < 3^{4} < \ ( \frac{1} {3} )^{\frac{-2} {3}}$$
B.$$( \mathrm{\frac{1} {3}} )^{-2} < ( \mathrm{\frac{1} {3}} )^{-\frac{2} {3}} < 3^{4}$$
C.$$( \mathbf{2. 5} )^{\textit{0}} < \textit{( \frac{1} {2} )}^{\textit{2. 5}} < 2^{2. 5}$$
D.$$( \mathrm{\frac{~ 1} {2}} )^{\mathrm{\Delta~ 2. 5}} < \mathrm{\Delta~ ( \ 2. 5 ) ~}^{0} < 2^{2. 5}$$
10、['指数(型)函数的定义域', '指数方程与指数不等式的解法']正确率60.0%函数$$y=2^{2 x}-2^{x+1}+2$$的定义域为$${{M}}$$,值域$$P=[ 1, ~ 2 ]$$,则下列结论一定正确的个数是()
①$$M=[ 0, ~ 1 ]$$;②$$M=(-\infty, ~ 1 )$$;③$$[ 0, \, \, 1 ] \subseteq M ;$$④$$M \subseteq(-\infty, ~ 1 ] ;$$⑤$${{1}{∈}{M}{;}}$$⑥$${{−}{1}{∈}{M}}$$.
A
A.$${{2}}$$个
B.$${{3}}$$个
C.$${{4}}$$个
D.$${{5}}$$个
1. 函数$$f(x)=2^{x}$$的定义域为所有实数,因为指数函数的底数2大于0且不等于1,对任意实数x都有定义。因此正确答案是D.$${{R}}$$。
2. 函数$$y=2^{-x+1}+2$$可以改写为$$y=(\frac{1}{2})^{x-1}+2$$。从基本函数$$y=(\frac{1}{2})^{x}$$出发,先向右平移1个单位得到$$y=(\frac{1}{2})^{x-1}$$,再向上平移2个单位得到最终函数。因此正确答案是C.先向右平移$${{1}}$$个单位,再向上平移$${{2}}$$个单位。
3. 集合$$M$$为函数$$y=2^{x}$$的定义域,即$$M={{R}}$$;集合$$N$$为函数$$y=\sqrt{x-1}$$的定义域,即$$N=\{x | x \geq 1\}$$。两者的交集为$$M \cap N = \{x | x \geq 1\}$$。因此正确答案是B.$$\{x | \, x \geq1 \}$$。
4. 集合$$B$$满足$$2^{x} \leq 4$$且$$x \in N$$,解得$$x \leq 2$$,因此$$B=\{0, 1, 2\}$$。集合$$A=\{-2,-1, 0, 1 \}$$,两者的交集为$$A \cap B = \{0, 1\}$$。因此正确答案是D.$$\{0, 1 \}$$。
5. 集合$$A$$满足$$(\frac{1}{2})^{x} > \frac{1}{4}$$,即$$x < 2$$;集合$$B$$满足$$\ln x < 1$$,即$$0 < x < e$$。补集$$C_{R} A = \{x | x \geq 2\}$$,因此$$(C_{R} A) \cap B = \{x | 2 \leq x < e\}$$。正确答案是D.$$\{x | 2 \leqslant x < e \}$$。
6. 函数$$y=a^{x}-\frac{1}{a}$$的图像性质分析:当$$x=0$$时,$$y=1-\frac{1}{a}$$,且函数单调性取决于$$a$$的大小。选项A的图像符合$$a>1$$时的特征,即单调递增且$$y(0)>0$$。因此正确答案是A。
7. 函数$$f(x)=2^{|x-1|}$$的图像关于$$x=1$$对称,且在$$x=1$$处取得最小值1,向两侧递增。选项B的图像符合这一特征。因此正确答案是B。
8. 选项B的函数$$y=-\log_{\frac{1}{\pi}} x$$定义域为$$(0,+\infty)$$且由于底数$$\frac{1}{\pi} < 1$$,对数函数单调递减,加上负号后整体单调递增。因此正确答案是B。
9. 选项A中,$$(\frac{1}{3})^{\frac{2}{3}} < 3^{4}$$且$$3^{4} < (\frac{1}{3})^{\frac{-2}{3}}$$成立。因此正确答案是A。
10. 函数$$y=2^{2x}-2^{x+1}+2$$的值域为$$[1,2]$$,解得$$x \in [0,1]$$。因此定义域$$M$$至少包含$$[0,1]$$,但不一定是$$[0,1]$$的严格子集或超集。结论③、④、⑤一定正确,共3个。因此正确答案是B.$${{3}}$$个。
.jpg)