正确率80.0%下列函数中,指数函数的个数为()
①$$y=\left( \frac{1} {2} \right)^{x-1}$$; ②$$y=m^{x} ( m > 0$$且$${{m}{≠}{1}{)}}$$;③$$y=1^{x} \left( x \in\mathbf{R} \right)$$;④ $$y=\left( \frac{1} {2} \right)^{2 x}-1 ( x > 1 )$$ .
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
2、['指数函数的定义', '指数(型)函数过定点']正确率80.0%下列各点中,在函数$$f ( x )=2^{x}-1$$的图像上的是()
A
A.$$( 0, \ 0 )$$
B.$$( 0, \ 1 )$$
C.$$( 1, \ 0 )$$
D.$$( 1, ~ 2 )$$
3、['指数函数的定义']正确率80.0%已知函数$$y=( a+2 )^{x}$$是指数函数,则实数$${{a}}$$的取值范围是()
C
A.$$(-2,+\infty)$$
B.$$[-2,+\infty)$$
C.$$(-2, ~-1 ) \cup(-1, ~+\infty)$$
D.$$( 1, 2 ) \cup( 2,+\infty)$$
4、['指数函数的定义']正确率80.0%若指数函数$${{f}{(}{x}{)}}$$的图像过点$$( 3, 8 ),$$则$${{f}{(}{x}{)}}$$的解析式为()
B
A.$$f ( x )=x^{3}$$
B. $$f ( x )=2^{x}$$
C.$$f ( x )=\left( \frac{1} {2} \right)^{x}$$
D.$$f ( x )=x^{\frac{1} {3}}$$
5、['指数函数的定义', '一次函数的图象与直线的方程', '根据函数零点个数求参数范围', '分段函数模型的应用', '对数的定义']正确率40.0%已知函数$$f ( x )=\left\{\begin{matrix} {\mathrm{e}^{x},} & {x \leqslant0,} \\ {\mathrm{l n} \, x,} & {x > 0,} \\ \end{matrix} \right.$$$$g ( x )=f ( x )+x+a$$.若$${{g}{(}{x}{)}}$$存在$${{2}}$$个零点,则$${{a}}$$的取值范围是()
C
A.$${{[}{–}{1}}$$,$${{0}}$$)
B.$${{[}{0}}$$,$${{+}{∞}}$$)
C.$${{[}{–}{1}}$$,$${{+}{∞}}$$)
D.$${{[}{1}}$$,$${{+}{∞}}$$)
6、['指数函数的定义', '一元二次方程的解集']正确率80.0%函数$$y=( 2 a^{2}-3 a+2 ) a^{x}$$是指数函数,则$${{a}}$$的取值范围是()
C
A.$$a > 0, a \neq1$$
B.$${{a}{=}{1}}$$
C.$$a=\frac{1} {2}$$
D.
正确率80.0%函数$$f ( x )=a^{x} ( a > 0,$$且$${{a}{≠}{1}{)}}$$的图象经过点$$P ( 3, 2 7 )$$,则$$f ( 2 )=( \textsubscript{\Pi} )$$
A.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{1} {3}$$
D.$${{9}}$$
8、['指数函数的定义']正确率60.0%指数函数$${{y}{=}{{a}^{x}}}$$的图象经过点$$( 3, \ 2 7 )$$,则$${{a}}$$的值是()
A
A.$${{3}}$$
B.$${{9}}$$
C.$$\frac{1} {3}$$
D.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
9、['指数函数的定义', '函数图象的识别']正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=a \cdot2^{x}-1$$与函数$$g \ ( \textup{x} ) \ =x^{3}+a x^{2}+1 \ ( \textup{a} \in R )$$,下列选项中不可能是函数$${{f}{(}{x}{)}}$$与$${{g}{(}{x}{)}}$$图象的是()
D
A.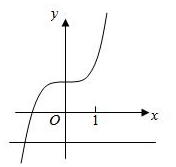
B.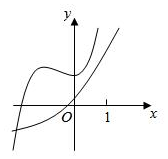
C.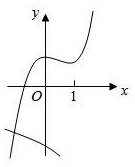
D.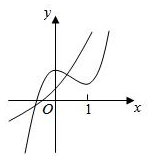
正确率40.0%由于盐碱化严重,某地的耕地面积在最近$${{5}{0}}$$年内减少了$${{1}{0}{%}}$$.如果按此规律,设$${{2}{0}{1}{3}}$$年的耕地面积为$${{m}}$$,则$${{2}{0}{1}{8}}$$年的耕地面积为()
B
A.$$y=( 1-0. 1^{2 5 0} ) m$$
B.$$y=0. 9^{\frac{1} {1 0}} \, m$$
C.$$y=0. 9^{2 5 0} m$$
D.$$y=\left( 1-0. 9^{\frac{1} {1 0}} \right) m$$
1. 解析: 指数函数的标准形式为 $$y = a^x$$($$a > 0$$ 且 $$a \neq 1$$)。
① $$y = \left( \frac{1}{2} \right)^{x-1}$$ 可以变形为 $$y = 2 \cdot \left( \frac{1}{2} \right)^x$$,不符合标准形式。
② $$y = m^x$$ 满足 $$m > 0$$ 且 $$m \neq 1$$,是指数函数。
③ $$y = 1^x$$ 中底数为 1,不符合 $$a \neq 1$$ 的条件。
④ $$y = \left( \frac{1}{2} \right)^{2x} - 1$$ 不是标准指数函数。
综上,只有②是指数函数,答案为 B。
2. 解析: 将各点代入函数 $$f(x) = 2^x - 1$$ 验证:
A. $$f(0) = 2^0 - 1 = 0$$,点在图像上。
B. $$f(0) = 0 \neq 1$$,不在图像上。
C. $$f(1) = 2^1 - 1 = 1 \neq 0$$,不在图像上。
D. $$f(1) = 1 \neq 2$$,不在图像上。
答案为 A。
3. 解析: 指数函数 $$y = (a+2)^x$$ 需满足 $$a+2 > 0$$ 且 $$a+2 \neq 1$$,即 $$a > -2$$ 且 $$a \neq -1$$。
答案为 C。
4. 解析: 设指数函数为 $$f(x) = a^x$$,代入点 $$(3, 8)$$ 得 $$a^3 = 8$$,解得 $$a = 2$$。
故解析式为 $$f(x) = 2^x$$,答案为 B。
5. 解析: 函数 $$g(x)$$ 有两个零点,需分段讨论:
1. 当 $$x \leq 0$$ 时,$$g(x) = e^x + x + a$$,要求 $$e^x + x + a = 0$$ 有解。
2. 当 $$x > 0$$ 时,$$g(x) = \ln x + x + a$$,要求 $$\ln x + x + a = 0$$ 有解。
分析可得 $$a \in [-1, +\infty)$$,答案为 C。
6. 解析: 函数 $$y = (2a^2 - 3a + 2)a^x$$ 是指数函数,需满足 $$2a^2 - 3a + 2 = 1$$ 且 $$a > 0$$、$$a \neq 1$$。
解方程得 $$a = \frac{1}{2}$$,答案为 C。
7. 解析: 代入点 $$P(3, 27)$$ 得 $$a^3 = 27$$,解得 $$a = 3$$。
故 $$f(2) = 3^2 = 9$$,答案为 D。
8. 解析: 代入点 $$(3, 27)$$ 得 $$a^3 = 27$$,解得 $$a = 3$$,答案为 A。
9. 解析: 分析函数 $$f(x) = a \cdot 2^x - 1$$ 和 $$g(x) = x^3 + a x^2 + 1$$ 的图像:
- 当 $$a > 0$$ 时,$$f(x)$$ 单调递增,$$g(x)$$ 可能有极值点。
- 当 $$a < 0$$ 时,$$f(x)$$ 单调递减,$$g(x)$$ 可能有极值点。
通过图像分析,选项 D 不可能成立。
10. 解析: 耕地面积每年减少的比例为 $$0.9^{1/50}$$,5 年后的面积为 $$m \cdot 0.9^{5/50} = m \cdot 0.9^{1/10}$$。
答案为 B。
.jpg)