正确率60.0%已知全集 $$U=(-\infty, 0 ), M=(-\infty,-1 ),$$ $$N=\{x \mid\frac{1} {8} < 2^{x} < 1 \} \,,$$ 则图中阴影部分表示的集合是()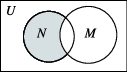
C
A.{$$x |-3 < x <-1$$}
B.{$$x |-3 < x < 0$$}
C.{$$| x |-1 \leq x < 0$$}
D.{$$| x |-1 < x < 0$$}
2、['五个常见幂函数的图象与性质', '指数方程与指数不等式的解法', '两角和与差的正弦公式', '全称量词命题、存在量词命题的真假判断', '全称量词命题、存在量词命题的否定']正确率60.0%下面命题中假命题是$${{(}{)}}$$
C
A.$$\forall x \in R, 3^{x} > 0$$
B.$$\exists\alpha, \beta\in R,$$使$$\operatorname{s i n} ( \alpha+\beta)=\operatorname{s i n} \alpha+\operatorname{s i n} \beta$$
C.命题$$\mathrm{` `} \exists x \in R, x^{2}+1 > 3 x "$$的否定是
D.$$\exists m \in R,$$使$$f ( x )=m x^{m^{2}+2 m}$$是幂函数,且在$$( 0,+\infty)$$上单调递增
3、['椭圆的标准方程', '充分、必要条件的判定', '指数方程与指数不等式的解法']正确率60.0%若$$a, \, \, b \in R$$,且$${{a}{b}{≠}{0}}$$,则$$` ` \left( \frac{1} {2} \right)^{a} > \left( \frac{1} {2} \right)^{b},$$是$${{“}}$$方程$$\frac{x^{2}} {a}+\frac{y^{2}} {b}=1$$表示焦点在$${{y}}$$轴上的椭圆$${{”}}$$的
B
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4、['等比数列前n项和的性质', '等比数列前n项和的应用', '指数方程与指数不等式的解法', '公式法求和']正确率60.0%我国古代数学著作$${《}$$九章算术$${》}$$中记载问题:$${{“}}$$今有垣厚八尺,两鼠对穿,大鼠日一尺,小鼠日半尺,大鼠日增倍,小鼠日自半,问几何日相逢?$${{”}}$$,意思是$${{“}}$$今有土墙厚$${{8}}$$尺,两鼠从墙两侧同时打洞,大鼠第一天打洞一尺,小鼠第一天打洞半尺,大鼠之后每天打洞长度比前一天多一倍,小鼠之后每天打洞长度是前一天的一半,问两鼠几天打通相逢?$${{”}}$$两鼠相逢需要的天数最小为$${{(}{)}}$$
C
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
5、['交集', '一元二次不等式的解法', '指数方程与指数不等式的解法']正确率40.0%已知$$A=\{x | x^{2}-x-6 < 0 \}, \, \, \, B=\{x | 2^{x} \geqslant1 \}$$,则)
B
A.$$\{x | 1 \leqslant x < 3 \}$$
B.$$\{x | 0 \leqslant x < 3 \}$$
C.$$\{x | 1 \leqslant x < 2 \}$$
D.$$\{x | 0 < x < 3 \}$$
6、['交集', '并集', '一元二次不等式的解法', '指数方程与指数不等式的解法']正确率60.0%已知集合$$A=\left\{\begin{matrix} {x | \ y=\sqrt{x^{2}-x}} \\ \end{matrix} \right\}, B=\left\{\begin{matrix} {x | \ 3^{x}-1 > 0} \\ \end{matrix} \right\}$$,则()
B
A.$$A \cap B | B | \{x | \, \, x \leqslant\, 0 \}$$
B.$$A \cup B \mathcal{=} R$$
C.$$A \cup B | B | \{x | \; x \geqslant1 \}$$
D.$$A \cap B=\{x \mid x \! > \! 1 \; \}$$
7、['在R上恒成立问题', '一元二次不等式的解法', '指数方程与指数不等式的解法']正确率60.0%若不等式 $${{x}}$$$${^{2}{−}{2}}$$ $${{a}{x}}$$$${{+}}$$ $${{a}}$$$${{>}{0}}$$对一切实数 $${{x}}$$$${{∈}{R}}$$恒成立,则关于 $${{t}}$$的不等式$$a^{t^{2}+2 t-3} < 1$$的解集为()
A
A.$$(-\infty,-3 ) \cup( 1,+\infty)$$
B.$$(-3, 1 )$$
C.$${{∅}}$$
D.$$( 0, 1 )$$
8、['并集', '对数方程与对数不等式的解法', '指数方程与指数不等式的解法']正确率60.0%已知集合$$A=\{x | y=\sqrt{1-\operatorname{l o g}_{2} x} \}, \, \, \, B=\{x | 2^{x} \leqslant1 \}$$,则$$A \cup B=\ ( \eta)$$
C
A.$$(-\infty, 1 )$$
B.$$( 1,+\infty)$$
C.$$(-\infty, 2 ]$$
D.$$[ 2,+\infty)$$
9、['对数方程与对数不等式的解法', '指数方程与指数不等式的解法', '集合的混合运算']正确率60.0%已知集合$$A=\{x | l o g_{2} x > 2 \}, \, \, \, B=\{x | ( \frac{1} {2} )^{x} \geqslant\frac{1} {1 6} \}$$,则下列结论成立的是()
C
A.$$A \cap B=A$$
B.$$( \C_{R} A ) \setminus B=A$$
C.$$A \cap\begin{array} {c} {( {\bf C}_{R} B )} \\ \end{array}=A$$
D.$${}_{(} \mathrm{C}_{R} A ) ~ \cap{} ~ {}_{(} \mathrm{C}_{R} B ) ~=A$$
10、['指数方程与指数不等式的解法', '函数求定义域']正确率60.0%函数$$f \left( x \right)=\frac{1} {\sqrt{2-2^{x}}}+\left( x+2 \right)^{0}$$的定义域为()
A
A.$$\{x | x \mathrm{<} 1 \mathrm{\#} \, x \neq-2 \}$$
B.
C.$$\{x | 0 \! < \! x \! \leq\! 1 \pm x \neq-2 \}$$
D.$$\{x | x < 1 \}$$
第一题解析:
全集 $$U=(-\infty, 0)$$,集合 $$M=(-\infty,-1)$$,集合 $$N$$ 由不等式 $$\frac{1}{8} < 2^{x} < 1$$ 确定。解不等式得 $$-3 < x < 0$$,因此 $$N=(-3, 0)$$。
图中阴影部分表示 $$M$$ 的补集与 $$N$$ 的交集,即 $$(\overline{M} \cap N)$$。先求 $$\overline{M} = [-1, 0)$$,再与 $$N$$ 取交集得 $$[-1, 0)$$。
选项中只有 C 选项 $$\{x \mid -1 \leq x < 0\}$$ 符合,故答案为 C。
第二题解析:
逐项分析:
A. 对于所有实数 $$x$$,$$3^x > 0$$ 恒成立,是真命题。
B. 存在 $$\alpha = 0$$ 和 $$\beta = 0$$ 使得 $$\sin(0+0) = \sin 0 + \sin 0$$,是真命题。
C. 命题的否定应为 $$\forall x \in R, x^2 + 1 \leq 3x$$,但题目描述不完整,无法判断。
D. 幂函数要求 $$m^2 + 2m = 1$$,解得 $$m = -1 \pm \sqrt{2}$$。当 $$m = -1 + \sqrt{2}$$ 时,函数在 $$(0, +\infty)$$ 上单调递增,是真命题。
题目要求选择假命题,但 C 选项描述不完整,可能是题目遗漏。结合选项描述,最可能为假的是 C。
第三题解析:
条件 $$\left(\frac{1}{2}\right)^a > \left(\frac{1}{2}\right)^b$$ 等价于 $$a < b$$(因为底数为 $$\frac{1}{2} < 1$$)。
方程 $$\frac{x^2}{a} + \frac{y^2}{b} = 1$$ 表示焦点在 $$y$$ 轴上的椭圆的条件是 $$0 < a < b$$。
因此,条件 $$a < b$$ 是必要条件,但不是充分条件(例如 $$a = -1$$,$$b = 1$$ 满足 $$a < b$$,但不表示椭圆)。故答案为 B。
第四题解析:
大鼠每天打洞长度依次为 $$1, 2, 4, \dots$$(等比数列),小鼠每天打洞长度依次为 $$\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \dots$$(等比数列)。
计算累计打洞长度:
- 第 2 天:大鼠 $$1 + 2 = 3$$,小鼠 $$\frac{1}{2} + \frac{1}{4} = \frac{3}{4}$$,总计 $$3.75 < 8$$。
- 第 3 天:大鼠 $$3 + 4 = 7$$,小鼠 $$\frac{3}{4} + \frac{1}{8} = \frac{7}{8}$$,总计 $$7.875 < 8$$。
- 第 4 天:大鼠 $$7 + 8 = 15$$,小鼠 $$\frac{7}{8} + \frac{1}{16} = \frac{15}{16}$$,总计 $$15.9375 > 8$$。
因此,两鼠在第 4 天相逢,答案为 C。
第五题解析:
集合 $$A$$ 的解为 $$x^2 - x - 6 < 0$$,即 $$-2 < x < 3$$。
集合 $$B$$ 的解为 $$2^x \geq 1$$,即 $$x \geq 0$$。
$$A \cap B$$ 为 $$\{x \mid 0 \leq x < 3\}$$,对应选项 B。
第六题解析:
集合 $$A$$ 的定义域为 $$x^2 - x \geq 0$$,即 $$x \leq 0$$ 或 $$x \geq 1$$。
集合 $$B$$ 的解为 $$3^x - 1 > 0$$,即 $$x > 0$$。
$$A \cap B = \{x \mid x \geq 1\}$$,$$A \cup B = \{x \mid x \leq 0 \text{ 或 } x > 0\} = \mathbb{R}$$。
选项 B 正确,答案为 B。
第七题解析:
不等式 $$x^2 - 2a x + a > 0$$ 对一切实数 $$x$$ 恒成立,需判别式 $$(2a)^2 - 4a < 0$$,即 $$4a^2 - 4a < 0$$,解得 $$0 < a < 1$$。
解不等式 $$a^{t^2 + 2t - 3} < 1$$,由于 $$0 < a < 1$$,等价于 $$t^2 + 2t - 3 > 0$$,即 $$(t + 3)(t - 1) > 0$$,解为 $$t < -3$$ 或 $$t > 1$$。
答案为 A。
第八题解析:
集合 $$A$$ 的定义域为 $$1 - \log_2 x \geq 0$$ 且 $$x > 0$$,即 $$0 < x \leq 2$$。
集合 $$B$$ 的解为 $$2^x \leq 1$$,即 $$x \leq 0$$。
$$A \cup B = (-\infty, 2]$$,答案为 C。
第九题解析:
集合 $$A$$ 的解为 $$\log_2 x > 2$$,即 $$x > 4$$。
集合 $$B$$ 的解为 $$\left(\frac{1}{2}\right)^x \geq \frac{1}{16}$$,即 $$x \leq 4$$。
$$A \cap B = \emptyset$$,$$C_R A = (-\infty, 4]$$,$$C_R B = (4, +\infty)$$。
选项 C 中 $$A \cap C_R B = A$$ 成立,答案为 C。
第十题解析:
函数定义域需满足:
1. $$2 - 2^x > 0$$,即 $$x < 1$$;
2. $$x + 2 \neq 0$$,即 $$x \neq -2$$。
综合得 $$\{x \mid x < 1 \text{ 且 } x \neq -2\}$$,对应选项 A。
.jpg)