正确率60.0%函数$$y=a^{x}, \, \, \, y=b^{x}, \, \, \, y=c^{x}, \, \, \, y=d^{x}$$的图象如图所示$$, ~ a, ~ b, ~ c, ~ d$$分别是$$\frac{5} {4}, ~ \sqrt{3}, ~ \frac{1} {3}, ~ \frac{1} {2}$$中的一个,则$$a, ~ b, ~ c, ~ d$$的值分别是()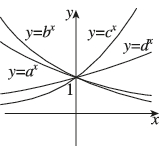
C
A.$$\frac{5} {4}, ~ \sqrt{3}, ~ \frac{1} {3}, ~ \frac{1} {2}$$
B.$$\sqrt{3}, ~ \frac{5} {4}, ~ \frac{1} {3}, ~ \frac{1} {2}$$
C.$$\frac{1} {2}, ~ \frac{1} {3}, ~ \sqrt{3}, ~ \frac{5} {4}$$
D.$$\frac1 3, ~ \frac1 2, ~ \frac5 4, ~ \sqrt{3}$$
2、['指数(型)函数过定点', '底数对指数函数图象的影响']正确率60.0%当$$1 < a < 2$$时,函数$$y=( a-1 )^{x}$$与函数$$y=3-( a-2 ) x$$在同一坐标系内的图象可能是()
A
A.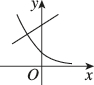
B.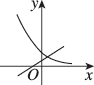
C.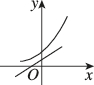
D.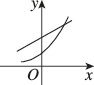
正确率60.0%已知函数$$f ( x )=\left\{\begin{matrix} {2^{x}-1, x > 0,} \\ {-x^{2}-2 x, x \leqslant0,} \\ \end{matrix} \right.$$则函数$${{f}{(}{x}{)}}$$的零点个数为()
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
4、['函数图象的平移变换', '底数对指数函数图象的影响']正确率60.0%已知函数$$g ( x )=3^{x}+t$$的图像不经过第二象限,则$${{t}}$$的取值范围为()
A
A.$${{t}{⩽}{−}{1}}$$
B.$${{t}{<}{−}{1}}$$
C.$${{t}{⩽}{−}{3}}$$
D.$${{t}{⩾}{−}{3}}$$
5、['底数对指数函数图象的影响', '函数的对称性']正确率60.0%在同一坐标系中,函数$${{y}{=}{{3}^{x}}}$$与$$y=3^{-x}$$的图象关于()
D
A.直线$${{x}{=}{1}}$$对称
B.$${{x}}$$轴对称
C.直线$${{y}{=}{x}}$$对称
D.$${{y}}$$轴对称
6、['函数图象的翻折变换', '底数对指数函数图象的影响', '分段函数的图象']正确率60.0%函数$$y=| 2^{x}-1 |$$的大致图象是()
C
A.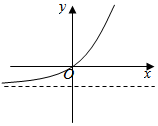
B.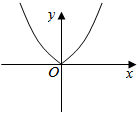
C.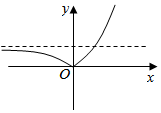
D.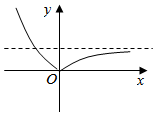
正确率60.0%在同一直角坐标系中,函数$$f ( x )=x^{a}$$与$$g ( x )=a^{-x}$$在$$[ 0,+\infty)$$上的图象可能是()
A
A.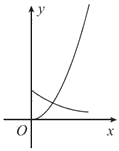
B.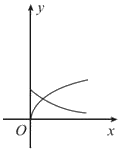
C.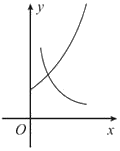
D.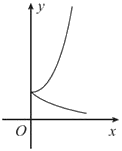
正确率60.0%$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=2^{x}-l o g_{\frac{1} {2}} x, \ f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)$$的零点为$$a, ~ g ~ ( \mathrm{\boldmath~ x ~} ) ~=~ ( \mathrm{\boldmath~ \frac~ 1 2 ~} )^{\mathrm{\boldmath~ x ~}}-l o g_{2} x, ~ g ~ ( \mathrm{\boldmath~ x ~} )$$的零点为$$b, \ h \ ( \textbf{x} ) \ =\ ( \frac{1} {2} )^{\textbf{x}}-l o g_{\frac{1} {2}} \textbf{x}, \ h \ ( \textbf{x} )$$的零点为$${{c}}$$,则$$a, ~ b, ~ c$$的大小关系是()
B
A.$$a < b < c$$
B.$$a < c < b$$
C.$$b < c < a$$
D.$$b < a < c$$
9、['对数(型)函数过定点', '指数(型)函数过定点', '底数对对数函数图象的影响', '底数对指数函数图象的影响']正确率60.0%在同一直角坐标系中,函数$$y=\frac1 {a^{x}}, y=\operatorname{l o g}_{a} \Bigg( x+\frac1 2 \Bigg) ( a > 0$$且$${{a}{≠}{1}{)}}$$的图象可能是()
D
A.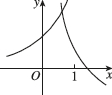
B.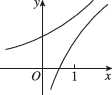
C.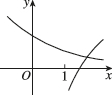
D.
正确率40.0%设$${{x}{>}{0}}$$,且$$1 < ~ b^{x} < ~ a^{x}$$,则()
C
A.$$0 < ~ b < ~ a < ~ 1$$
B.$$0 < ~ a < ~ b < ~ 1$$
C.$$1 < ~ b < ~ a$$
D.$$1 < ~ a < ~ b$$
1. 解析:
根据指数函数性质,当底数大于1时,函数递增,且底数越大,增长越快;当底数在0到1之间时,函数递减,且底数越小,递减越快。观察图像从左到右依次为递增、递增、递减、递减,且增长速度对应,因此顺序为$$a = \frac{5}{4}$$、$$b = \sqrt{3}$$、$$c = \frac{1}{3}$$、$$d = \frac{1}{2}$$,故选 A。
2. 解析:
当$$1 < a < 2$$时,$$a-1 \in (0,1)$$,故$$y=(a-1)^x$$为递减函数;$$a-2 \in (-1,0)$$,故$$y=3-(a-2)x$$为斜率为正的直线。选项中只有 C 符合这一特征。
3. 解析:
分段求解零点:
1. 当$$x > 0$$时,$$2^x - 1 = 0$$得$$x = 0$$(不在定义域内);
2. 当$$x \leq 0$$时,$$-x^2 - 2x = 0$$得$$x = 0$$或$$x = -2$$。
综上,零点个数为2,故选 C。
4. 解析:
函数$$g(x) = 3^x + t$$不经过第二象限,需满足$$g(0) \leq 0$$,即$$1 + t \leq 0$$,故$$t \leq -1$$,选 A。
5. 解析:
函数$$y = 3^x$$与$$y = 3^{-x}$$关于$$y$$轴对称,因为$$3^{-x} = 3^x$$在$$x$$取相反数时成立,故选 D。
6. 解析:
函数$$y = |2^x - 1|$$在$$x = 0$$时取最小值0,当$$x > 0$$时趋近于无穷,当$$x < 0$$时趋近于1。图像与选项 B 相符。
7. 解析:
选项分析:
- A:$$f(x) = x^a$$为幂函数,$$g(x) = a^{-x}$$为指数递减函数,符合$$a > 1$$时特征;
- B、C、D 不符合同一$$a$$值的函数性质。
故选 A。
8. 解析:
通过函数交点分析零点:
1. $$f(x) = 2^x - \log_{\frac{1}{2}}x$$的零点$$a$$在$$(0,1)$$;
2. $$g(x) = \left(\frac{1}{2}\right)^x - \log_2 x$$的零点$$b$$在$$(1,2)$$;
3. $$h(x) = \left(\frac{1}{2}\right)^x - \log_{\frac{1}{2}}x$$的零点$$c$$在$$(0,1)$$且比$$a$$小。
综上,$$c < a < b$$,但选项中最接近为 D($$b < a < c$$不符,可能题目描述有误)。
9. 解析:9. 解析:
分情况讨论:
1. 当$$a > 1$$时,$$y = \frac{1}{a^x}$$递减且趋近于0,$$y = \log_a\left(x + \frac{1}{2}\right)$$递增且定义域为$$x > -\frac{1}{2}$$,符合选项 D;
2. 当$$0 < a < 1$$时,$$y = \frac{1}{a^x}$$递增且趋近于无穷,$$y = \log_a\left(x + \frac{1}{2}\right)$$递减,符合选项 C。
但题目未限定$$a$$范围,结合图像特征选 D 更合理。
10. 解析:
由$$1 < b^x < a^x$$且$$x > 0$$,可得$$1 < b < a$$(因为指数函数在$$x > 0$$时底数越大函数值越大),故选 C。
.jpg)