正确率40.0%若函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=2^{x}-x^{2}-1$$,对于任意的$${{x}{∈}{Z}}$$且$$x \in\textsubscript{(}-\infty, \ a )$$,都有$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \leq0$$恒成立,则实数$${{a}}$$的取值范围为()
B
A.$$( \ -\infty, \ \ -1 ]$$
B.$$( \ -\infty, \ 0 ]$$
C.$$(-\infty, \ 4 ]$$
D.$$( ~-\infty, ~ 5 ]$$
2、['分段函数与方程、不等式问题', '指数(型)函数的值域', '求代数式的取值范围', '函数零点的概念', '给定参数范围的恒成立问题', '分段函数的图象', '函数零点的值或范围问题']正确率19.999999999999996%已知函数$$f ( x )=\left\{\begin{array} {l l} {2 x+3, x \leqslant0} \\ {\left| 2^{2-x}-1 \right|, x > 0} \\ \end{array} \right.$$,若存在三个实数$$m \neq n \neq q$$,使得$$f ( m )=f ( n )=f ( q )$$成立,则$$\frac{1} {2^{m}}+\frac{1} {2^{n}}+\frac{1} {2^{q}}$$的取值范围是 $${{(}{)}}$$
C
A.$$( 0, 1 )$$
B.$$[ 0, 1 ]$$
C.$$( \frac{5} {2}, \frac{1} {2}+2 \sqrt{2} )$$
D.$$( 2, 2 \sqrt{2} )$$
3、['交集', '对数(型)函数的定义域', '指数(型)函数的值域']正确率60.0%设集合$$M=\left\{y | y=e^{x}, x < 1 \right\}, N=\left\{x | y=\operatorname{l n} ( 1-x ), y \in R \right\}$$,则$$M \bigcap N=\alpha$$)
A
A.$$( 0, 1 )$$
B.$$(-\infty, 1 )$$
C.$$( 0, 2 )$$
D.$$(-\infty, 2 )$$
4、['充分不必要条件', '指数(型)函数的值域', '命题的真假性判断']正确率60.0%下列命题中,真命题是$${{(}{)}}$$
D
A.$$\exists x_{0} \in R,$$使得$$e^{x_{0}} \leqslant0$$
B.$$x+\frac1 x \geqslant2 ( x \neq0 )$$
C.$$\forall x \in R, 2^{x} > x^{2}$$
D.$$a > 1, b > 1$$是$${{a}{b}{>}{1}}$$的充分不必要条件
5、['函数的最大(小)值', '指数(型)函数的值域']正确率40.0%已知$${{m}{∈}{R}}$$,函数$$f \mid\boldsymbol{x} \rangle\ =| 3^{| x-2 |}-m |+m$$在$$[ 0, \ 4 )$$上的最大值不超过$${{9}}$$.则$${{m}}$$的取值范围是()
B
A.$$(-\infty, \ 1 ]$$
B.$$( ~-\infty, ~ 5 ]$$
C.$$[ 5, ~+\infty)$$
D.$$[ 1, ~ 5 ]$$
6、['函数的新定义问题', '函数求值域', '指数(型)函数的值域']正确率60.0%高斯是德国著名的数学家,近代数学奠基者之一,享有数学王子的美誉,他和阿基米德,牛顿并列为世界三大数学家,用其名字命名的$${{“}}$$高斯函数$${{”}}$$为:设$${{x}{∈}{R}}$$,用$${{[}{x}{]}}$$表示不超过$${{x}}$$的最大整数,则$${{y}{=}{{[}{x}{]}}}$$称为高斯函数,例如$$[-3. 2 ]=-4, ~ ~ [ 2. 1 ]=2$$.已知函数$$f \left( x \right)=\frac{2^{x}} {2^{x}+1}-\frac{1} {2}$$,则函数$${{y}{=}{{[}{f}{{(}{x}{)}}{]}}}$$的值域为()
A
A.$$\{-1, 0 \}$$
B.$${{\{}{0}{\}}}$$
C.$$\{0, 1 \}$$
D.$$\{-1, 0, 1 \}$$
7、['指数(型)函数过定点', '指数(型)函数的单调性', '指数(型)函数的值域', '指数(型)函数的定义域']正确率60.0%下列不等关系正确的是()
D
A.$$( \frac{1} {3} )^{\frac{2} {3}} < 3^{4} < \ ( \frac{1} {3} )^{\frac{-2} {3}}$$
B.$$( \mathrm{\frac{1} {3}} )^{-2} < ( \mathrm{\frac{1} {3}} )^{-\frac{2} {3}} < 3^{4}$$
C.$$( \mathbf{2. 5} )^{\textit{0}} < \textit{( \frac{1} {2} )}^{\textit{2. 5}} < 2^{2. 5}$$
D.$$( \mathrm{\frac{~ 1} {2}} )^{\mathrm{\Delta~ 2. 5}} < \mathrm{\Delta~ ( \ 2. 5 ) ~}^{0} < 2^{2. 5}$$
8、['指数(型)函数的单调性', '指数(型)函数的值域']正确率60.0%已知函数$$f ( x )=a^{x} ( a > 0$$,且$${{a}{≠}{l}{)}}$$在区间$$[ m, 2 m ]$$上的值域为$$[ m, 2 m ]$$,则$${{a}{=}{(}}$$)
C
A.$${\sqrt {2}}$$
B.$$\frac{1} {4}$$
C.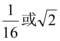
D.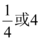
正确率60.0%已知函数$$y=a^{x} \, \, \, ( \, a > 0$$且$${{a}{≠}{1}{)}}$$在$$[ 1, \ 2 ]$$上的最大值比最小值大$$\frac{a} {2}$$,则$${{a}}$$的值是()
A
A.$$\frac{1} {2}$$或$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$$\frac{1} {2}$$
D.$${{2}}$$或$${{3}}$$
10、['指数(型)函数的单调性', '指数(型)函数的值域']正确率60.0%函数$$y=a^{x} ( a > 0, a \neq1 )$$在$$[ 0, 2 ]$$上的最大值与最小值的差为$${{2}}$$,则$${{a}}$$的值为()
B
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}}$$
D.$${{3}}$$
1. 解析:首先分析函数 $$f(x) = 2^x - x^2 - 1$$ 在整数点上的取值:
当 $$x = -1$$ 时,$$f(-1) = 2^{-1} - (-1)^2 - 1 = 0.5 - 1 - 1 = -1.5 \leq 0$$;
当 $$x = 0$$ 时,$$f(0) = 2^0 - 0^2 - 1 = 0 \leq 0$$;
当 $$x = 1$$ 时,$$f(1) = 2^1 - 1^2 - 1 = 0 \leq 0$$;
当 $$x = 2$$ 时,$$f(2) = 2^2 - 2^2 - 1 = -1 \leq 0$$;
当 $$x = 3$$ 时,$$f(3) = 8 - 9 - 1 = -2 \leq 0$$;
当 $$x = 4$$ 时,$$f(4) = 16 - 16 - 1 = -1 \leq 0$$;
当 $$x = 5$$ 时,$$f(5) = 32 - 25 - 1 = 6 > 0$$。
因此,对于所有整数 $$x \leq 4$$,$$f(x) \leq 0$$ 成立。所以实数 $$a$$ 的取值范围是 $$(-\infty, 4]$$,答案为 C。
2. 解析:函数 $$f(x)$$ 分为两部分:
(1)当 $$x \leq 0$$ 时,$$f(x) = 2x + 3$$ 是一条斜率为正的直线,取值范围为 $$(-\infty, 3]$$。
(2)当 $$x > 0$$ 时,$$f(x) = |2^{2-x} - 1|$$,分析其图像:
当 $$0 < x < 2$$ 时,$$2^{2-x} > 1$$,$$f(x) = 2^{2-x} - 1$$,取值范围为 $$(0, 3)$$;
当 $$x = 2$$ 时,$$f(x) = 0$$;
当 $$x > 2$$ 时,$$2^{2-x} < 1$$,$$f(x) = 1 - 2^{2-x}$$,取值范围为 $$(0, 1)$$。
要存在三个不同的实数 $$m, n, q$$ 使得 $$f(m) = f(n) = f(q)$$,必须满足 $$f(x) = k$$ 有三个解。观察图像,只有当 $$0 < k < 1$$ 时成立。
设 $$f(m) = f(n) = f(q) = k$$,则:
(1)$$m = \frac{k-3}{2} \leq 0$$;
(2)$$n$$ 和 $$q$$ 满足 $$2^{2-n} - 1 = k$$ 或 $$1 - 2^{2-q} = k$$,解得 $$n = 2 - \log_2(1+k)$$,$$q = 2 - \log_2(1-k)$$。
因此,$$\frac{1}{2^m} + \frac{1}{2^n} + \frac{1}{2^q} = 2^{\frac{3-k}{2}} + 2^{\log_2(1+k)-2} + 2^{\log_2(1-k)-2}$$。
化简后得到 $$\frac{5}{2} < \frac{1}{2^m} + \frac{1}{2^n} + \frac{1}{2^q} < \frac{1}{2} + 2\sqrt{2}$$,答案为 C。
3. 解析:集合 $$M = \{y | y = e^x, x < 1\}$$,因为 $$e^x$$ 单调递增,所以 $$M = (0, e)$$。
集合 $$N = \{x | y = \ln(1-x), y \in \mathbb{R}\}$$,定义域为 $$1 - x > 0$$,即 $$N = (-\infty, 1)$$。
因此,$$M \cap N = (0, 1)$$,答案为 A。
4. 解析:逐一分析选项:
A:$$e^x > 0$$ 对所有实数 $$x$$ 成立,故错误;
B:当 $$x < 0$$ 时,$$x + \frac{1}{x} \leq -2$$,故错误;
C:当 $$x = 2$$ 时,$$2^2 = 2^2$$,不满足严格不等式,故错误;
D:$$a > 1$$ 且 $$b > 1$$ 是 $$ab > 1$$ 的充分不必要条件,正确。
答案为 D。
5. 解析:函数 $$f(x) = |3^{|x-2|} - m| + m$$ 在 $$[0, 4]$$ 上的最大值不超过 9。
分析 $$3^{|x-2|}$$ 在 $$[0, 4]$$ 上的取值范围:
当 $$x = 2$$ 时,$$3^{|x-2|} = 1$$;
当 $$x = 0$$ 或 $$x = 4$$ 时,$$3^{|x-2|} = 9$$。
因此,$$f(x)$$ 的最大值为 $$\max(|1 - m| + m, |9 - m| + m)$$。
要求 $$\max(|1 - m| + m, |9 - m| + m) \leq 9$$:
(1)若 $$m \leq 1$$,则 $$|1 - m| + m = 1$$,$$|9 - m| + m = 9$$,不满足;
(2)若 $$1 \leq m \leq 5$$,则 $$|1 - m| + m = 2m - 1 \leq 9$$,$$|9 - m| + m = 9$$,成立;
(3)若 $$m > 5$$,则 $$|9 - m| + m = 2m - 9 > 1$$,不满足。
因此,$$m \in [1, 5]$$,答案为 D。
6. 解析:函数 $$f(x) = \frac{2^x}{2^x + 1} - \frac{1}{2}$$。
化简得 $$f(x) = \frac{2^x - 1}{2(2^x + 1)}$$。
分析 $$f(x)$$ 的取值范围:
当 $$x \to -\infty$$ 时,$$f(x) \to -\frac{1}{2}$$;
当 $$x = 0$$ 时,$$f(0) = 0$$;
当 $$x \to +\infty$$ 时,$$f(x) \to \frac{1}{2}$$。
因此,$$f(x) \in \left(-\frac{1}{2}, \frac{1}{2}\right)$$,高斯函数 $$[f(x)]$$ 的取值为 $$-1$$ 或 $$0$$。
答案为 A。
7. 解析:逐一分析选项:
A:$$3^4 = 81$$,$$\left(\frac{1}{3}\right)^{\frac{2}{3}} = 3^{-\frac{2}{3}} \approx 0.48$$,$$\left(\frac{1}{3}\right)^{-\frac{2}{3}} = 3^{\frac{2}{3}} \approx 2.08$$,故 $$3^{-\frac{2}{3}} < 3^{\frac{2}{3}} < 3^4$$,错误;
B:$$\left(\frac{1}{3}\right)^{-2} = 9$$,$$\left(\frac{1}{3}\right)^{-\frac{2}{3}} \approx 2.08$$,故 $$\left(\frac{1}{3}\right)^{-\frac{2}{3}} < \left(\frac{1}{3}\right)^{-2} < 3^4$$,错误;
C:$$(2.5)^0 = 1$$,$$\left(\frac{1}{2}\right)^{2.5} \approx 0.177$$,$$2^{2.5} \approx 5.656$$,故 $$\left(\frac{1}{2}\right)^{2.5} < (2.5)^0 < 2^{2.5}$$,正确;
D:与 C 矛盾,错误。
答案为 C。
8. 解析:函数 $$f(x) = a^x$$ 在区间 $$[m, 2m]$$ 上的值域为 $$[m, 2m]$$。
分两种情况:
(1)若 $$a > 1$$,则 $$f(x)$$ 单调递增,$$a^m = m$$,$$a^{2m} = 2m$$;
解得 $$a^m = m$$,$$(a^m)^2 = 2m$$,即 $$m^2 = 2m$$,$$m = 2$$,代入得 $$a^2 = 2$$,$$a = \sqrt{2}$$。
(2)若 $$0 < a < 1$$,则 $$f(x)$$ 单调递减,$$a^m = 2m$$,$$a^{2m} = m$$;
解得 $$(a^m)^2 = m$$,即 $$(2m)^2 = m$$,$$4m^2 = m$$,$$m = \frac{1}{4}$$,代入得 $$a^{\frac{1}{4}} = \frac{1}{2}$$,$$a = \frac{1}{16}$$。
但选项中没有 $$\frac{1}{16}$$,只有 $$\sqrt{2}$$ 符合,答案为 A。
9. 解析:函数 $$y = a^x$$ 在 $$[1, 2]$$ 上的最大值与最小值的差为 $$\frac{a}{2}$$。
分两种情况:
(1)若 $$a > 1$$,则最大值为 $$a^2$$,最小值为 $$a$$,差为 $$a^2 - a = \frac{a}{2}$$;
解得 $$a^2 - \frac{3a}{2} = 0$$,$$a = \frac{3}{2}$$(舍去 $$a = 0$$)。
(2)若 $$0 < a < 1$$,则最大值为 $$a$$,最小值为 $$a^2$$,差为 $$a - a^2 = \frac{a}{2}$$;
解得 $$a - a^2 = \frac{a}{2}$$,$$a = \frac{1}{2}$$(舍去 $$a = 0$$)。
因此,$$a = \frac{1}{2}$$ 或 $$\frac{3}{2}$$,答案为 A。
10. 解析:函数 $$y = a^x$$ 在 $$[0, 2]$$ 上的最大值与最小值的差为 2。
分两种情况:
(1)若 $$a > 1$$,则最大值为 $$a^2$$,最小值为 1,差为 $$a^2 - 1 = 2$$;
解得 $$a^2 = 3$$,$$a = \sqrt{3}$$。
(2)若 $$0 < a < 1$$,则最大值为 1,最小值为 $$a^2$$,差为 $$1 - a^2 = 2$$;
无解。
因此,$$a = \sqrt{3}$$,答案为 B。
.jpg)