正确率80.0%函数$$f ( x )=a^{x-1}+2 ( a > 0$$且$${{a}{≠}{1}{)}}$$的图像过定点()
A
A.$$( 1, ~ 3 )$$
B.$$( 0, \ 3 )$$
C.$$( 1, ~ 2 )$$
D.$$( 0, \ 2 )$$
2、['指数(型)函数过定点', '利用基本不等式求最值']正确率40.0%函数$$y=a^{x-2} \, \left( \begin{matrix} {a > 0} \\ \end{matrix} \right)$$,且$${{a}{≠}{1}{)}}$$的图象恒过定点$${{A}}$$,若点$${{A}}$$在一次函数$$y=m x+4 n$$的图象上,其中$$m, ~ n > 0$$,则$$\frac{1} {m}+\frac{2} {n}$$的最小值为()
C
A.$${{8}}$$
B.$${{9}}$$
C.$${{1}{8}}$$
D.$${{1}{6}}$$
3、['指数函数的定义', '复合函数的单调性判定', '指数(型)函数过定点', '指数(型)函数的单调性', '指数(型)函数的定义域', '指数方程与指数不等式的解法']正确率60.0%使不等式$$2^{3 x-1} > 2$$成立的$${{x}}$$取值范围为()
A
A.$$( \frac{2} {3}, \enspace+\infty)$$
B.$$( 1, ~+\infty)$$
C.$$( \frac{1} {3}, \enskip+\infty)$$
D.$$( \ -\frac{1} {3}, \ \ +\infty)$$
4、['指数(型)函数过定点', '五个常见幂函数的图象与性质', '函数的单调区间']正确率60.0%设函数$$y=a^{x-2}-\frac{1} {2} \mathit{\Lambda} a > 0$$,且$${{a}{≠}{1}{)}}$$的图象恒过定点$${{A}}$$,若点$${{A}}$$在幂函数$${{y}{=}{{x}^{a}}}$$的图象上,则该幂函数的单调递减区间是()
A
A.
B.$$( \mathrm{\bf~ 0}, \mathrm{\bf~ \Lambda}+\infty)$$
C.$$( \mathrm{\mathbf{~-\infty, \ 0 ~}} )$$
D.
正确率60.0%已知函数$$y=a^{x-2}+3 \langle\ a > 0$$且$${{a}{≠}{1}{)}}$$的图象恒过定点$${{P}}$$,点$${{P}}$$在幂函数$$y=f ~ ( x )$$的图象上,则$$f ( \frac{1} {3} )=($$)
A
A.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
B.$${{9}}$$
C.$$\frac{\sqrt{3}} {3}$$
D.$${{3}}$$
6、['指数函数的定义', '抽象函数的应用', '指数(型)函数过定点', '指数(型)函数的单调性', '指数(型)函数的值域', '指数(型)函数的定义域']正确率40.0%定义在$${{R}}$$上的函数$${{f}{(}{x}{)}}$$满足$$f ( 0 )=0, f ( x )+f ( 1-x )=1, f ( \frac{x} {5} )=\frac{1} {2} f ( x )$$,且当$$0 \leqslant x_{1} < x_{2} \leqslant1$$时,$$f ( x_{1} ) \leqslant f ( x_{2} )$$,则$$f ( \frac{1} {2 0 1 8} )$$等于()
B
A.$$\frac{1} {6 4}$$
B.$$\frac{1} {3 2}$$
C.$$\frac{1} {1 6}$$
D.$$\frac{1} {2}$$
7、['指数(型)函数过定点', '指数(型)函数的单调性', '反函数的定义']正确率60.0%已知函数$$f \left( x \right)=\frac{x-1} {a} \, \left( a > 0, \, \, a \neq1 \right)$$,在同一坐标系中,$$y=f^{-1} \left( x \right)$$与$$y=a^{| x-1 |}$$的图象可能是()
C
A.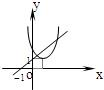
B.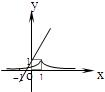
C.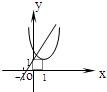
D.
正确率40.0%如果函数$$f \left( x \right)=a^{x}+b-1 \left( a > 0 \ss\alpha a \neq1 \right)$$的图像经过第一$${、}$$二$${、}$$四象限且不经过第三象限,那么一定有$${{(}{)}}$$
B
A.$$0 < a < 1, b > 0$$< a < 1,b >$${{0}}$$
B.$$0 < a < 1, 0 < b < 1$$
C.$$a > 1, b < 0$$
D.$$a > 1, b > 0$$
9、['对数(型)函数过定点', '指数(型)函数过定点']正确率60.0%设$${{a}{>}{0}}$$,且$${{a}{≠}{1}}$$,则函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right)=a^{x}+l o g_{a} \left( \begin{matrix} {x+1} \\ \end{matrix} \right) )+1$$恒过定点()
B
A.$$( {\bf0}, \mathrm{\bf~ 1} )$$
B.$$( {\bf0}, ~ {\bf2} )$$
C.$$( 1, \ 1 )$$
D.$$( 1, \ 2 )$$
10、['指数(型)函数过定点']正确率60.0%函数$$y=a^{x-1}+1 ( 0 < a \neq1 )$$的图象必经过点()
D
A.$$( 0, 1 )$$
B.$$\left( 1, 1 \right)$$
C.$$( 0, 2 )$$
D.$$( 1, 2 )$$
1. 函数 $$f(x) = a^{x-1} + 2$$ 的图像过定点,当指数部分 $$x-1 = 0$$ 时,函数值与 $$a$$ 无关,即 $$x = 1$$。此时 $$f(1) = a^{0} + 2 = 1 + 2 = 3$$,所以定点为 $$(1, 3)$$,选项 A 正确。
2. 函数 $$y = a^{x-2}$$ 的图像恒过定点 $$A$$,当 $$x-2 = 0$$ 时,$$y = 1$$,即 $$A(2, 1)$$。代入直线方程 $$y = mx + 4n$$ 得 $$1 = 2m + 4n$$,即 $$m + 2n = \frac{1}{2}$$。利用不等式 $$\frac{1}{m} + \frac{2}{n} = \left( \frac{1}{m} + \frac{2}{n} \right)(m + 2n) \times 2 \geq 8$$,当且仅当 $$m = n = \frac{1}{4}$$ 时取等,选项 A 正确。
3. 不等式 $$2^{3x-1} > 2$$ 等价于 $$3x - 1 > 1$$,解得 $$x > \frac{2}{3}$$,选项 A 正确。
4. 函数 $$y = a^{x-2} - \frac{1}{2}$$ 的图像恒过定点 $$A$$,当 $$x-2 = 0$$ 时,$$y = 1 - \frac{1}{2} = \frac{1}{2}$$,即 $$A(2, \frac{1}{2})$$。代入幂函数 $$y = x^a$$ 得 $$\frac{1}{2} = 2^a$$,解得 $$a = -1$$。幂函数为 $$y = x^{-1}$$,其单调递减区间为 $$(-\infty, 0)$$ 和 $$(0, +\infty)$$,选项 C 正确。
5. 函数 $$y = a^{x-2} + 3$$ 的图像恒过定点 $$P$$,当 $$x-2 = 0$$ 时,$$y = 1 + 3 = 4$$,即 $$P(2, 4)$$。设幂函数为 $$y = x^k$$,代入得 $$4 = 2^k$$,解得 $$k = 2$$。因此 $$f(x) = x^2$$,则 $$f\left( \frac{1}{3} \right) = \left( \frac{1}{3} \right)^2 = \frac{1}{9}$$,选项 A 正确。
6. 根据题意,$$f(0) = 0$$,$$f(1) = 1$$,且 $$f\left( \frac{x}{5} \right) = \frac{1}{2} f(x)$$。递推得 $$f\left( \frac{1}{5} \right) = \frac{1}{2}$$,$$f\left( \frac{1}{25} \right) = \frac{1}{4}$$,$$f\left( \frac{1}{125} \right) = \frac{1}{8}$$,$$f\left( \frac{1}{625} \right) = \frac{1}{16}$$,$$f\left( \frac{1}{3125} \right) = \frac{1}{32}$$,$$f\left( \frac{1}{15625} \right) = \frac{1}{64}$$。由于 $$\frac{1}{2018}$$ 介于 $$\frac{1}{3125}$$ 和 $$\frac{1}{15625}$$ 之间,且函数单调递增,故 $$f\left( \frac{1}{2018} \right) = \frac{1}{64}$$,选项 A 正确。
7. 函数 $$f(x) = \frac{x-1}{a}$$ 的反函数为 $$f^{-1}(x) = a x + 1$$。函数 $$y = a^{|x-1|}$$ 的图像在 $$x = 1$$ 处取得最小值 1,且对称。选项 C 中,反函数为直线,且 $$y = a^{|x-1|}$$ 的图像符合条件,选项 C 正确。
8. 函数 $$f(x) = a^x + b - 1$$ 的图像不经过第三象限,说明 $$f(0) \geq 0$$,即 $$1 + b - 1 \geq 0$$,得 $$b \geq 0$$。图像经过第一、二、四象限,说明 $$a^x$$ 增长缓慢,即 $$0 < a < 1$$,且 $$b > 0$$,选项 A 正确。
9. 函数 $$f(x) = a^x + \log_a(x+1) + 1$$ 恒过定点,当 $$x = 0$$ 时,$$f(0) = 1 + 0 + 1 = 2$$,所以定点为 $$(0, 2)$$,选项 B 正确。
10. 函数 $$y = a^{x-1} + 1$$ 的图像恒过定点,当 $$x-1 = 0$$ 时,$$y = 1 + 1 = 2$$,即 $$(1, 2)$$,选项 D 正确。
.jpg)