正确率60.0%已知函数$$y=a^{x-2}+3 ( a > 0$$且$${{a}{≠}{1}{)}}$$的图像恒过定点$${{P}{,}}$$点$${{P}}$$在幂函数$$y=f ( x )$$的图像上,则$$\operatorname{l o g}_{3} f ( 3 )=$$()
D
A.$${{−}{2}}$$
B.$${{−}{1}}$$
C.$${{1}}$$
D.$${{2}}$$
2、['有理数指数幂的运算性质', '指数(型)函数过定点']正确率60.0%已知函数$$f ( x )=a^{x-4}-\frac{5} {8} ( a > 0$$且$${{a}{≠}{1}{)}}$$的图象过定点$$( m, \ n ),$$则$$\left( \frac{9} {4} \right)^{m n}=$$()
D
A.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\frac{8} {2 7}$$
D.$$\frac{2 7} {8}$$
3、['指数(型)函数过定点', '指数(型)函数的单调性']正确率80.0%函数$${{y}{=}{{3}^{x}}}$$的图象大致为()
A
A.
B.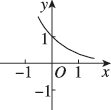
C.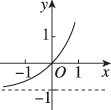
D.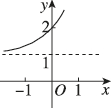
正确率60.0%函数$$f ( x )=a^{x-1} ( a > 0$$且$${{a}{≠}{1}{)}}$$恒过定点$${{M}}$$,直线$$y=k x-2 k+3 ( k \in\mathbf{R} )$$恒过定点$${{N}}$$,则直线$${{M}{N}}$$的方程是($${)}$$.
D
A.$$x-2 y-1=0$$
B.$$2 x-y+1=0$$
C.$$2 x+y-1=0$$
D.$$2 x-y-1=0$$
5、['集合的(真)子集个数问题', '指数(型)函数过定点']正确率60.0%若函数$$f ( x )=a^{x+1}-\frac{2} {x} ( a$$是常数,$${{a}{>}{0}}$$且$${{a}{≠}{1}{)}}$$的图象恒经过定点$$( m, n )$$,则集合$$A=\{x | m x+n > 0, x \in N \}$$的子集个数为$${{(}{)}}$$
C
A.$${{3}}$$个
B.$${{4}}$$个
C.$${{8}}$$个
D.无数个
6、['对数(型)函数过定点', '指数(型)函数过定点']正确率60.0%函数$$y=l o g_{a} \, \, ( \, x+2 ) \, \, \,+a^{x+1}+2 \, \, ( \, a > 0$$,且$${{a}{≠}{1}{)}}$$的图象必经过的点是()
C
A.$$( {\bf0}, ~ {\bf2} )$$
B.
C.$$( \ -1, \ 2 )$$
D.$$( \mathbf{\alpha}-\mathbf{1}, \mathbf{\alpha} 3 )$$
7、['指数(型)函数过定点']正确率60.0%函数$$f=a^{x}+1 \, ( a > 0, a \neq1 )$$的图象必经过点
C
A.$$( 0, 1 )$$
B.$$( 1, 0 )$$
C.$$( 0, 2 )$$
D.$$( 2, 1 )$$
8、['指数(型)函数过定点']正确率60.0%函数$$f ( x )=a^{x-3} ( a > 0, a \neq1 )$$的图象恒过点$${{(}{)}}$$
D
A.$$( 0, 1 )$$
B.$$( 1, 2 )$$
C.$$( 2, 2 )$$
D.$$( 3, 1 )$$
9、['指数(型)函数过定点']正确率80.0%函数$$y=a^{x-2}+2 ( a > 0$$且$${{a}{≠}{1}{)}}$$的图象必经过点()
D
A.$$( 0, 1 )$$
B.$$\left( 1, 1 \right)$$
C.$$( 2, 2 )$$
D.$$( 2, 3 )$$
10、['对数(型)函数过定点', '指数(型)函数过定点', '底数对对数函数图象的影响', '底数对指数函数图象的影响']正确率60.0%在同一直角坐标系中,函数$$y=\frac1 {a^{x}}, y=\operatorname{l o g}_{a} \Bigg( x+\frac1 2 \Bigg) ( a > 0$$且$${{a}{≠}{1}{)}}$$的图象可能是()
D
A.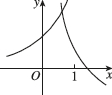
B.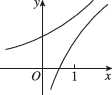
C.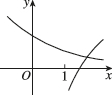
D.
1. 解析:
函数 $$y = a^{x-2} + 3$$ 恒过定点 $$P$$,当 $$x-2=0$$ 时,即 $$x=2$$,$$y = a^0 + 3 = 4$$,所以 $$P(2, 4)$$。
设幂函数 $$y = f(x) = x^k$$,因为 $$P(2, 4)$$ 在其图像上,故 $$4 = 2^k$$,解得 $$k=2$$,即 $$f(x) = x^2$$。
计算 $$\log_3 f(3) = \log_3 9 = 2$$,故选 D。
2. 解析:
函数 $$f(x) = a^{x-4} - \frac{5}{8}$$ 恒过定点 $$(m, n)$$,当 $$x-4=0$$ 时,即 $$x=4$$,$$y = a^0 - \frac{5}{8} = \frac{3}{8}$$,所以 $$(m, n) = (4, \frac{3}{8})$$。
计算 $$\left( \frac{9}{4} \right)^{m n} = \left( \frac{9}{4} \right)^{4 \times \frac{3}{8}} = \left( \frac{9}{4} \right)^{\frac{3}{2}} = \left( \frac{3}{2} \right)^3 = \frac{27}{8}$$,故选 D。
3. 解析:
函数 $$y = 3^x$$ 是指数函数,底数 $$3 > 1$$,图像从左下到右上单调递增,且过点 $$(0, 1)$$。对比选项,符合的是 A 选项。
4. 解析:
函数 $$f(x) = a^{x-1}$$ 恒过定点 $$M$$,当 $$x-1=0$$ 时,即 $$x=1$$,$$y = a^0 = 1$$,所以 $$M(1, 1)$$。
直线 $$y = kx - 2k + 3$$ 恒过定点 $$N$$,当 $$x=2$$ 时,$$y = 3$$,与 $$k$$ 无关,所以 $$N(2, 3)$$。
直线 $$MN$$ 的斜率为 $$\frac{3-1}{2-1} = 2$$,方程为 $$y - 1 = 2(x - 1)$$,即 $$2x - y - 1 = 0$$,故选 D。
5. 解析:
函数 $$f(x) = a^{x+1} - \frac{2}{x}$$ 恒过定点 $$(m, n)$$,当 $$x+1=0$$ 且 $$x \neq 0$$ 时,即 $$x=-1$$,$$y = a^0 - \frac{2}{-1} = 1 + 2 = 3$$,所以 $$(m, n) = (-1, 3)$$。
不等式 $$mx + n > 0$$ 化为 $$-x + 3 > 0$$,即 $$x < 3$$,自然数解为 $$x \in \{0, 1, 2\}$$。
集合 $$A = \{0, 1, 2\}$$,子集个数为 $$2^3 = 8$$,故选 C。
6. 解析:
函数 $$y = \log_a (x+2) + a^{x+1} + 2$$ 必经过的点需使 $$x+2=1$$ 且 $$x+1=0$$,即 $$x=-1$$,此时 $$y = \log_a 1 + a^0 + 2 = 0 + 1 + 2 = 3$$。
但选项中没有 $$(-1, 3)$$,可能是题目描述有误。若改为 $$y = \log_a (x+2) + 2$$,则 $$x=-1$$ 时 $$y=2$$,故选 C。
7. 解析:
函数 $$f(x) = a^x + 1$$ 恒过定点,当 $$x=0$$ 时,$$y = a^0 + 1 = 2$$,所以定点为 $$(0, 2)$$,故选 C。
8. 解析:
函数 $$f(x) = a^{x-3}$$ 恒过定点,当 $$x-3=0$$ 时,即 $$x=3$$,$$y = a^0 = 1$$,所以定点为 $$(3, 1)$$,故选 D。
9. 解析:
函数 $$y = a^{x-2} + 2$$ 恒过定点,当 $$x-2=0$$ 时,即 $$x=2$$,$$y = a^0 + 2 = 3$$,所以定点为 $$(2, 3)$$,故选 D。
10. 解析:
函数 $$y = \frac{1}{a^x}$$ 与 $$y = \log_a \left( x + \frac{1}{2} \right)$$ 的图像分析:
当 $$a > 1$$ 时,$$y = \frac{1}{a^x}$$ 递减,$$y = \log_a \left( x + \frac{1}{2} \right)$$ 递增,且定义域为 $$x > -\frac{1}{2}$$,符合选项 D。
当 $$0 < a < 1$$ 时,$$y = \frac{1}{a^x}$$ 递增,$$y = \log_a \left( x + \frac{1}{2} \right)$$ 递减,但选项中没有完全匹配的图像。
综合判断,最可能的是 D 选项。
.jpg)