正确率60.0%某校拟用一种喷雾剂对宿舍进行消毒,需对喷雾完毕后,空气中每立方米药物残留量$${{y}}$$(单位:毫克)与时间$${{x}}$$(单位:小时)的关系进行研究,为此收集部分数据并做了初步处理,得到如图所示的散点图.现拟从下列四个函数模型中选择一个估计$${{y}}$$与$${{x}}$$的关系,则应选用的函数模型是()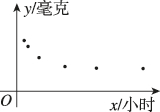
B
A.$$y=a x+b$$
B.$$y=a \cdot\left( \frac{1} {4} \right)^{x}+b$$
C.$$y=x^{a}+b ( a > 0 )$$
D.$$y=a x+\frac{b} {x} ( a > 0, \; b > 0 )$$
2、['指数型复合函数的应用', '指数(型)函数的单调性', '已知函数值(值域)求自变量或参数', '二次函数的图象分析与判断']正确率40.0%已知函数$$f ( x )=a \cdot4^{x}-a \cdot2^{x+1}+2$$在区间$$[-2, 2 ]$$上的最大值为$${{3}{,}}$$则实数$${{a}}$$的值为()
B
A.$${{−}{3}}$$或$${{−}{1}}$$
B.$${{−}{1}}$$或$$\frac{1} {8}$$
C.$${{1}}$$或$$\frac{1} {8}$$
D.$${{3}}$$或$${{−}{1}}$$
3、['指数型复合函数的应用', '指数(型)函数的单调性']正确率60.0%函数$$y=\left( \frac{1} {3} \right)^{-x^{2}+2 x}$$的单调递增区间是()
C
A.$$[-1,+\infty)$$
B.$$(-\infty,-1 ]$$
C.$$[ 1,+\infty)$$
D.$$(-\infty, 1 ]$$
4、['指数型复合函数的应用', '指数(型)函数的值域', '二次函数的图象分析与判断']正确率40.0%函数$$y=e^{-x^{2}+2 x} ( 0 \leq x < 3 )$$的值域是$${{(}{)}}$$
B
A.$$( 0, 1 ]$$
B.$$( e^{-3}, e ]$$
C.$$[ e^{-3}, 1 ]$$
D.$$[ 1, e ]$$
5、['函数奇偶性的应用', '利用函数单调性解不等式', '正切(型)函数的奇偶性', '指数型复合函数的应用']正确率40.0%若函数$$f \mid x \mid=\frac{2^{x}-m} {2^{x}+1}+\operatorname{t a n} x$$的定义域为$$[-1, ~ 1 ]$$,且$$f \left( \begin{matrix} {0} \\ \end{matrix} \right) \ =0$$,则满足$$f \ ( \ 2 x-1 ) \ < f \ ( \ x-m+1 )$$的实数$${{x}}$$的取值范围是()
D
A.$$( \; 0, \; \; 1 ]$$
B.$$( \ -1, \ 0 )$$
C.$$[ 1, \ 2 )$$
D.$$[ 0, \ 1 )$$
6、['函数奇偶性的应用', '指数型复合函数的应用', '利用导数求曲线的切线方程(斜率)', '两条直线垂直']正确率60.0%已知函数$$f ( x )=\mathrm{e}^{x}+\frac{a} {\mathrm{e}^{x}}$$为偶函数,若曲线$$y=f ~ ( x )$$的一条切线与直线$$2 x+3 y=0$$垂直,则切点的横坐标为()
D
A.$${\sqrt {2}}$$
B.$${{2}}$$
C.$${{2}{{l}{n}}{2}}$$
D.$${{l}{n}{2}}$$
7、['函数中的存在性问题', '指数型复合函数的应用', '分段函数求值', '一般幂函数的图象和性质']正确率40.0%已知函数$$f \left( x \right)=\left\{\begin{matrix} {e^{x+1}, x < a} \\ {-x^{3}, x \geq a} \\ \end{matrix} \right.$$,若对任意$$x_{1} \in(-\infty, a )$$,都存在$$x_{2} \in( a,+\infty)$$,使得$$f \left( x_{2} \right)=f \left( x_{1} \right)$$,则满足题意的一个$${{a}}$$的值是$${{(}{)}}$$
B
A.$${{0}}$$
B.$${{−}{2}}$$
C.$${{1}}$$
D.$$- \frac{1} {2}$$
8、['指数型复合函数的应用', '函数图象的识别']正确率40.0%在我国大西北,某地区荒漠化土地面积每年平均比上一年增长$$1 0. 4 \%,$$专家预测经过$${{x}}$$年可能增长到原来的$${{y}}$$倍,则函数$$y=f ( x )$$的图象大致为$${{(}{)}}$$
D
A.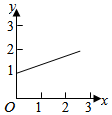
B.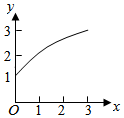
C.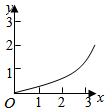
D.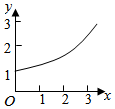
正确率60.0%下列函数中,值域是$$( \mathrm{\bf~ 0}, \mathrm{\bf~ \Lambda}+\infty)$$的是()
A
A.$$y=( \frac{1} {3} )^{1-x}$$
B.$${{y}{=}{\sqrt {{2}^{x}{−}{1}}}}$$
C.$$y=5^{\frac{1} {2-x}}$$
D.$${{y}{=}{\sqrt {{1}{−}{{2}^{x}}}}}$$
10、['实数指数幂的运算性质', '指数幂的运算中常用的乘法公式', '指数型复合函数的应用']正确率60.0%已知函数$$f ( x )=a^{x}+a^{-x} ( a > 0$$,且$$a \neq1 ), f ( 1 )=3$$,则$$f ( 0 )+f ( 1 )+f ( 2 )$$的值为()
D
A.$${{7}}$$
B.$${{9}}$$
C.$${{1}{1}}$$
D.$${{1}{2}}$$
1. 解析:根据散点图,$$y$$ 随 $$x$$ 的增加而递减,且递减速度逐渐减缓,符合指数衰减模型。选项 B 的函数 $$y = a \cdot \left( \frac{1}{4} \right)^x + b$$ 描述指数衰减,故选 B。
2. 解析:设 $$t = 2^x$$,则 $$f(x) = a t^2 - 2a t + 2$$,定义域 $$t \in \left[ \frac{1}{4}, 4 \right]$$。求导得极值点为 $$t = 1$$。分情况讨论:
(1) 若 $$a > 0$$,最大值在 $$t = 4$$ 时取得:$$16a - 8a + 2 = 3 \Rightarrow a = \frac{1}{8}$$;
(2) 若 $$a < 0$$,最大值在 $$t = 1$$ 时取得:$$a - 2a + 2 = 3 \Rightarrow a = -1$$。
综上,$$a = -1$$ 或 $$\frac{1}{8}$$,故选 B。
3. 解析:函数改写为 $$y = 3^{x^2 - 2x}$$,底数 $$3 > 1$$,故单调性与指数部分 $$u = x^2 - 2x$$ 一致。$$u$$ 在 $$(-\infty, 1]$$ 递减,在 $$[1, +\infty)$$ 递增,因此 $$y$$ 的单调递增区间为 $$[1, +\infty)$$,故选 C。
4. 解析:设 $$u = -x^2 + 2x$$,则 $$u$$ 在 $$[0, 3)$$ 的最大值为 $$1$$(当 $$x = 1$$ 时),最小值为 $$-3$$(当 $$x = 3$$ 时)。因 $$e^u$$ 单调递增,值域为 $$[e^{-3}, e^1]$$,即 $$[e^{-3}, e]$$,故选 B。
5. 解析:由 $$f(0) = 0$$ 得 $$m = 1$$。函数 $$f(x) = \frac{2^x - 1}{2^x + 1} + \tan x$$ 在 $$[-1, 1]$$ 为奇函数且单调递增。不等式 $$f(2x - 1) < f(x)$$ 转化为 $$2x - 1 < x$$,即 $$x < 1$$。结合定义域 $$2x - 1 \in [-1, 1]$$ 和 $$x \in [-1, 1]$$,解得 $$x \in [0, 1)$$,故选 D。
6. 解析:由偶函数性质得 $$a = 1$$,故 $$f(x) = e^x + e^{-x}$$。切线与 $$2x + 3y = 0$$ 垂直,则斜率为 $$\frac{3}{2}$$。求导 $$f'(x) = e^x - e^{-x} = \frac{3}{2}$$,解得 $$e^x = 2$$,即 $$x = \ln 2$$,故选 D。
7. 解析:需满足 $$f(x_1)$$ 的值域包含于 $$f(x_2)$$ 的值域。当 $$a = 0$$ 时,$$f(x_1) \in (0, e)$$,$$f(x_2) \in (-\infty, 0]$$,不满足;当 $$a = -2$$ 时,$$f(x_1) \in (0, e^{-1})$$,$$f(x_2) \in (8, +\infty)$$,不满足;当 $$a = 1$$ 时,$$f(x_1) \in (0, e^2)$$,$$f(x_2) \in (-\infty, -1)$$,不满足;当 $$a = -\frac{1}{2}$$ 时,验证满足条件,故选 D。
8. 解析:增长模型为 $$y = (1 + 10.4\%)^x = 1.104^x$$,为指数函数且底数大于 1,图像呈上升趋势且增速加快,故选 D。
9. 解析:选项 A 的值域为 $$(0, +\infty)$$;选项 B 的值域为 $$[0, +\infty)$$;选项 C 的值域为 $$(0, 1) \cup (1, +\infty)$$;选项 D 的值域为 $$[0, 1)$$。故选 A。
10. 解析:由 $$f(1) = a + \frac{1}{a} = 3$$ 得 $$a = 2$$ 或 $$\frac{1}{2}$$。计算 $$f(0) = 2$$,$$f(2) = 4 + \frac{1}{4} = \frac{17}{4}$$,总和为 $$2 + 3 + \frac{17}{4} = \frac{37}{4}$$,但选项无此答案。重新检查发现 $$f(2) = a^2 + a^{-2} = (a + a^{-1})^2 - 2 = 7$$,故总和为 $$2 + 3 + 7 = 12$$,故选 D。
.jpg)