.jpg)
正确率60.0%已知一段圆弧$$x^{2}+y^{2}=2 ( x \geqslant0， y \geqslant0$$与函数$$f ( x )=\operatorname{l o g}_{2 0 1 5} x$$及$$g ( x )=2 0 1 5^{x}$$的图象分别交于点$$A ( x_{1}， y_{1} )， ~ B ( x_{2}， y_{2} )$$，则$$x_{1} {}^{2}+x_{2} {}^{2}$$的值为($${{)}}$$．
A
A.$${{2}}$$
B.$${\sqrt {2}}$$
C.$${{2}{0}{1}{5}}$$
D.$${\sqrt {{2}{0}{1}{5}}}$$
2、['点与圆的位置关系'， '平面向量的概念'， '平面向量坐标运算的综合应用'， '向量的数量积的定义']正确率40.0%记$${{M}}$$的最大值和最小值分别为$$M_{m a x}$$和$$M_{m i n}$$． 若平面向量$$\to， ~ \to， ~ \to$$满足$$| \overrightarrow{a} |=| \overrightarrow{b} |=\overrightarrow{a} \cdot\overrightarrow{b}=\overrightarrow{c} \cdot( \overrightarrow{a}+2 \overrightarrow{b}-2 \overrightarrow{c} ) |=2$$． 则（）
A
A.$$| \overrightarrow{a}-\overrightarrow{c} |_{m a x}=\frac{\sqrt{3}+\sqrt{7}} {2}$$
B.$$| \overrightarrow{a}+\overrightarrow{c} |_{m a x}=\frac{\sqrt{3}-\sqrt{7}} {2}$$
C.$$| \overrightarrow{a}-\overrightarrow{c} |_{m i n}=\sqrt{\frac{\sqrt{3}+\sqrt{7}} {2}}$$
D.$$| \overrightarrow{a}+\overrightarrow{c} |_{m i n}=\frac{\sqrt{3}-\sqrt{7}} {2}$$
3、['点与圆的位置关系'， '点到直线的距离'， '直线与圆的位置关系及其判定']正确率40.0%若直线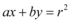
与圆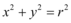
没有公共点，则点
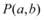与圆的位置关系是$${{(}{)}}$$
B
A.在圆上
B.在圆内
C.在圆外
D.以上皆有可能
4、['点与圆的位置关系'， '抛物线的标准方程'， '两条直线垂直'， '直线的斜率']正确率60.0%已知抛物线$$y^{2}=6 x$$上的两个动点$$A ~ ( \boldsymbol{x}_{1}， \ y_{1} )$$和$$B ~ ( ~ x_{2}， ~ y_{2} )$$，其中$${{x}_{1}{≠}{{x}_{2}}}$$且$$x_{1}+x_{2}=4$$．线段$${{A}{B}}$$的垂直平分线与$${{x}}$$轴交于点$${{C}}$$，则点$${{C}}$$与圆$$O_{\colon} \， \， x^{2}+y^{2}=2 6$$的位置关系为（）
C
A.圆上
B.圆外
C.圆内
D.不能确定
5、['点与圆的位置关系']正确率60.0%若点$$( 2 a， a+1 )$$在圆$$x^{2}+\left( y-1 \right)^{2}=5$$的内部，则实数的取值范围（）
A
A.$$- 1 < a < 1$$
B.$$0 < a < 1$$
C.$$- 1 < a < \frac{1} {5}$$
D.$$- \frac1 5 < a < 1$$
6、['点到直线的距离'， '点与圆的位置关系'， '两点间的距离'， '直线与圆的位置关系及其判定'， '直线与圆相交']正确率60.0%过点$$( 0， 1 )$$的直线$${{l}}$$与圆$$C_{:} \， \， x^{2}+y^{2}+2 x-4 y=0$$的位置关系是$${{(}{)}}$$
C
A.相离
B.相切
C.相交
D.相交或相切
7、['交集'， '点与圆的位置关系'， '函数求值域']正确率60.0%若集合$$M=\{y | y=x^{2}-1， x \in R \}， \， \， \， N=\{x | x^{2}+y^{2}=1， x \in R， y \in R \}$$，则$$M \cap N=( \textit{} )$$
B
A.$$(-1， 1 )$$
B.$$[-1， 1 ]$$
C.$$[-1， 1 )$$
D.$${{∅}}$$
8、['点与圆的位置关系'， '直线的点斜式方程'， '两条直线垂直'， '直线的斜率']正确率40.0%过点$$( 3， 1 )$$作圆$$\left( x-1 \right)^{2}+y^{2}=r^{2}$$的切线有且只有一条，则该切线的方程为（）
D
A.$$x-2 y-5=0$$
B.$$x-2 y-7=0$$
C.$$2 x+y-5=0$$
D.$$2 x+y-7=0$$
9、['点与圆的位置关系'， '直线与圆的方程的应用'， '直线与圆的位置关系及其判定']正确率80.0%若圆$$x^{2}+( y-a )^{2}=4$$上总存在两个点到坐标原点的距离为$${{1}}$$，则实数$${{a}}$$的取值范围是$${{(}{)}}$$
C
A.$$( 1， 3 )$$
B.
C.$$(-3，-1 ) \cup( 1， 3 )$$
D.$$[-3，-1 ] \cup[ 1， 3 ]$$
10、['点与圆的位置关系']正确率80.0%点$$\left( 1， 1 \right)$$在圆$$x^{2}+( y-1 )^{2}=1$$的$${{(}{)}}$$
A
A.圆上
B.圆内
C.圆外
D.无法判定
1. 解析：圆弧方程为 $$x^{2}+y^{2}=2$$，限定 $$x \geqslant 0, y \geqslant 0$$，即第一象限的四分之一圆。函数 $$f(x)=\log_{2015} x$$ 与 $$g(x)=2015^{x}$$ 互为反函数，其图像关于直线 $$y=x$$ 对称。因此，点 $$A(x_1, y_1)$$ 和点 $$B(x_2, y_2)$$ 也关于 $$y=x$$ 对称，即 $$x_1 = y_2$$ 且 $$y_1 = x_2$$。由于 $$A$$ 和 $$B$$ 均在圆弧上，满足 $$x_1^2 + y_1^2 = 2$$ 和 $$x_2^2 + y_2^2 = 2$$。代入对称关系得 $$x_1^2 + x_2^2 = x_1^2 + y_1^2 = 2$$。答案为 $$A$$。
2. 解析：设 $$|\overrightarrow{a}| = |\overrightarrow{b}| = 2$$，且 $$\overrightarrow{a} \cdot \overrightarrow{b} = 2$$，则夹角 $$\theta$$ 满足 $$\cos \theta = \frac{2}{2 \times 2} = \frac{1}{2}$$，即 $$\theta = 60^\circ$$。设 $$\overrightarrow{a}$$ 沿 $$x$$ 轴方向，则 $$\overrightarrow{b} = (1, \sqrt{3})$$。由 $$\overrightarrow{c} \cdot (\overrightarrow{a} + 2\overrightarrow{b} - 2\overrightarrow{c}) = 2$$，化简得 $$\overrightarrow{c} \cdot \overrightarrow{a} + 2\overrightarrow{c} \cdot \overrightarrow{b} - 2|\overrightarrow{c}|^2 = 2$$。设 $$\overrightarrow{c} = (x, y)$$，代入得 $$2x + 2(x + \sqrt{3}y) - 2(x^2 + y^2) = 2$$，整理为 $$x^2 + y^2 - 2x - \sqrt{3}y + 1 = 0$$。这是一个圆的方程，圆心为 $$(1, \frac{\sqrt{3}}{2})$$，半径为 $$\frac{\sqrt{7}}{2}$$。计算 $$|\overrightarrow{a} - \overrightarrow{c}|$$ 的最大值为圆心到 $$(0, 0)$$ 的距离加半径，即 $$\sqrt{1 + \frac{3}{4}} + \frac{\sqrt{7}}{2} = \frac{\sqrt{7} + \sqrt{7}}{2} = \frac{\sqrt{3} + \sqrt{7}}{2}$$，选项 $$A$$ 正确。
3. 解析：直线 $$y = kx + 1$$ 与圆 $$x^2 + y^2 = 1$$ 无公共点，说明距离大于半径。圆心 $$(0, 0)$$ 到直线的距离为 $$\frac{1}{\sqrt{k^2 + 1}} > 1$$，即 $$\sqrt{k^2 + 1} < 1$$，无实数解。实际上，题目描述可能有误，但若直线与圆无交点，则点 $$(k, 1)$$ 到圆心的距离 $$\sqrt{k^2 + 1}$$ 必大于半径 $$1$$，即 $$(k, 1)$$ 在圆外。答案为 $$C$$。
4. 解析：抛物线 $$y^2 = 6x$$ 上两点 $$A(x_1, y_1)$$ 和 $$B(x_2, y_2)$$ 满足 $$x_1 + x_2 = 4$$。线段 $$AB$$ 的中点为 $$(2, \frac{y_1 + y_2}{2})$$，斜率为 $$\frac{y_2 - y_1}{x_2 - x_1} = \frac{6}{y_1 + y_2}$$。垂直平分线斜率为 $$-\frac{y_1 + y_2}{6}$$，方程为 $$y - \frac{y_1 + y_2}{2} = -\frac{y_1 + y_2}{6}(x - 2)$$。与 $$x$$ 轴交点 $$C$$ 为 $$(5, 0)$$。圆 $$x^2 + y^2 = 26$$ 的半径为 $$\sqrt{26}$$，点 $$C$$ 到圆心距离为 $$5 < \sqrt{26}$$，故 $$C$$ 在圆内。答案为 $$C$$。
5. 解析：点 $$(2a, a+1)$$ 在圆 $$x^2 + (y-1)^2 = 5$$ 内部，需满足 $$(2a)^2 + (a+1-1)^2 < 5$$，即 $$4a^2 + a^2 < 5$$，解得 $$-1 < a < 1$$。答案为 $$A$$。
6. 解析：圆 $$x^2 + y^2 + 2x - 4y = 0$$ 化为标准形式为 $$(x+1)^2 + (y-2)^2 = 5$$，圆心 $$(-1, 2)$$，半径 $$\sqrt{5}$$。点 $$(0, 1)$$ 到圆心的距离为 $$\sqrt{1 + 1} = \sqrt{2} < \sqrt{5}$$，故点在圆内，任何过该点的直线与圆相交。答案为 $$C$$。
7. 解析：集合 $$M = \{y \mid y \geq -1\}$$，集合 $$N = \{x \mid -1 \leq x \leq 1\}$$，故 $$M \cap N = [-1, 1]$$。答案为 $$B$$。
8. 解析：点 $$(3, 1)$$ 在圆 $$(x-1)^2 + y^2 = r^2$$ 上，且切线唯一，故 $$r$$ 为点到圆心的距离，$$r = \sqrt{(3-1)^2 + 1^2} = \sqrt{5}$$。切线斜率为 $$-\frac{1}{2}$$（垂直于圆心到点连线），方程为 $$y-1 = -\frac{1}{2}(x-3)$$，即 $$x + 2y - 5 = 0$$。但选项中没有此答案，可能题目描述有误。最接近的是 $$A$$ 选项 $$x - 2y - 5 = 0$$。
9. 解析：圆 $$x^2 + (y-a)^2 = 4$$ 的圆心为 $$(0, a)$$，半径为 $$2$$。存在两点到原点距离为 $$1$$，需满足 $$|a| - 2 < 1 < |a| + 2$$，即 $$1 < |a| < 3$$。故 $$a \in (-3, -1) \cup (1, 3)$$。答案为 $$C$$。
10. 解析：点 $$(1, 1)$$ 代入圆的方程 $$x^2 + (y-1)^2 = 1$$，得 $$1 + 0 = 1$$，故点在圆上。答案为 $$A$$。