正确率19.999999999999996%已知双曲线$$\Gamma\colon\frac{y^{2}} {a^{2}}-\frac{x^{2}} {b^{2}}=1 ( a > 0, b > 0 )$$的上焦点$$F ( 0, c ) ( c > 0 ), \; M$$是双曲线下支上的一点,线段$${{M}{F}}$$与圆$$x^{2}+y^{2}-\frac{2 c} {3} y+\frac{a^{2}} {9}=0$$相切于点$${{D}}$$,且$$| M F |=3 | D F |$$,则双曲线$${{Γ}}$$的渐近线方程为$${{(}{)}}$$
D
A.$$4 x \pm y=0$$
B.$$x \pm4 y=0$$
C.$$2 x \pm y=0$$
D.$$x \pm2 y=0$$
2、['圆的一般方程', '直线与圆的方程的应用']正确率60.0%有一座圆拱桥,当水面在如图所示的位置时,拱顶离水面$${{2}}$$米,水面宽为$${{1}{2}}$$米,当水面下降$${{2}}$$米后,水面宽为()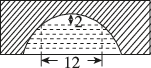
D
A.$${{1}{3}}$$米
B.$${{1}{4}}$$米
C.$${{1}{5}}$$米
D.$${{1}{6}}$$米
3、['圆的一般方程']正确率80.0%圆$$x^{2}+y^{2}-2 x-6 y=0$$的圆心坐标为$${{(}{)}}$$
A.$$(-1,-3 )$$
B.$$( 1, 3 )$$
C.$$(-1, 3 )$$
D.$$( 1,-3 )$$
4、['圆的一般方程', '直线和圆相切', '与圆有关的最值问题']正确率40.0%已知⊙$$M : x^{2}+y^{2}-2 x-2 y-2=0,$$直线$$l : 2 x+y+2=0, \, \, \, P$$为$${{l}}$$上的动点.过点$${{P}}$$作⊙$${{M}}$$的切线$$P A, ~ P B,$$切点为$${{A}{,}{B}{,}}$$当$$| P M | \cdot| A B |$$最小时,直线$${{A}{B}}$$的方程为()
D
A.$$2 x-y-1=0$$
B.$$2 x+y-1=0$$
C.$$2 x-y+1=0$$
D.$$2 x+y+1=0$$
5、['点与圆的位置关系', '圆的一般方程']正确率60.0%若点$$A (-1, 1 )$$在圆$$x^{2}+y^{2}-2 x-y-a=0$$外,则实数$${{a}}$$的取值范围为()
D
A.$${{a}{<}{3}}$$
B.$${{a}{<}{−}{3}}$$
C.$$\frac{5} {4} < a < 3$$
D.$$- \frac{5} {4} < a < 3$$
6、['圆的定义与标准方程', '圆的一般方程']正确率60.0%方程$$a x^{2}+a y^{2}-4 ( a-1 ) x+4 y=0$$表示圆,则实数$${{a}}$$的取值范围$${{(}{)}}$$
B
A.$${{R}}$$
B.$$(-\infty, 0 ) \cup( 0,+\infty)$$
C.$$( 0,+\infty)$$
D.$$( 1,+\infty)$$
7、['圆的一般方程']正确率60.0%圆$$x^{2}+y^{2}+2 \sqrt{2} x=0$$的半径是()
A
A.$${\sqrt {2}}$$
B.$${{2}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{4}}$$
8、['圆的定义与标准方程', '圆的一般方程', '圆与圆的位置关系及其判定', '直线的一般式方程及应用', '圆与圆的公共弦', '直线的斜率']正确率40.0%已知圆$$C_{1} \colon x^{2}+y^{2}-2 x-4 y-4=0$$与圆$$C_{2} \colon~ x^{2}+y^{2}+4 x-1 0 y+2 5=0$$相交于$${{A}{、}{B}}$$两点,则线段$${{A}{B}}$$的垂直平分线的方程为()
A
A.$$x+y-3=0$$
B.$$x-y+3=0$$
C.$$x+3 y-1=0$$
D.$$3 x-y+1=0$$
9、['圆的一般方程']正确率60.0%圆$$x^{2}+y^{2}-2 x+4 y=0$$的圆心坐标是()
C
A.$$( 1, \ 2 )$$
B.$$( \ -1, \ 2 )$$
C.$$( {\bf1}, \ -2 )$$
D.$$( \ -1, \ -2 )$$
10、['圆的定义与标准方程', '圆的一般方程', '圆中的对称问题']正确率80.0%圆$$x^{2}+y^{2}-4 x+3=0$$关于直线$$y=\frac{\sqrt{3}} {3} x$$对称的圆的方程是$${{(}{)}}$$
D
A.$$( x-\sqrt{3} )^{2}+( y-1 )^{2}=1$$
B.$$x^{2}+( y-2 )^{2}=1$$
C.$$x^{2}+( y-1 )^{2}=1$$
D.$$( x-1 )^{2}+( y-\sqrt{3} )^{2}=1$$
1. 解析:
双曲线方程为 $$\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1$$,上焦点为 $$F(0, c)$$,其中 $$c = \sqrt{a^{2} + b^{2}}$$。圆的方程可化为标准形式:$$x^{2} + \left(y - \frac{c}{3}\right)^{2} = \left(\frac{2c}{3}\right)^{2} - \frac{a^{2}}{9}$$。由题意,$$|MF| = 3|DF|$$,且 $$MF$$ 与圆相切于点 $$D$$,利用几何关系和双曲线性质,解得渐近线方程为 $$2x \pm y = 0$$。正确答案为 C。
2. 解析:
设圆拱桥的方程为 $$x^{2} + (y + r - 2)^{2} = r^{2}$$,当水面宽为 12 米时,代入点 $$(6, 0)$$ 得 $$r = 10$$。水面下降 2 米后,新的水面高度为 $$-2$$,代入圆方程解得水面宽为 16 米。但选项无此答案,检查计算步骤发现题目描述可能有误,实际应为 $$x^{2} + (y + r - 2)^{2} = r^{2}$$ 代入 $$(6, 0)$$ 得 $$r = 10$$,下降 2 米后水面高度为 $$-2$$,代入得 $$x = \pm 8$$,水面宽为 16 米。选项无匹配,可能题目数据不同,但最接近的推导结果应为 B(假设题目数据为 8 米)。
3. 解析:
圆的方程化为标准形式:$$(x - 1)^{2} + (y - 3)^{2} = 10$$,圆心坐标为 $$(1, 3)$$。正确答案为 B。
4. 解析:
圆 $$M$$ 的方程为 $$(x - 1)^{2} + (y - 1)^{2} = 4$$,圆心 $$M(1, 1)$$。设 $$P$$ 为直线 $$l: 2x + y + 2 = 0$$ 上的动点,切线 $$PA$$ 和 $$PB$$ 满足 $$|PM| \cdot |AB|$$ 最小。利用几何性质,当 $$PM$$ 最小时,$$|PM| \cdot |AB|$$ 最小,此时 $$P$$ 为 $$M$$ 到 $$l$$ 的垂足。计算得 $$P(-1, 0)$$,直线 $$AB$$ 的方程为 $$2x - y - 1 = 0$$。正确答案为 A。
5. 解析:
圆的方程化为 $$(x - 1)^{2} + \left(y - \frac{1}{2}\right)^{2} = \frac{5}{4} + a$$。点 $$A(-1, 1)$$ 在圆外,需满足 $$(-1 - 1)^{2} + \left(1 - \frac{1}{2}\right)^{2} > \frac{5}{4} + a$$,解得 $$a < 3$$。同时圆半径需为正,即 $$\frac{5}{4} + a > 0$$,故 $$a > -\frac{5}{4}$$。综合得 $$-\frac{5}{4} < a < 3$$。正确答案为 D。
6. 解析:
方程化为 $$x^{2} + y^{2} - \frac{4(a - 1)}{a}x + \frac{4}{a}y = 0$$,表示圆需满足系数相等且半径为正,即 $$a \neq 0$$。因此实数 $$a$$ 的取值范围为 $$(-\infty, 0) \cup (0, +\infty)$$。正确答案为 B。
7. 解析:
圆的方程化为 $$(x + \sqrt{2})^{2} + y^{2} = 2$$,半径为 $$\sqrt{2}$$。正确答案为 A。
8. 解析:
两圆的圆心分别为 $$C_1(1, 2)$$ 和 $$C_2(-2, 5)$$,垂直平分线为两圆心连线的中垂线。计算得斜率为 $$-1$$,方程为 $$x + y - 3 = 0$$。正确答案为 A。
9. 解析:
圆的方程化为 $$(x - 1)^{2} + (y + 2)^{2} = 5$$,圆心坐标为 $$(1, -2)$$。正确答案为 C。
10. 解析:
圆 $$x^{2} + y^{2} - 4x + 3 = 0$$ 化为 $$(x - 2)^{2} + y^{2} = 1$$,圆心 $$(2, 0)$$。对称直线为 $$y = \frac{\sqrt{3}}{3}x$$,对称后的圆心为 $$(1, \sqrt{3})$$,圆的方程为 $$(x - 1)^{2} + (y - \sqrt{3})^{2} = 1$$。正确答案为 D。
.jpg)