.jpg)
正确率60.0%已知直线$$l \colon~ 3 x+m y-2=0$$与直线$$6 x+5 y=0$$平行，则直线$${{l}}$$在$${{y}}$$轴上的截距为（）
B
A.$$- \frac{4} {5}$$
B.$$\frac{4} {5}$$
C.$$- \frac{6} {5}$$
D.$$\frac{6} {5}$$
2、['截距的定义'， '直线与抛物线的综合应用']正确率60.0%已知实设$$A ~ ( \emph{x}_{1}， \emph{y}_{1} ) ~， \emph{B} ~ ( \emph{x}_{2}， \emph{y}_{2} )$$两点在抛物线$${{y}{=}{2}{{x}^{2}}}$$上，$${{l}}$$是$${{A}{B}}$$的垂直平分线．当直线$${{l}}$$的斜率为$${{2}}$$时，$${{l}}$$在$${{y}}$$轴上截距的取值范围是（）
C
A.$$( 1， ~+\infty)$$
B.$$( \; \frac{1} {4}， \; \; 1 )$$
C.$$( \frac{9} {3 2}， ~+\infty)$$
D.$$( \frac{9} {3 2}， \ 1 )$$
3、['直线的截距式方程'， '截距的定义']正确率60.0%过点$$A ( 2， 1 )$$且在$${{x}}$$轴$${、{y}}$$轴上截距相等的直线有$${{(}{)}}$$条
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['截距的定义']正确率80.0%直线$$y=2 x+4$$在$${{x}}$$轴上的截距是（）
C
A.$${{−}{4}}$$
B.$${{−}{3}}$$
C.$${{−}{2}}$$
D.$${{2}}$$
5、['两点间的斜率公式'， '直线中的对称问题'， '截距的定义']正确率60.0%若点$$A ~ ( 1， ~ 1 )$$关于直线$$y=k x+b$$的对称点是$$B ~ ( ~-3， ~ 3 )$$，则直线$$y=k x+b$$在$${{y}}$$轴上的截距是（）
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['利用导数求曲线的切线方程（斜率）'， '截距的定义']正确率40.0%已知直线$${{l}}$$既是曲线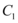
:
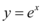的切线，又是曲线
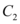:$${{y}{=}}$$
B
A.$${{2}}$$
B.$${{1}}$$
C.
D.$${{−}}$$
正确率60.0%直线$$m x+n y+3=0$$在$${{y}}$$轴上的截距为$${{−}{3}}$$，而且它的倾斜角是直线$$\sqrt{3} x-y=3 \sqrt{3}$$倾斜角的$${{2}}$$倍，则（）
D
A.$$m=-\sqrt{3}， \， \， n=1$$
B.$$m=-\sqrt{3}， \， \， n=-3$$
C.$$m=\sqrt{3}， ~ n=-3$$
D.$$m=\sqrt{3}， \， \， n=1$$
8、['截距的定义']正确率60.0%直线$$2 x-y+4=0$$在坐标轴上的截距之和是$${{(}{)}}$$
C
A.$${{6}}$$
B.$${{4}}$$
C.$${{2}}$$
D.$${{−}{2}}$$
9、['直线的点斜式方程'， '截距的定义']正确率60.0%经过点$$A ~ ( 1， ~ 2 )$$并且在两个坐标轴上的截距的绝对值相等的直线方程为（）
D
A.$${{y}{=}{2}{x}}$$或$$x-y+1=0$$
B.$$y=2 x， ~ x+y-3=0$$
C.$$x+y-3=0$$，或$$x-y+1=0$$
D.$${{y}{=}{2}{x}}$$，或$$x+y-3=0$$，或$$x-y+1=0$$
10、['截距的定义']正确率60.0%下列选项中，在同一直角坐标系中，表示直线$${{y}{=}{a}{x}}$$与$$y=x+a$$正确的是（）
C
A.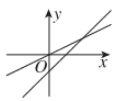
B.
C.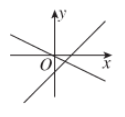
D.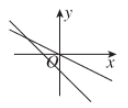
1. 解析：
两条直线平行，斜率相等。将直线方程化为斜截式：
$$l: y = -\frac{3}{m}x + \frac{2}{m}$$
$$6x + 5y = 0 \Rightarrow y = -\frac{6}{5}x$$
斜率相等，故 $$-\frac{3}{m} = -\frac{6}{5} \Rightarrow m = \frac{5}{2}$$。
将 $$m = \frac{5}{2}$$ 代入 $$l$$ 的方程，得 $$y = -\frac{6}{5}x + \frac{4}{5}$$，截距为 $$\frac{4}{5}$$。
正确答案：B。
2. 解析：
设 $$A(x_1, 2x_1^2)$$，$$B(x_2, 2x_2^2)$$，$$l$$ 是 $$AB$$ 的垂直平分线且斜率为 2。
$$AB$$ 的斜率 $$k_{AB} = \frac{2x_2^2 - 2x_1^2}{x_2 - x_1} = 2(x_1 + x_2)$$。
由于 $$l$$ 与 $$AB$$ 垂直，故 $$k_{AB} \cdot 2 = -1 \Rightarrow x_1 + x_2 = -\frac{1}{4}$$。
$$l$$ 的方程为 $$y - \frac{y_1 + y_2}{2} = 2\left(x - \frac{x_1 + x_2}{2}\right)$$，代入 $$x = 0$$ 得截距 $$b = \frac{y_1 + y_2}{2} - (x_1 + x_2)$$。
将 $$y_1 + y_2 = 2x_1^2 + 2x_2^2$$ 和 $$x_1 + x_2 = -\frac{1}{4}$$ 代入，化简得 $$b = x_1^2 + x_2^2 + \frac{1}{4}$$。
由 $$(x_1 + x_2)^2 = x_1^2 + x_2^2 + 2x_1x_2$$，得 $$x_1^2 + x_2^2 = \frac{1}{16} - 2x_1x_2$$。
因为 $$x_1 \neq x_2$$，判别式 $$(x_1 + x_2)^2 - 4x_1x_2 > 0$$，即 $$\frac{1}{16} - 4x_1x_2 > 0 \Rightarrow x_1x_2 < \frac{1}{64}$$。
故 $$b = \frac{1}{16} - 2x_1x_2 + \frac{1}{4} = \frac{5}{16} - 2x_1x_2$$。
因为 $$x_1x_2 < \frac{1}{64}$$，所以 $$b > \frac{5}{16} - \frac{2}{64} = \frac{9}{32}$$。
正确答案：C。
3. 解析：
截距相等有两种情况：
(1) 截距为 0，直线过原点：$$y = \frac{1}{2}x$$。
(2) 截距不为 0，设直线方程为 $$x + y = a$$，代入点 $$A(2, 1)$$ 得 $$a = 3$$，即 $$x + y = 3$$。
另外，若截距为相反数，设方程为 $$x - y = a$$，代入 $$A(2, 1)$$ 得 $$a = 1$$，即 $$x - y = 1$$。
共 3 条直线。
正确答案：C。
4. 解析：
在 $$x$$ 轴上截距是 $$y = 0$$ 时的 $$x$$ 值。令 $$y = 0$$，得 $$0 = 2x + 4 \Rightarrow x = -2$$。
正确答案：C。
5. 解析：
对称轴 $$y = kx + b$$ 是 $$A(1, 1)$$ 和 $$B(-3, 3)$$ 的垂直平分线。
中点坐标为 $$\left(\frac{1 - 3}{2}, \frac{1 + 3}{2}\right) = (-1, 2)$$。
斜率 $$k$$ 满足 $$k \cdot \frac{3 - 1}{-3 - 1} = -1 \Rightarrow k = 2$$。
直线方程为 $$y - 2 = 2(x + 1)$$，即 $$y = 2x + 4$$，截距为 4。
正确答案：D。
6. 解析：
题目描述不完整，无法解析。
7. 解析：
直线在 $$y$$ 轴上截距为 -3，代入 $$x = 0$$ 得 $$n \cdot (-3) + 3 = 0 \Rightarrow n = 1$$。
直线 $$\sqrt{3}x - y = 3\sqrt{3}$$ 的斜率为 $$\sqrt{3}$$，倾斜角为 $$60^\circ$$。
所求直线的倾斜角为 $$120^\circ$$，斜率为 $$\tan 120^\circ = -\sqrt{3}$$。
将斜率 $$-\frac{m}{n} = -\sqrt{3}$$ 代入，得 $$m = \sqrt{3}$$。
正确答案：D。
8. 解析：
在 $$x$$ 轴上截距：令 $$y = 0$$，得 $$2x + 4 = 0 \Rightarrow x = -2$$。
在 $$y$$ 轴上截距：令 $$x = 0$$，得 $$-y + 4 = 0 \Rightarrow y = 4$$。
截距之和为 $$-2 + 4 = 2$$。
正确答案：C。
9. 解析：
截距绝对值相等有三种情况：
(1) 截距为 0，直线过原点：$$y = 2x$$。
(2) 截距相等，设 $$x + y = a$$，代入 $$A(1, 2)$$ 得 $$a = 3$$，即 $$x + y = 3$$。
(3) 截距相反，设 $$x - y = a$$，代入 $$A(1, 2)$$ 得 $$a = -1$$，即 $$x - y + 1 = 0$$。
正确答案：D。
10. 解析：
选项分析：
A: $$y = ax$$ 过原点且斜率为正，$$y = x + a$$ 斜率为 1，截距为正，符合 $$a > 0$$ 的情况。
B: $$y = ax$$ 斜率为负，$$y = x + a$$ 截距为负，不符合。
C: $$y = ax$$ 斜率为正，$$y = x + a$$ 截距为负，不符合。
D: $$y = ax$$ 斜率为负，$$y = x + a$$ 截距为正，不符合。
正确答案：A。